7.28 Divided By 4
renascent
Sep 16, 2025 · 5 min read
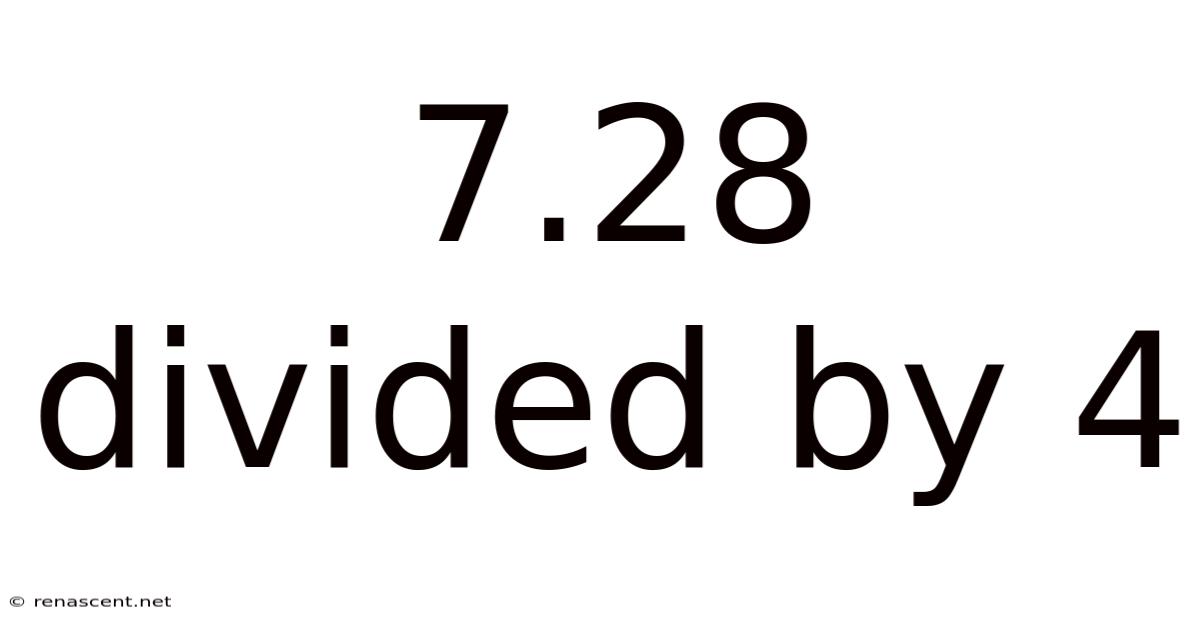
Table of Contents
7.28 Divided by 4: A Deep Dive into Division and Decimal Operations
This article provides a comprehensive explanation of how to solve the division problem 7.28 divided by 4, going beyond a simple answer to explore the underlying mathematical concepts and techniques. We will cover various methods, including long division, using fractions, and understanding the logic behind decimal division. This detailed guide aims to improve your understanding of decimal arithmetic and build your confidence in tackling similar problems.
Introduction: Understanding the Problem
The problem "7.28 divided by 4" asks us to determine how many times the number 4 fits into 7.28. This is a common type of division problem involving decimals, which can seem daunting at first glance. However, by breaking down the process into smaller, manageable steps, we can easily find the solution and gain a deeper understanding of the mathematics involved. This exploration will benefit anyone looking to strengthen their mathematical skills, particularly in the area of decimal arithmetic.
Method 1: Long Division
Long division is a classic method for tackling division problems, especially those involving decimals. Let's work through the problem step-by-step:
-
Set up the problem: Write the problem in the standard long division format:
4 | 7.28 -
Divide the whole number part: How many times does 4 go into 7? It goes once (4 x 1 = 4). Write the 1 above the 7.
1 4 | 7.28 -
Subtract: Subtract 4 from 7, leaving 3.
1 4 | 7.28 4 - 3 -
Bring down the next digit: Bring down the 2, creating the number 32.
1 4 | 7.28 4 - 32 -
Divide again: How many times does 4 go into 32? It goes 8 times (4 x 8 = 32). Write the 8 above the 2.
18 4 | 7.28 4 - 32 -
Subtract: Subtract 32 from 32, leaving 0.
18 4 | 7.28 4 - 32 32 - 0 -
Bring down the final digit: Bring down the 8.
18 4 | 7.28 4 - 32 32 - 08 -
Divide the final digit: How many times does 4 go into 8? It goes 2 times (4 x 2 = 8). Write the 2 above the 8.
1.82 4 | 7.28 4 - 32 32 - 08 08 - 00 -
Final Result: The answer is 1.82.
Method 2: Using Fractions
We can also solve this problem using fractions. Remember that division is the same as multiplying by the reciprocal.
-
Convert the decimal to a fraction: 7.28 can be written as 728/100.
-
Rewrite the division as a fraction: The problem becomes (728/100) ÷ 4.
-
Multiply by the reciprocal of 4: This is equivalent to multiplying by 1/4. So we have (728/100) x (1/4).
-
Simplify: Multiply the numerators (728 x 1 = 728) and the denominators (100 x 4 = 400). This gives us 728/400.
-
Simplify the fraction: We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 4. This gives us 182/100.
-
Convert back to a decimal: 182/100 is equal to 1.82.
Method 3: Understanding Decimal Place Value
A crucial aspect of understanding decimal division is recognizing the place value of each digit. In the number 7.28, the 7 represents 7 ones, the 2 represents 2 tenths (2/10), and the 8 represents 8 hundredths (8/100). When we divide by 4, we are essentially dividing each part of the number by 4.
- Dividing the ones: 7 ÷ 4 = 1 with a remainder of 3.
- Dividing the tenths: The remainder of 3 ones becomes 30 tenths. Adding the 2 tenths, we have 32 tenths. 32 ÷ 4 = 8.
- Dividing the hundredths: We have 8 hundredths. 8 ÷ 4 = 2.
Combining these results, we get 1.82. This method highlights the importance of understanding place value and how it interacts with division operations.
Explanation of the Result: What Does 1.82 Mean?
The answer, 1.82, signifies that if you divide 7.28 into four equal parts, each part will be 1.82 units. This demonstrates the application of division in real-world scenarios such as sharing quantities equally, calculating averages, or determining unit costs.
Frequently Asked Questions (FAQ)
-
Q: What if the division doesn't result in a whole number?
A: Many division problems, particularly those involving decimals, do not result in whole numbers. The remainder is expressed as a decimal or a fraction. The long division method and the fractional method will accurately handle these scenarios.
-
Q: Can I use a calculator?
A: Yes, calculators are a useful tool for performing division, especially for more complex problems. However, it's crucial to understand the underlying mathematical principles to interpret the results correctly and to handle problems where a calculator might not be readily available.
-
Q: Are there other methods to solve this problem?
A: While long division, fractions, and understanding place value are the most common methods, you could also potentially use estimation and iterative processes to approximate the answer. However, the methods outlined above provide more precise and reliable results.
-
Q: How can I improve my skills in decimal division?
A: Practice is key. Work through various problems of increasing difficulty, starting with simpler examples and gradually progressing to more complex ones. Understanding the concepts of place value, fractions, and long division is crucial for mastering decimal division.
Conclusion: Mastering Decimal Division
Understanding how to divide decimals, such as solving 7.28 divided by 4, is a fundamental skill in mathematics. This article has explored multiple methods, including long division, utilizing fractions, and emphasizing the importance of place value. Each method provides a different perspective and helps solidify your understanding of the core mathematical principles involved. By practicing these methods and understanding the logic behind them, you can confidently tackle similar problems and build a strong foundation in decimal arithmetic. The ability to effectively solve such problems is essential not only in academic settings but also in various practical situations requiring precise calculations. Remember, the key to mastery is consistent practice and a thorough grasp of the underlying concepts.
Latest Posts
Latest Posts
-
Braque Houses At L Estaque
Sep 16, 2025
-
135 Pounds In Kilos
Sep 16, 2025
-
What Is Brake Fade
Sep 16, 2025
-
R12 To R134a Conversion
Sep 16, 2025
-
Reality Orientation And Dementia
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 7.28 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.