7 Divided By 98
renascent
Sep 14, 2025 · 5 min read
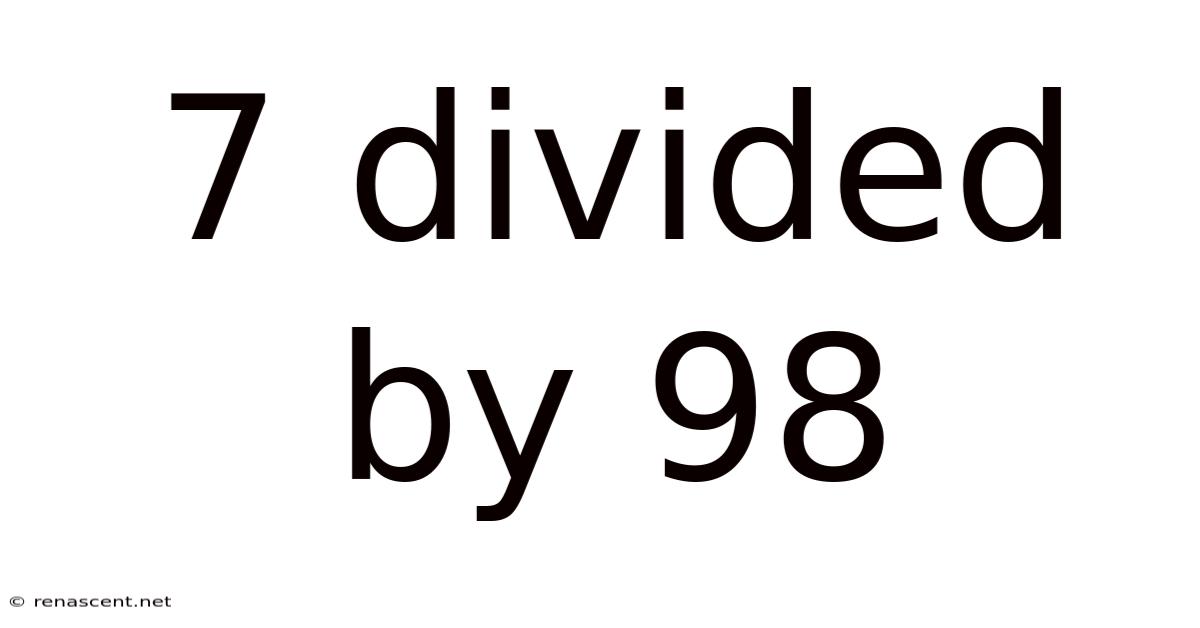
Table of Contents
7 Divided by 98: Unpacking the Concept of Division and Decimal Representation
Dividing 7 by 98 might seem like a simple arithmetic problem, but it offers a rich opportunity to explore several key mathematical concepts, including division, decimals, fractions, and their interconnectedness. This article will not only provide the answer to 7 ÷ 98 but will also delve into the underlying principles, demonstrating how to perform the calculation and interpreting the result in various ways. We'll also address common misconceptions and explore practical applications.
Understanding Division: The Basics
Division is fundamentally the inverse operation of multiplication. When we divide a number (the dividend) by another number (the divisor), we are essentially asking, "How many times does the divisor fit into the dividend?" In the case of 7 ÷ 98, we are asking how many times 98 fits into 7.
Intuitively, we know that 98 is larger than 7, so 98 cannot fit into 7 even once. This leads to a result that is less than 1, which we typically represent as a decimal or a fraction.
Calculating 7 ÷ 98: The Long Division Method
The traditional method for performing division is long division. While calculators offer a quick solution, understanding the process is crucial for grasping the underlying mathematical principles. Let's break down 7 ÷ 98 using long division:
-
Set up the long division: We write 7 as the dividend inside the long division symbol and 98 as the divisor outside.
98 | 7 -
Add a decimal point and zeros: Since 7 is smaller than 98, we add a decimal point after the 7 and append zeros as needed to continue the division.
98 | 7.0000 -
Perform the division: We now try to find how many times 98 goes into 70. It doesn't go in even once, so we write a 0 above the decimal point. Then we consider how many times 98 goes into 700. We can estimate this by dividing 700 by 100 (which is close to 98), resulting in 7. Let's try multiplying 98 by 7: 98 x 7 = 686. We subtract this from 700: 700 - 686 = 14.
0.07 98 | 7.0000 686 --- 14 -
Bring down the next zero: We bring down the next zero to make 140.
0.07 98 | 7.0000 686 --- 140 -
Continue the process: Now we determine how many times 98 goes into 140. It goes in once (98 x 1 = 98). Subtract 98 from 140: 140 - 98 = 42.
0.071 98 | 7.0000 686 --- 140 98 --- 42 -
Repeat: Bring down another zero to make 420. 98 goes into 420 approximately 4 times (98 x 4 = 392). Subtract 392 from 420: 420 - 392 = 28.
0.0714 98 | 7.0000 686 --- 140 98 --- 420 392 --- 28 -
Continue until desired accuracy: We can continue this process, adding zeros and repeating the steps to achieve the desired level of accuracy. The decimal representation of 7 ÷ 98 is a non-terminating decimal (it goes on forever without repeating).
The long division shows us that 7 ÷ 98 is approximately 0.0714...
Representing the Result as a Fraction
Another way to represent the result is as a fraction. The result of 7 ÷ 98 is simply the fraction 7/98. This fraction can be simplified by finding the greatest common divisor (GCD) of 7 and 98. The GCD of 7 and 98 is 7. Therefore, we can simplify the fraction:
7/98 = (7 ÷ 7) / (98 ÷ 7) = 1/14
So, 7 divided by 98 is equivalent to 1/14. This fractional representation provides a concise and exact representation of the result, unlike the decimal approximation which continues infinitely.
Decimal Representation and its Implications
The decimal representation of 7/98 (approximately 0.0714285714...) is a non-terminating, repeating decimal. This means it continues infinitely without ever ending or settling into a repeating pattern within a finite number of digits. The repeating part is 142857. This characteristic is typical of fractions where the denominator (when simplified) contains prime factors other than 2 and 5.
The non-terminating nature of the decimal representation highlights the limitations of using decimals to represent all fractions precisely. Fractions offer a more concise and exact representation in such cases.
Practical Applications and Real-World Examples
While the specific scenario of dividing 7 by 98 might not appear frequently in everyday life, the underlying principles of division and decimal representation are used extensively. Consider these examples:
-
Calculating unit prices: If 98 items cost 7 dollars, the price per item is 7 ÷ 98 = $0.0714 (approximately 7 cents per item).
-
Proportion and ratios: Understanding division helps in solving problems involving proportions and ratios. For example, if a recipe calls for 98 grams of flour and you only have 7 grams, you can calculate the fraction of the recipe you can make.
-
Percentage calculations: Dividing 7 by 98 helps calculate percentages. 7/98 represents 7% of 98.
Frequently Asked Questions (FAQ)
-
Q: Why is the decimal representation of 7/98 non-terminating?
- A: A decimal representation terminates only if the fraction, when simplified, has a denominator that is a power of 10 (i.e., only factors of 2 and 5). The simplified fraction 1/14 has a factor of 7 in the denominator, leading to a non-terminating decimal.
-
Q: Is there a way to get the exact decimal value of 7/98?
- A: No, there isn't an exact decimal value because the decimal representation is non-terminating. We can only approximate it to a certain number of decimal places.
-
Q: Which representation is better, fraction or decimal?
- A: For exactness, the fraction (1/14) is superior. Decimals are useful for approximations and for comparisons in certain contexts.
-
Q: Can I use a calculator to find the answer?
- A: Yes, a calculator provides a quick decimal approximation, but it's important to understand the underlying mathematical concepts and the limitations of decimal representation.
Conclusion
Dividing 7 by 98, while seemingly simple, provides a valuable opportunity to reinforce fundamental mathematical concepts. We've explored long division, the conversion to fractions, the significance of non-terminating decimals, and the practical applications of these calculations. Understanding these concepts enhances our mathematical literacy and empowers us to solve a wide range of problems, both in academic settings and in everyday life. Remember that while a calculator provides a quick answer, comprehending the process enhances your mathematical understanding and problem-solving skills significantly. The seemingly simple 7 ÷ 98 opens doors to a deeper appreciation of the intricacies of arithmetic.
Latest Posts
Latest Posts
-
49 Celsius To Fahrenheit
Sep 14, 2025
-
Price For Cream Cheese
Sep 14, 2025
-
2 8 Pounds To Kg
Sep 14, 2025
-
Joke About Nacho Cheese
Sep 14, 2025
-
80 Mph To Kmh
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 7 Divided By 98 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.