7 Percent Of 800
renascent
Sep 21, 2025 · 6 min read
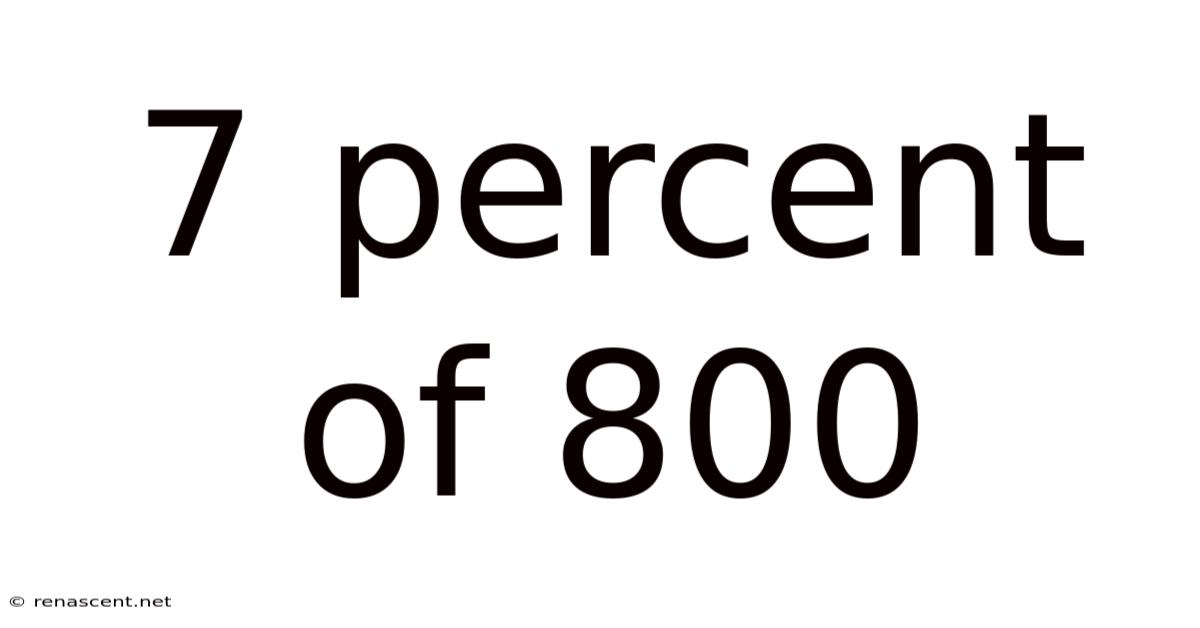
Table of Contents
Unraveling the Mystery: Calculating 7% of 800 and Mastering Percentage Calculations
Finding 7% of 800 might seem like a simple arithmetic problem, but understanding the underlying principles of percentage calculations opens doors to a world of practical applications in various fields, from finance and budgeting to data analysis and scientific research. This comprehensive guide will not only show you how to calculate 7% of 800 using different methods but also equip you with the knowledge and skills to tackle any percentage problem with confidence. We'll explore various approaches, discuss the underlying mathematical concepts, and delve into real-world scenarios where such calculations are vital.
Understanding Percentages: A Foundation for Success
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 7% means 7 out of 100, or 7/100. This fundamental understanding is key to tackling percentage problems efficiently.
Method 1: The Direct Calculation Method
This is the most straightforward method. We convert the percentage to a decimal and multiply it by the given number.
-
Step 1: Convert the percentage to a decimal: To convert 7% to a decimal, we divide it by 100: 7% / 100 = 0.07
-
Step 2: Multiply the decimal by the number: Now, we multiply the decimal (0.07) by 800: 0.07 * 800 = 56
Therefore, 7% of 800 is 56.
This method is efficient and easily adaptable to various percentage calculations. It's the preferred method for most everyday percentage problems.
Method 2: The Fraction Method
This method utilizes the fractional representation of percentages.
-
Step 1: Express the percentage as a fraction: 7% can be written as 7/100.
-
Step 2: Multiply the fraction by the number: We multiply the fraction (7/100) by 800: (7/100) * 800
-
Step 3: Simplify the calculation: We can simplify this by canceling out common factors. 100 goes into 800 eight times: (7/100) * 800 = 7 * 8 = 56
Again, we arrive at the answer: 7% of 800 is 56. This method enhances understanding of the underlying mathematical principles.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We set up a proportion where x represents the unknown value (7% of 800).
-
Step 1: Set up the proportion: We can express the problem as a proportion: 7/100 = x/800
-
Step 2: Cross-multiply: Cross-multiplying gives us: 100x = 7 * 800 = 5600
-
Step 3: Solve for x: Dividing both sides by 100, we get: x = 5600/100 = 56
Therefore, 7% of 800 is 56. This method is particularly useful when dealing with more complex percentage problems or when understanding the proportional relationship is crucial.
Beyond the Basics: Applying Percentage Calculations
Understanding how to calculate 7% of 800 is just the beginning. The ability to perform percentage calculations is crucial in many real-world situations. Let's explore a few examples:
-
Financial Calculations: Calculating interest on loans or savings accounts, determining discounts on purchases, understanding tax rates, and analyzing investment returns all rely heavily on percentage calculations. For instance, if a bank offers a 7% annual interest rate on a savings account with a balance of $800, you would earn $56 in interest after one year.
-
Data Analysis: Percentages are essential for interpreting data in various fields. For example, if 7% of 800 survey respondents answered "yes" to a particular question, this represents 56 respondents. This information is crucial for drawing conclusions and making informed decisions based on the survey data.
-
Scientific Research: In scientific research, percentages are used extensively to express experimental results, error margins, and statistical significance. For example, if a researcher finds that 7% of 800 lab mice exhibited a specific reaction to a treatment, this data point is significant in evaluating the effectiveness of the treatment.
-
Everyday Life: We encounter percentages daily, from calculating tips in restaurants (e.g., a 15% tip on an $80 bill) to understanding sale discounts (e.g., a 20% discount on a $100 item). Mastering percentage calculations makes these everyday tasks easier and more efficient.
Advanced Percentage Calculations: Finding the Percentage and the Whole
While calculating 7% of 800 is a direct application, percentage problems can take various forms. Let's consider two variations:
1. Finding the Percentage: If we know that 56 is a certain percentage of 800, how do we find that percentage?
We set up a proportion: x/100 = 56/800. Cross-multiplying and solving for x yields: x = (56 * 100) / 800 = 7. Therefore, 56 is 7% of 800.
2. Finding the Whole: If 56 represents 7% of a certain number, what is that number?
We again set up a proportion: 7/100 = 56/x. Cross-multiplying and solving for x gives: x = (56 * 100) / 7 = 800. Therefore, 56 is 7% of 800.
These variations highlight the versatility of percentage calculations and the importance of understanding proportional reasoning.
Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes to avoid when calculating percentages?
- A: Common errors include incorrect decimal placement when converting percentages to decimals, improper use of the multiplication or division operations, and failing to properly set up proportions. Careful attention to detail and a methodical approach will minimize these errors.
-
Q: Are there any online tools or calculators for calculating percentages?
- A: Yes, numerous online percentage calculators are available. However, understanding the underlying principles and the ability to perform manual calculations are crucial for developing a deeper understanding of the concept.
-
Q: How can I improve my skills in percentage calculations?
- A: Consistent practice is key. Start with simple problems and gradually progress to more complex ones. Understanding the different methods (direct calculation, fraction method, and proportions) enhances problem-solving flexibility.
-
Q: What if the percentage involves decimals (e.g., 7.5% of 800)?
- A: The same methods apply. Convert the percentage to a decimal (7.5% = 0.075) and multiply by the number (0.075 * 800 = 60).
-
Q: Are there any shortcuts for mental calculation of percentages?
- A: Yes, certain percentages have easy mental shortcuts. For example, 10% is simply dividing by 10, 5% is half of 10%, and 1% is dividing by 100. These shortcuts can be combined to calculate other percentages more efficiently.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 7% of 800, seemingly a simple task, unveils the power and versatility of percentage calculations. This fundamental skill transcends simple arithmetic, providing a critical tool for navigating the complexities of finance, data analysis, and numerous other fields. By understanding the various methods, practicing consistently, and recognizing the real-world applications, you can confidently tackle any percentage problem and unlock a deeper understanding of the world around you. Remember, mastering percentages isn't just about numbers; it's about empowering yourself with a valuable skillset that enhances your problem-solving abilities and contributes to your success in various aspects of life.
Latest Posts
Latest Posts
-
Self Ionisation Of Water
Sep 21, 2025
-
300 Fathoms In Feet
Sep 21, 2025
-
3 Divided By 6
Sep 21, 2025
-
315 Divided By 90
Sep 21, 2025
-
Florida Di License Requirements
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 Percent Of 800 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.