75 Percent Of 20
renascent
Sep 22, 2025 · 5 min read
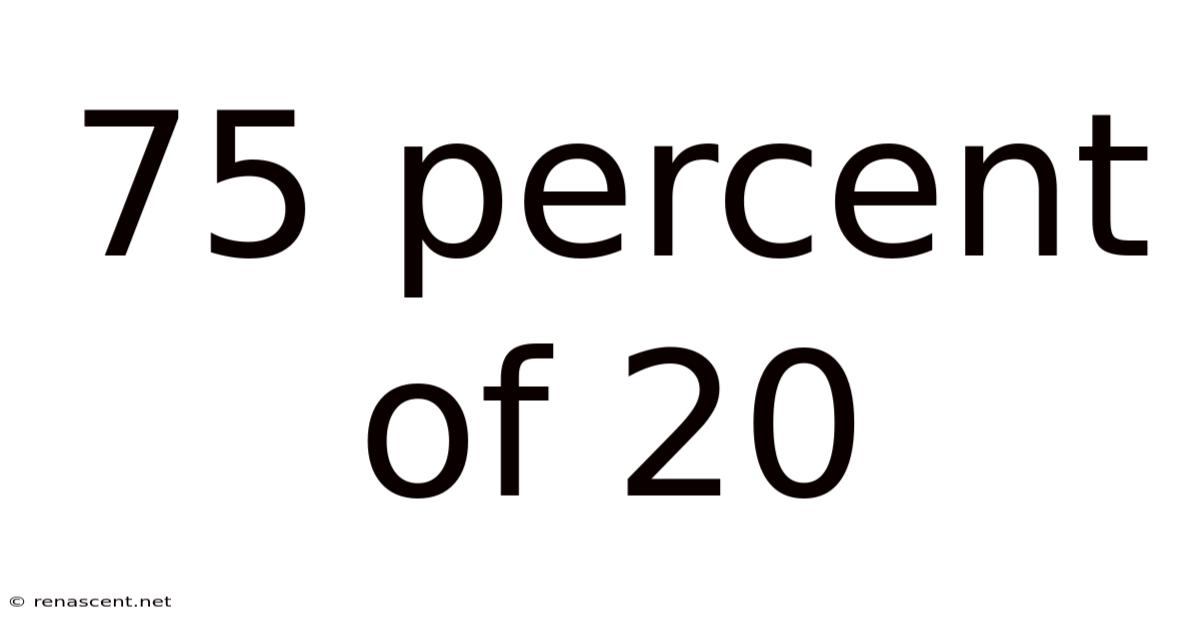
Table of Contents
Decoding 75 Percent of 20: A Comprehensive Guide
Finding 75% of 20 might seem like a simple calculation, easily solvable with a calculator. However, understanding the underlying principles behind percentage calculations is crucial for various applications, from everyday budgeting to advanced financial modeling. This comprehensive guide will not only show you how to calculate 75% of 20 but also delve into the broader concept of percentages, offering multiple approaches to solve this problem and similar ones, enhancing your mathematical proficiency.
Understanding Percentages: The Foundation
A percentage is a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred" ( per cent). Therefore, 75% means 75 out of 100, which can be written as the fraction 75/100 or the decimal 0.75. Understanding this fundamental concept is key to tackling percentage calculations effectively.
Method 1: The Fraction Method
This method uses the fractional equivalent of 75%. As mentioned earlier, 75% is equivalent to 75/100. To find 75% of 20, we simply multiply 20 by the fraction 75/100:
20 * (75/100) = (20 * 75) / 100 = 1500 / 100 = 15
Therefore, 75% of 20 is 15. This method is straightforward and easily understood, especially for those comfortable working with fractions. It’s a great foundational approach.
Method 2: The Decimal Method
This method utilizes the decimal equivalent of 75%, which is 0.75. To find 75% of 20, we multiply 20 by 0.75:
20 * 0.75 = 15
Again, the answer is 15. The decimal method is often preferred for its ease of use with calculators and its efficiency in more complex calculations. This method is particularly useful when dealing with larger numbers or more intricate percentage problems.
Method 3: The Proportion Method
This method leverages the concept of proportion. We can set up a proportion to solve for the unknown value (x), representing 75% of 20:
75/100 = x/20
To solve for x, we cross-multiply:
75 * 20 = 100 * x
1500 = 100x
x = 1500 / 100 = 15
Once more, the answer is 15. The proportion method is a versatile technique that can be applied to a wide range of percentage problems, making it a valuable tool in your mathematical arsenal. It's especially useful when you need to find the percentage of a larger number or when dealing with more complex proportional relationships.
Method 4: Using Percentage Shortcuts
For simple percentages like 75%, we can utilize shortcuts to speed up the calculation. 75% is 3/4 (75/100 simplifies to 3/4). Therefore, we can find 75% of 20 by finding 3/4 of 20:
20 / 4 = 5 (This finds one-quarter of 20)
5 * 3 = 15 (This multiplies the quarter by three to get three-quarters)
The result remains 15. This method highlights the interconnectedness of fractions, decimals, and percentages, offering a more intuitive approach for those comfortable with fraction manipulation. This method is particularly helpful for common percentages such as 25%, 50%, and 75%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical exercises. Here are a few examples of how this skill is applied in everyday life:
-
Sales and Discounts: Calculating discounts on sale items. If a shirt is 20% off and costs $50, you would calculate 20% of $50 (0.20 * $50 = $10) and subtract that amount from the original price.
-
Taxes: Determining the amount of tax to be paid on purchases. Sales tax percentages vary by location.
-
Tips and Gratuities: Calculating the appropriate tip amount at restaurants. A common tip is 15% or 20% of the bill.
-
Financial Calculations: Calculating interest on loans or investments. Understanding compound interest involves repeated percentage calculations.
-
Data Analysis: Representing data visually using pie charts and bar graphs, which rely heavily on percentages. For instance, a survey might show 75% of respondents preferred a particular product.
-
Grading Systems: Many academic institutions use percentages to represent grades. A score of 85% indicates a high level of performance.
Expanding Your Understanding: Calculating Other Percentages
The methods outlined above can be easily adapted to calculate other percentages. For example, let's consider calculating 30% of 50:
Fraction Method: 50 * (30/100) = 15
Decimal Method: 50 * 0.30 = 15
Proportion Method: 30/100 = x/50 => x = 15
These methods demonstrate the versatility and applicability of percentage calculations across a range of scenarios.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage that's not a whole number, such as 12.5% of 20?
A: You can use the same methods, but you'll be working with a decimal value of 0.125 instead of 0.75. For instance: 20 * 0.125 = 2.5
Q: How can I calculate what percentage one number is of another?
A: To find what percentage, say, 15 is of 20, you divide 15 by 20 and multiply by 100: (15/20) * 100 = 75%.
Q: Are there online calculators or tools that can help with percentage calculations?
A: Yes, many online calculators are available that can perform percentage calculations for you. However, understanding the underlying principles remains crucial for problem-solving and a deeper mathematical understanding.
Q: How can I improve my proficiency in percentage calculations?
A: Practice is key! Start with simpler problems and gradually move to more complex ones. Utilize different methods to solve the same problems to build a strong intuitive understanding.
Conclusion: Mastering Percentage Calculations
This comprehensive guide has explored various methods for calculating 75% of 20, emphasizing the importance of understanding the fundamental principles of percentages. From the straightforward fraction method to the more versatile proportion method, each approach provides a pathway to understanding and solving percentage problems. Remember that mastering percentage calculations isn't just about getting the right answer; it's about developing a strong foundation in mathematical concepts that are essential for various aspects of life, from personal finance to academic pursuits and professional endeavors. By practicing regularly and employing the techniques described above, you can significantly improve your proficiency in this crucial area of mathematics. Continue exploring different methods and applications to enhance your understanding further. The more you practice, the more intuitive and efficient these calculations will become.
Latest Posts
Latest Posts
-
1189 Divided By 2
Sep 22, 2025
-
1 3 Of 23
Sep 22, 2025
-
600 Cal To Kj
Sep 22, 2025
-
5 7 As A Percentage
Sep 22, 2025
-
53 Cm In Inch
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 75 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.