806 Divided By 4
renascent
Sep 20, 2025 · 6 min read
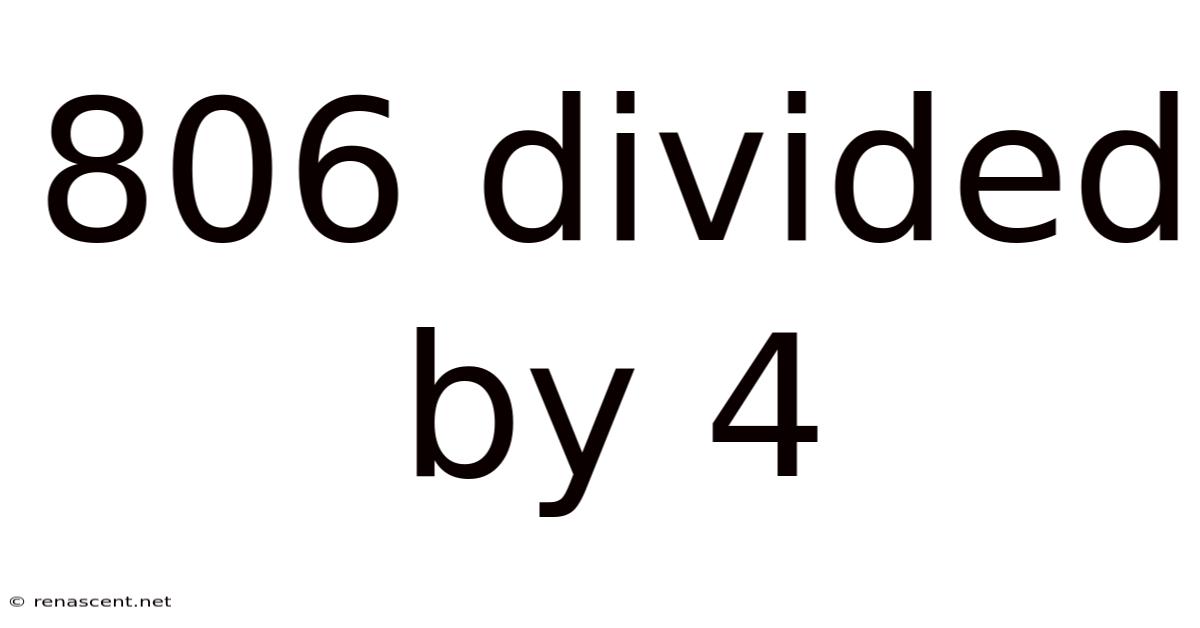
Table of Contents
Unveiling the Magic: A Deep Dive into 806 Divided by 4
Meta Description: Learn how to divide 806 by 4 in multiple ways, from basic long division to insightful explanations perfect for students and anyone curious about the intricacies of division. Master this fundamental arithmetic skill and understand the underlying mathematical principles.
Understanding division is a cornerstone of mathematical literacy. It's a skill that extends far beyond the classroom, impacting everyday life from splitting bills to calculating recipe proportions. This comprehensive guide will delve into the process of dividing 806 by 4, exploring various methods and illuminating the mathematical concepts involved. We'll move beyond a simple answer, uncovering the "why" behind the calculations and solidifying your understanding of division.
I. The Straightforward Approach: Long Division
The most common method for solving 806 divided by 4 is through long division. This method, while seemingly simple, underpins a profound understanding of place value and the distributive property. Let's break down the process step-by-step:
-
Set up the problem: Write the dividend (806) inside the long division symbol (⟌) and the divisor (4) outside.
4 ⟌ 806 -
Divide the hundreds: How many times does 4 go into 8 (the hundreds place)? The answer is 2. Write the 2 above the 8 in the quotient.
2 4 ⟌ 806 -
Multiply and subtract: Multiply the quotient digit (2) by the divisor (4), resulting in 8. Subtract this from the hundreds place of the dividend (8 - 8 = 0).
2 4 ⟌ 806 -8 --- 0 -
Bring down the tens: Bring down the next digit of the dividend (0) next to the remainder (0). This forms the number 0.
2 4 ⟌ 806 -8 --- 00 -
Divide the tens: How many times does 4 go into 0? The answer is 0. Write 0 above the 0 in the quotient.
20 4 ⟌ 806 -8 --- 00 -
Multiply and subtract: Multiply the quotient digit (0) by the divisor (4), resulting in 0. Subtract this from the tens place (0 - 0 = 0).
20 4 ⟌ 806 -8 --- 00 -0 --- 0 -
Bring down the ones: Bring down the next digit of the dividend (6) next to the remainder (0). This forms the number 6.
20 4 ⟌ 806 -8 --- 00 -0 --- 06 -
Divide the ones: How many times does 4 go into 6? The answer is 1 with a remainder of 2. Write the 1 above the 6 in the quotient.
201 4 ⟌ 806 -8 --- 00 -0 --- 06 -4 --- 2
Therefore, 806 divided by 4 is 201 with a remainder of 2. This can also be expressed as 201 R 2 or 201.5.
II. Understanding the Remainder
The remainder of 2 signifies that after dividing 806 into groups of 4, there are 2 elements left over. This remainder is crucial in various applications. For instance, if you're dividing 806 candies equally among 4 friends, each friend gets 201 candies, and you have 2 candies left. Understanding remainders allows for accurate and complete problem-solving.
III. Alternative Methods: Breaking Down the Problem
Instead of relying solely on long division, let's explore a more intuitive approach: breaking down the dividend into manageable parts. This method can be particularly helpful for visualizing the division process.
We can break down 806 as follows: 800 + 6.
-
Dividing 800 by 4: This is relatively straightforward. We know that 8 divided by 4 is 2, so 800 divided by 4 is 200.
-
Dividing 6 by 4: This results in 1 with a remainder of 2.
Adding the results together: 200 + 1 = 201, with a remainder of 2. This confirms the result we obtained through long division.
IV. Decimal Representation
The remainder can also be expressed as a decimal. Since the remainder is 2 and the divisor is 4, we can represent the remainder as a fraction: 2/4. Simplifying this fraction to its lowest terms yields 1/2, which is equivalent to 0.5. Therefore, 806 divided by 4 can also be expressed as 201.5. This decimal representation is useful in contexts where fractional results are acceptable or necessary.
V. The Mathematical Principles at Play
The process of dividing 806 by 4 fundamentally relies on several core mathematical concepts:
-
Place Value: Understanding the value of each digit based on its position (ones, tens, hundreds) is crucial for accurately performing long division.
-
Distributive Property: This property states that a(b + c) = ab + ac. In our case, we essentially distribute the division across the different place values of the dividend.
-
Repeated Subtraction: Division can be viewed as repeated subtraction. We are repeatedly subtracting 4 from 806 until we reach 0 or a number less than 4. The number of times we subtract 4 represents the quotient.
-
Euclidean Division: This fundamental theorem states that for any integers a and b (where b is not zero), there exist unique integers q and r such that a = bq + r, and 0 ≤ r < |b|. Here, a is the dividend (806), b is the divisor (4), q is the quotient (201), and r is the remainder (2).
VI. Real-World Applications
The seemingly simple task of dividing 806 by 4 has broad applications across various fields:
-
Equal Sharing: Distributing resources evenly (candies, money, tasks) among a group.
-
Scaling Recipes: Adjusting ingredient quantities in cooking or baking.
-
Averaging Data: Calculating the average of a set of numerical values.
-
Unit Conversion: Converting between different units of measurement (e.g., meters to centimeters).
-
Rate and Ratio Problems: Solving problems involving rates (speed, price) and ratios (proportions).
VII. Frequently Asked Questions (FAQ)
Q1: Why is the remainder important?
A1: The remainder indicates the portion of the dividend that doesn't divide evenly by the divisor. It provides complete information about the division process and is essential for accurate results in many real-world scenarios.
Q2: Can I use a calculator to solve this problem?
A2: Absolutely! Calculators provide a quick and convenient way to perform division. However, understanding the underlying principles is crucial for developing strong mathematical reasoning skills.
Q3: What if the divisor was a larger number?
A3: The process of long division remains the same, although it might involve more steps. The principles of place value, distributive property, and repeated subtraction still apply.
Q4: How can I improve my division skills?
A4: Practice is key! Work through various division problems, starting with simpler ones and gradually increasing the difficulty. Focus on understanding the underlying principles rather than just memorizing procedures. Utilize online resources, workbooks, and seek help from teachers or tutors if needed.
VIII. Conclusion
Dividing 806 by 4, while a seemingly elementary task, offers a rich opportunity to explore and solidify our understanding of fundamental mathematical concepts. Through various approaches—long division, breaking down the problem, and exploring the remainder—we've gained a deeper appreciation of the intricacies of division. Mastering this skill is not merely about obtaining the correct answer (201 with a remainder of 2 or 201.5); it's about grasping the underlying mathematical principles that empower us to solve a wide range of problems in various contexts. Remember, the journey of learning mathematics is about understanding the "why" as much as the "how." Continue to explore, question, and practice, and you will steadily build your mathematical proficiency and confidence.
Latest Posts
Latest Posts
-
Object Has No Attribute
Sep 20, 2025
-
Yard Convert To Cm
Sep 20, 2025
-
196 Pounds In Kilos
Sep 20, 2025
-
20 Off Of 85
Sep 20, 2025
-
2 73 Kg To Lbs
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 806 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.