85 Divided By 2
renascent
Sep 24, 2025 · 5 min read
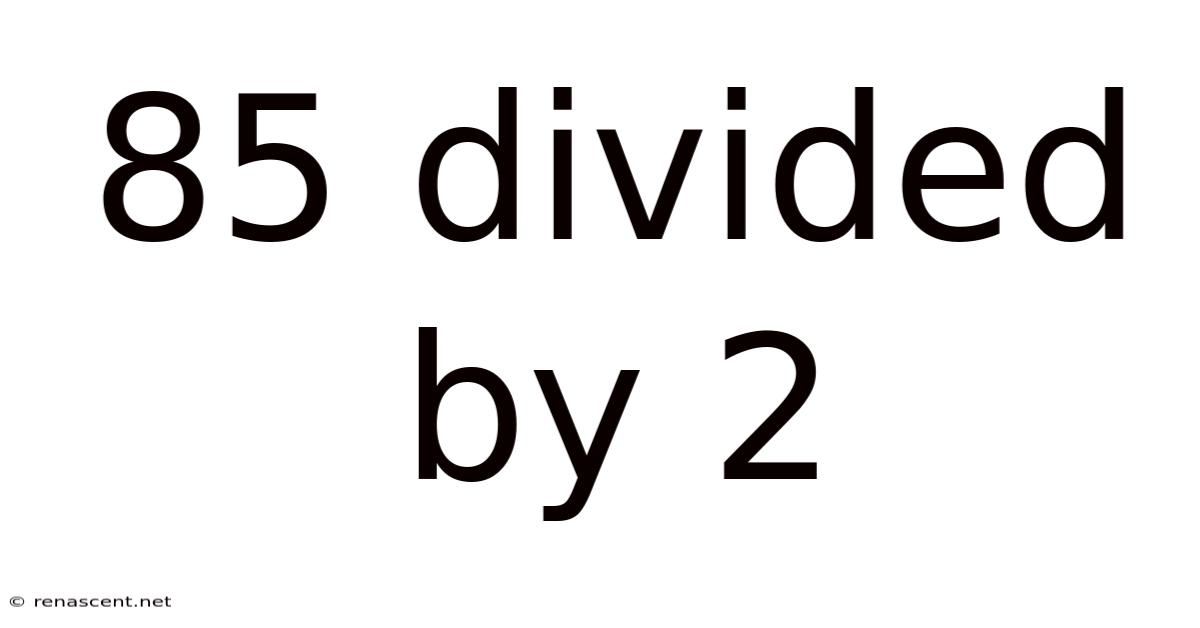
Table of Contents
Decoding 85 Divided by 2: A Deep Dive into Division and its Applications
Introduction: This article explores the seemingly simple problem of 85 divided by 2, delving beyond the immediate answer to uncover the underlying principles of division, its various methods, and its practical applications in everyday life and advanced mathematics. Understanding this seemingly basic operation lays the foundation for more complex mathematical concepts. We'll cover different approaches to solving the problem, including long division, and discuss the significance of remainders and their interpretation. We’ll also touch upon real-world scenarios where division, and specifically this example, might appear.
Understanding Division:
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 85 divided by 2, we are looking to determine how many times 2 goes into 85, and what remains if any. The number being divided (85) is called the dividend, the number we are dividing by (2) is the divisor, the result is the quotient, and any remaining amount is the remainder.
Method 1: Long Division
The traditional method for solving 85 divided by 2 is long division. Here's a step-by-step breakdown:
-
Set up the problem: Write the dividend (85) inside the long division symbol ( ⟌ ) and the divisor (2) outside.
2 ⟌ 85 -
Divide the tens digit: How many times does 2 go into 8 (the tens digit of 85)? It goes in 4 times (4 x 2 = 8). Write the 4 above the 8 in the dividend.
4 2 ⟌ 85 -
Multiply and subtract: Multiply the quotient digit (4) by the divisor (2) (4 x 2 = 8). Subtract this result from the tens digit of the dividend (8 - 8 = 0).
4 2 ⟌ 85 -8 -- 0 -
Bring down the units digit: Bring down the units digit of the dividend (5) next to the 0.
4 2 ⟌ 85 -8 -- 05 -
Divide the units digit: How many times does 2 go into 5? It goes in 2 times (2 x 2 = 4). Write the 2 above the 5 in the dividend.
42 2 ⟌ 85 -8 -- 05 -
Multiply and subtract: Multiply the quotient digit (2) by the divisor (2) (2 x 2 = 4). Subtract this result from the remaining number (5 - 4 = 1).
42 2 ⟌ 85 -8 -- 05 -4 -- 1 -
Remainder: The remaining 1 is the remainder.
Therefore, 85 divided by 2 is 42 with a remainder of 1. We can express this as 42 R1 or 42 1/2.
Method 2: Repeated Subtraction
Another way to approach this problem is through repeated subtraction. We continuously subtract the divisor (2) from the dividend (85) until we reach a number less than the divisor. The number of times we subtract represents the quotient, and the remaining number is the remainder.
85 - 2 = 83 83 - 2 = 81 ...and so on. This method is less efficient for larger numbers but demonstrates the core concept of division. You would continue this process until you arrive at a number less than 2. This method will also yield a quotient of 42 and a remainder of 1.
Method 3: Fractions and Decimals
Instead of expressing the answer with a remainder, we can represent the result as a fraction or a decimal. The remainder (1) becomes the numerator of the fraction, and the divisor (2) becomes the denominator. Thus, 85 divided by 2 can also be expressed as 42 1/2. This fraction can be easily converted to a decimal by dividing the numerator by the denominator (1 ÷ 2 = 0.5), giving us 42.5.
The Significance of the Remainder:
The remainder (1) in this calculation is crucial. It signifies that 85 cannot be perfectly divided into two equal groups. There will always be one unit left over. This concept is essential in various applications, such as:
- Sharing: If you have 85 candies to share equally among 2 friends, each friend gets 42 candies, and you have 1 candy left over.
- Measurement: If you need to cut an 85cm long rope into 2 equal pieces, each piece will be 42.5 cm long.
- Programming: In computer programming, remainders are often used in algorithms and control structures. The modulo operator (%) returns the remainder of a division.
Real-World Applications:
The concept of division, particularly with remainders, finds widespread application across various fields:
- Engineering: Calculating material requirements, dividing workload amongst teams, and ensuring even distribution.
- Finance: Calculating equal payments, splitting costs, or calculating profit margins.
- Science: Analyzing data, performing experiments involving equal groups, and determining averages.
- Everyday Life: Sharing resources, calculating quantities for recipes, or determining the number of trips needed to transport items.
Beyond the Basics: Exploring Further
The seemingly simple problem of 85 divided by 2 opens doors to understanding more advanced mathematical concepts:
- Modular Arithmetic: The remainder plays a key role in modular arithmetic, used extensively in cryptography and computer science.
- Algebra: Division forms the basis for solving algebraic equations and working with fractions and ratios.
- Calculus: Differential calculus uses concepts of infinitesimally small divisions to calculate rates of change.
Frequently Asked Questions (FAQ):
-
Q: Why is the remainder important? A: The remainder indicates that the division is not exact, implying there's an incomplete portion left after splitting the dividend into equal parts. Its interpretation varies depending on the context of the problem.
-
Q: Can I use a calculator to solve this? A: Yes, calculators can quickly perform this division. However, understanding the underlying process through long division or repeated subtraction is essential for grasping the fundamental concepts.
-
Q: What if I had to divide 85 by a larger number? A: The same principles of long division apply, although the process may involve more steps.
-
Q: What if the divisor is zero? A: Division by zero is undefined in mathematics. It's an invalid operation.
Conclusion:
The seemingly straightforward task of dividing 85 by 2 provides a foundation for a much deeper exploration of the principles of division, its various methods, and its extensive applications in diverse fields. While the answer might appear simple (42 with a remainder of 1, or 42.5), the process unveils the essential logic behind division and highlights its importance in mathematics and real-world problem-solving. Understanding this foundational concept opens doors to comprehending more complex mathematical ideas and real-world applications, making it a cornerstone of mathematical literacy.
Latest Posts
Latest Posts
-
Types Of Badminton Hits
Sep 24, 2025
-
3 7 As A Decimal
Sep 24, 2025
-
Collective Name For Rhinos
Sep 24, 2025
-
125 Grams To Ounces
Sep 24, 2025
-
Filipino Festival Melbourne 2024
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 85 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.