9/20 As A Percent
renascent
Sep 19, 2025 · 5 min read
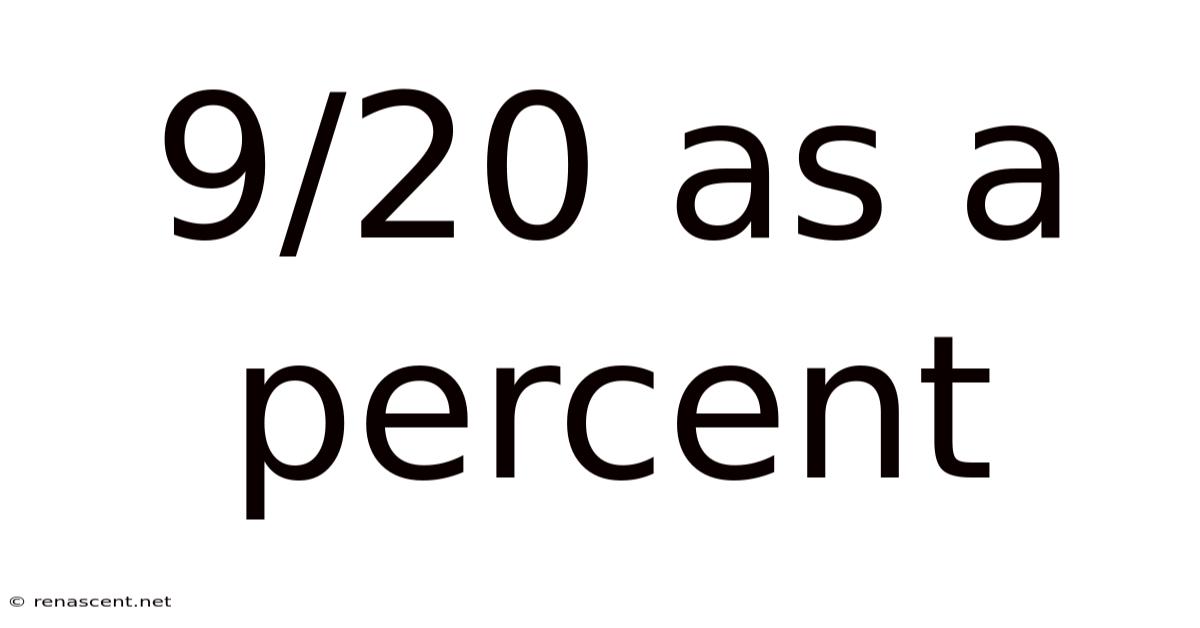
Table of Contents
Decoding 9/20 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistical data and financial reports. This article provides a comprehensive guide to converting the fraction 9/20 into a percentage, exploring different methods and delving into the underlying mathematical principles. We'll cover various approaches, ensuring you grasp not just the answer but also the why behind the calculations. This will empower you to confidently tackle similar fraction-to-percentage conversions in the future.
Understanding Fractions and Percentages
Before diving into the conversion of 9/20, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts in the whole.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Direct Conversion Using Division
The most straightforward method to convert a fraction to a percentage is through division. We divide the numerator by the denominator and then multiply the result by 100.
Steps:
- Divide the numerator by the denominator: 9 ÷ 20 = 0.45
- Multiply the result by 100: 0.45 × 100 = 45
Therefore, 9/20 is equal to 45%.
This method is based on the fundamental principle that a percentage is a fraction with a denominator of 100. By dividing the numerator by the denominator, we find the decimal equivalent of the fraction. Multiplying by 100 then scales this decimal to represent the proportion out of 100, which is the definition of a percentage.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction with a denominator of 100. This method relies on the principle that multiplying or dividing both the numerator and the denominator of a fraction by the same number does not change the fraction's value.
Steps:
- Determine the factor to multiply the denominator by to get 100: We need to multiply 20 by 5 to get 100 (20 x 5 = 100).
- Multiply both the numerator and the denominator by this factor: (9 x 5) / (20 x 5) = 45/100
- Express the equivalent fraction as a percentage: 45/100 = 45%
This method visually demonstrates the relationship between the fraction and its percentage equivalent. It highlights that 45/100 directly represents 45 out of 100, hence 45%.
Method 3: Using Proportions
Proportions offer a powerful tool for solving various mathematical problems, including fraction-to-percentage conversions. We can set up a proportion to solve for the percentage equivalent.
Steps:
- Set up a proportion: 9/20 = x/100, where 'x' represents the percentage we want to find.
- Cross-multiply: 9 × 100 = 20 × x
- Solve for x: 900 = 20x => x = 900 ÷ 20 = 45
Therefore, x = 45, meaning 9/20 is 45%.
This method demonstrates the equivalence between the two ratios. We're essentially scaling the fraction 9/20 to an equivalent fraction with a denominator of 100, allowing us to directly read the percentage.
Real-World Applications of 9/20 as 45%
The conversion of 9/20 to 45% has practical applications in various real-world scenarios. For example:
- Sales and Discounts: A store offering a 45% discount on an item is essentially offering a reduction equivalent to 9/20 of the original price.
- Surveys and Statistics: If 9 out of 20 people surveyed prefer a particular product, this translates to a 45% preference rate.
- Grades and Assessments: In a test with 20 questions, scoring 9 correct answers represents a 45% score.
- Financial Calculations: Understanding percentages is crucial in calculating interest rates, profits, and losses. A 45% profit margin, for instance, indicates a profit equal to 9/20 of the revenue.
Further Exploration: Working with More Complex Fractions
While we focused on 9/20, the principles discussed apply to converting any fraction to a percentage. For fractions with larger numbers, a calculator might be helpful for the division step, but the underlying methods remain the same. For example, to convert 17/25 to a percentage:
- Divide: 17 ÷ 25 = 0.68
- Multiply by 100: 0.68 × 100 = 68%
Therefore, 17/25 is equal to 68%.
Frequently Asked Questions (FAQs)
Q: Can I convert a percentage back into a fraction?
A: Absolutely! To convert a percentage to a fraction, simply write the percentage as a fraction over 100 and then simplify if possible. For example, 75% is 75/100, which simplifies to 3/4.
Q: What if the division results in a repeating decimal?
A: When dealing with repeating decimals, you can either round the decimal to a certain number of places (e.g., two decimal places for common usage) or express the percentage using a fraction. For example, 1/3 = 0.333... This can be expressed as approximately 33.33% or precisely as 33 1/3%.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare proportions. They are frequently used in various contexts, making it easier to understand data, make comparisons, and make informed decisions across diverse fields.
Q: Are there any online tools to help with fraction-to-percentage conversions?
A: Yes, many online calculators and converters are available to assist with these conversions. However, understanding the underlying mathematical principles is crucial for developing problem-solving skills and avoiding over-reliance on tools.
Conclusion
Converting 9/20 to a percentage, resulting in 45%, is a straightforward process once the underlying principles of fractions and percentages are understood. We explored three different methods: direct division, finding an equivalent fraction with a denominator of 100, and using proportions. Each method reinforces the fundamental concepts and provides a different perspective on the same problem. Mastering these methods empowers you to confidently tackle similar conversions and apply this crucial mathematical skill to various real-world situations. Remember, the key is not just to get the answer but to understand the why behind the calculations, building a strong foundation in mathematical reasoning.
Latest Posts
Latest Posts
-
Convert Kpa To Mmhg
Sep 19, 2025
-
Stakeholder Power Interest Grid
Sep 19, 2025
-
Lewis Dot Structure Sis2
Sep 19, 2025
-
Placing Decimals In Order
Sep 19, 2025
-
128 Lb To Kg
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 9/20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.