9 X 2 X
renascent
Sep 14, 2025 · 6 min read
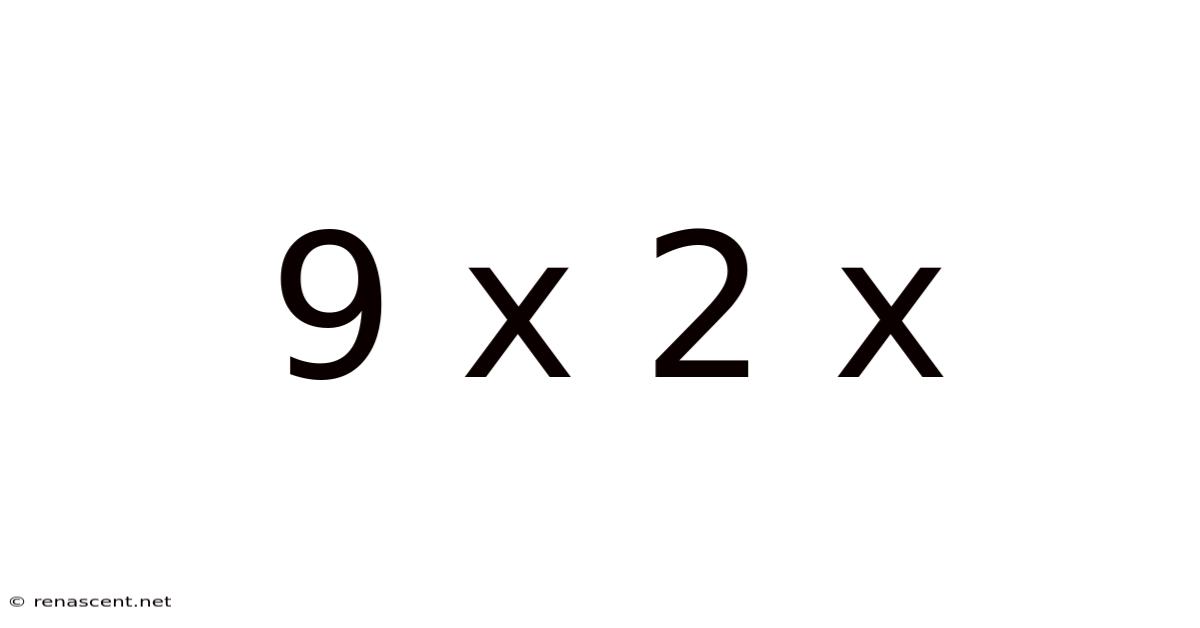
Table of Contents
Unveiling the Mysteries of 9 x 2 x: Beyond the Basic Multiplication
This article delves into the seemingly simple mathematical expression "9 x 2 x," exploring its fundamental meaning, its applications in various fields, and its potential for deeper mathematical exploration. We'll uncover the significance of this calculation, moving beyond the basic answer to understand its implications within broader mathematical contexts. We will also address common misconceptions and frequently asked questions. Understanding 9 x 2 x is not just about getting the right answer; it's about grasping the underlying principles of multiplication and its power in problem-solving.
Understanding the Fundamentals: What Does 9 x 2 x Mean?
At its core, "9 x 2 x" represents a multiplication problem. The "x" symbol signifies the multiplication operation. However, the expression is incomplete; it lacks a third number to complete the multiplication. This incompleteness invites us to explore the concept of variables and the power of open-ended mathematical expressions. We can represent this incomplete expression algebraically as 9 * 2 * x, where 'x' represents an unknown variable. The solution, therefore, depends entirely on the value assigned to 'x'.
- If x = 1: 9 x 2 x 1 = 18
- If x = 2: 9 x 2 x 2 = 36
- If x = 3: 9 x 2 x 3 = 54
- If x = 0: 9 x 2 x 0 = 0
- If x = -1: 9 x 2 x -1 = -18
This simple example highlights the importance of understanding variables and the flexibility of mathematical expressions. The incompleteness isn't a flaw; it’s a feature, allowing for exploration and problem-solving based on different contexts.
Applications Across Disciplines: Where Does 9 x 2 x Appear?
While seemingly basic, the principles behind 9 x 2 x have far-reaching implications across various disciplines. Let's explore some examples:
1. Everyday Calculations: Imagine you're buying nine packs of cookies, each containing two rows of cookies, and each row has 'x' number of cookies. The total number of cookies would be represented by 9 x 2 x x. This demonstrates how simple multiplication can be used to solve real-world problems related to quantity and counting.
2. Geometry and Area Calculation: Consider a rectangle with a length of 9 units and a width of 2 units. If you divide the rectangle into 'x' equal parts, the area of each part would be calculated using the expression: (9 * 2) / x. This highlights the application of multiplication and division in solving geometric problems.
3. Algebra and Equation Solving: In algebra, the expression 9 x 2 x can be part of a larger equation that needs to be solved for 'x'. For example, 9 x 2 x = 72 becomes a simple algebraic equation where solving for 'x' requires dividing both sides by 18 (9 x 2 = 18). This leads to x = 4. This shows how basic multiplication is fundamental to more complex algebraic manipulations.
4. Programming and Computer Science: In programming, the expression 9 x 2 x is a straightforward representation of a multiplication operation that can be used within larger programs or algorithms. The flexibility of assigning a value to 'x' is crucial for creating dynamic and adaptable code.
5. Physics and Engineering: The concept of scaling and proportion often involves multiplication. For instance, if a certain force produces an acceleration of 9 units, and that force is doubled (2), the resulting acceleration might be dependent on another factor ('x'), expressed as 9 x 2 x. The exact relationship would depend on the specific physical laws at play.
Exploring Deeper Mathematical Concepts: Beyond Simple Calculation
The simple expression 9 x 2 x offers an entry point into exploring several crucial mathematical concepts:
1. The Commutative Property: Multiplication is commutative, meaning the order of the numbers doesn't change the result. This means 9 x 2 x x = 2 x 9 x x = x x 9 x 2, and so on. This seemingly trivial property is fundamental to many mathematical operations.
2. The Associative Property: Similarly, the associative property states that the grouping of numbers in multiplication doesn't affect the outcome. (9 x 2) x x = 9 x (2 x x). This property allows for flexibility in calculation strategies.
3. The Distributive Property: When dealing with more complex expressions involving addition or subtraction, the distributive property comes into play. For example, 9 x (2 + x) = (9 x 2) + (9 x x). This property allows us to simplify and manipulate complex expressions.
4. Variables and Functions: The 'x' in the expression acts as a variable, which can take on various values. This introduces the concept of functions where the output (the result of 9 x 2 x) depends on the input (the value of 'x'). This is a fundamental concept in higher-level mathematics and programming.
5. Order of Operations (PEMDAS/BODMAS): While this expression is simple, the order of operations becomes critical when dealing with more complex calculations involving other mathematical operations like addition, subtraction, division, exponents, parentheses, and brackets. Understanding PEMDAS/BODMAS is essential for accurate calculations.
Common Misconceptions and Addressing Them
A common misconception surrounding the expression 9 x 2 x is the assumption that the 'x' automatically represents the variable 'x' as used in Algebra. While this is a valid interpretation in many contexts, it's crucial to understand that the 'x' symbol can also simply be an indicator of an incomplete multiplication problem requiring a third numerical value to be provided. The context of the problem will determine the correct interpretation.
Frequently Asked Questions (FAQ)
Q1: What is the answer to 9 x 2 x?
A1: There is no single answer to 9 x 2 x without knowing the value of 'x'. The expression is incomplete and requires a numerical value to be substituted for 'x' to get a definitive answer.
Q2: Can 'x' be a decimal or fraction?
A2: Yes, absolutely. 'x' can represent any real number, including decimals and fractions. This adds to the flexibility and generality of the expression.
Q3: How is 9 x 2 x used in advanced mathematics?
A3: The principles underlying 9 x 2 x, such as variables, functions, and the properties of multiplication, form the foundation for many advanced mathematical concepts like calculus, linear algebra, and abstract algebra.
Q4: Why is understanding 9 x 2 x important?
A4: Understanding 9 x 2 x isn't just about solving a simple multiplication problem; it’s about grasping fundamental mathematical principles that underpin countless applications across various fields, strengthening your problem-solving skills, and preparing you for more advanced mathematical concepts.
Conclusion: The Power of Simplicity
The expression "9 x 2 x" might appear deceptively simple, but it encapsulates a wealth of mathematical concepts and applications. By exploring its nuances, we've uncovered the importance of understanding variables, the properties of multiplication, and the broader context within which simple mathematical expressions can be applied. From everyday calculations to advanced mathematical theories, the core principles embodied in this seemingly straightforward expression form the backbone of mathematical understanding and problem-solving. Remember, the journey of mathematical understanding is often paved with these small, fundamental concepts, each holding a powerful key to unlocking larger mathematical landscapes. The next time you encounter a simple-looking mathematical expression, take a moment to appreciate its depth and potential.
Latest Posts
Latest Posts
-
172 Lbs To Kg
Sep 14, 2025
-
55 As A Fraction
Sep 14, 2025
-
161 Minutes To Hours
Sep 14, 2025
-
Comedian George Carlin Quotes
Sep 14, 2025
-
Factor 2x 2 X
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 9 X 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.