Square Root Of 130
renascent
Sep 18, 2025 · 6 min read
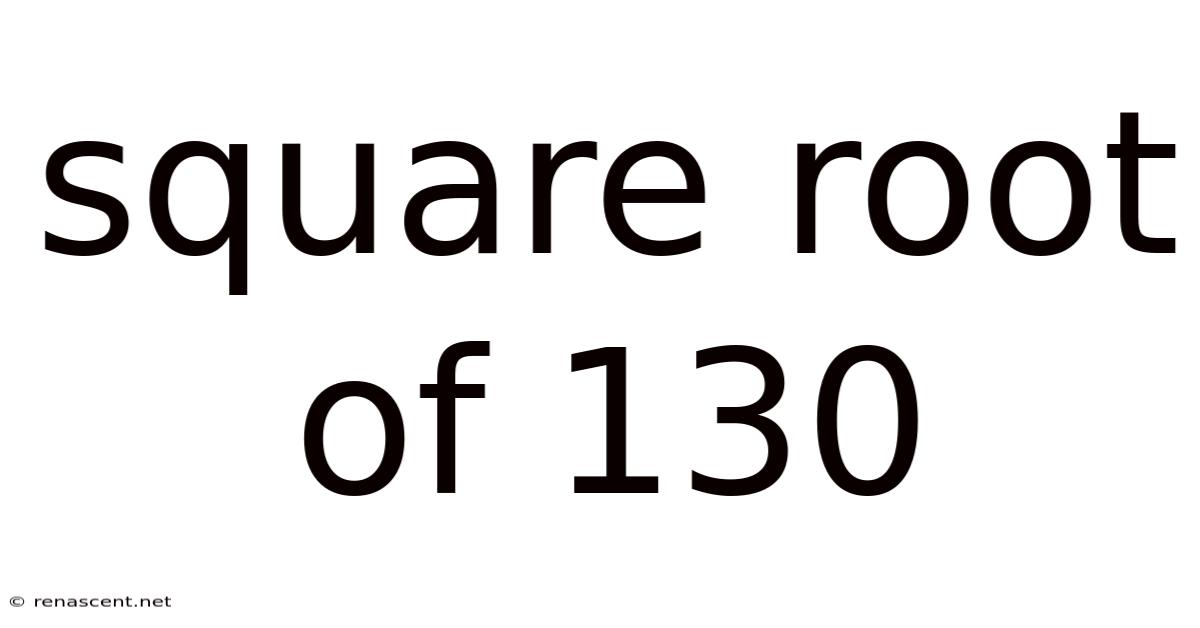
Table of Contents
Unveiling the Mysteries of the Square Root of 130: A Deep Dive into Approximation and Calculation
Finding the square root of 130 might seem like a simple mathematical task, but it delves into fascinating concepts within number theory and numerical analysis. Unlike the perfect squares (numbers whose square roots are whole numbers), 130's square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. This article explores various methods for approximating √130, examining both historical techniques and modern computational approaches, explaining the underlying mathematical principles along the way. We'll also delve into the practical applications of understanding square roots and their significance in different fields.
Understanding Square Roots: A Foundational Overview
Before we tackle the square root of 130 specifically, let's revisit the fundamental concept of a square root. The square root of a number 'x' is a value that, when multiplied by itself, equals 'x'. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. This relationship is expressed mathematically as: √x = y if and only if y² = x.
Perfect squares, as mentioned earlier, are numbers that result from squaring a whole number. Examples include 1, 4, 9, 16, 25, and so on. However, most numbers are not perfect squares, leading to irrational square roots like √130.
Methods for Approximating √130
There are several methods to approximate the square root of 130. Let's explore some of the most common and effective ones:
1. The Babylonian Method (or Heron's Method): An Iterative Approach
This ancient method, dating back to the time of the Babylonians, is an iterative process that refines an initial guess to get increasingly closer to the true value. The formula is:
x_(n+1) = 0.5 * (x_n + (a/x_n))
where:
- x_n is the current approximation
- x_(n+1) is the next, improved approximation
- 'a' is the number whose square root is being calculated (in our case, 130)
Let's demonstrate this with √130. We start with an initial guess, say, x_0 = 11 (since 11² = 121, which is close to 130).
- Iteration 1: x_1 = 0.5 * (11 + (130/11)) ≈ 11.045
- Iteration 2: x_2 = 0.5 * (11.045 + (130/11.045)) ≈ 11.04536
- Iteration 3: x_3 = 0.5 * (11.04536 + (130/11.04536)) ≈ 11.045361
As you can see, the value converges quickly. After just a few iterations, we have a highly accurate approximation of √130. The Babylonian method is remarkably efficient and converges quadratically, meaning the number of correct digits roughly doubles with each iteration.
2. Using a Calculator or Computer Software: The Modern Approach
Modern calculators and computer software provide highly accurate approximations of square roots with a single button press. These tools utilize sophisticated algorithms, often based on variations of the Babylonian method or other advanced numerical techniques, to calculate square roots to many decimal places. For √130, a calculator would provide a result such as 11.40175425...
3. Linear Approximation: A Simpler, Less Precise Method
For a quick, rough estimate, we can use linear approximation. We know that √121 = 11 and √144 = 12. Since 130 lies between 121 and 144, its square root will be between 11 and 12. We can use linear interpolation to estimate:
The difference between 144 and 121 is 23. 130 is 9 units away from 121. Therefore, a rough estimate is 11 + (9/23) ≈ 11.39
This method is less accurate than the Babylonian method or calculator methods, but it provides a reasonable approximation quickly without needing complex calculations.
4. Continued Fractions: An Elegant Mathematical Representation
Continued fractions offer an elegant way to represent irrational numbers. While calculating the continued fraction for √130 is more involved than other methods, it provides an infinite representation that converges to the exact value. The continued fraction representation for √130 is:
11 + 1/(2 + 1/(1 + 1/(1 + 1/(2 + 1/(22+...)))))
This representation offers a unique way to approximate √130 by truncating the continued fraction at a desired point. The more terms we include, the more accurate our approximation becomes.
Understanding Irrational Numbers: The Nature of √130
As highlighted earlier, √130 is an irrational number. This means it cannot be expressed as a fraction of two integers (a/b, where 'a' and 'b' are integers and b ≠ 0). Its decimal representation is non-terminating and non-repeating, stretching infinitely without ever settling into a predictable pattern. This is a fundamental characteristic of many square roots of non-perfect squares. The infinitude of the decimal expansion reflects the inherent complexity within the mathematical structure of irrational numbers.
Practical Applications of Square Roots and √130 (Hypothetical Example)
While √130 might not appear in everyday calculations, understanding square roots is essential in numerous applications across various fields.
Consider a hypothetical scenario: You're designing a square-shaped garden with an area of 130 square meters. To determine the length of each side, you would need to calculate √130. The resulting value would guide you in planning the garden's dimensions and purchasing the necessary materials.
Similarly, square roots are crucial in:
- Physics: Calculating distances, velocities, and energies in various physical problems.
- Engineering: Designing structures, calculating forces, and optimizing designs.
- Computer graphics: Calculating distances and positions in 2D and 3D graphics.
- Finance: Calculating investment returns and risk assessments.
Frequently Asked Questions (FAQ)
Q: Is there an exact value for √130?
A: No, there is no exact decimal representation for √130. It's an irrational number, meaning its decimal expansion continues infinitely without repeating. However, we can approximate it to any desired degree of accuracy using the methods described above.
Q: Why is the Babylonian method so effective?
A: The Babylonian method is effective because it converges quadratically. This means that the number of correct decimal places roughly doubles with each iteration, making it a very efficient method for approximating square roots.
Q: Are there other methods for approximating square roots besides the ones mentioned?
A: Yes, there are many other methods, including Newton-Raphson method, which is a generalization of the Babylonian method, and various numerical analysis techniques designed for faster convergence.
Q: What is the significance of irrational numbers?
A: Irrational numbers are fundamental to mathematics and have significant implications in various fields. They demonstrate the richness and complexity of the number system and play crucial roles in geometry, calculus, and other advanced mathematical concepts.
Conclusion: A Deeper Appreciation of √130
The seemingly simple question of finding the square root of 130 opens a door to a rich understanding of number theory, numerical analysis, and the fascinating world of irrational numbers. Whether we employ the ancient Babylonian method, leverage modern computational tools, or explore the elegant representation of continued fractions, each approach provides valuable insights into the nature of square roots and their significance in both theoretical and practical applications. The pursuit of √130, though seemingly simple, underscores the depth and beauty inherent in mathematics. It is a reminder that even the most fundamental concepts can lead us to explore intricate and rewarding mathematical landscapes.
Latest Posts
Latest Posts
-
103 F En C
Sep 18, 2025
-
57 Inches To Ft
Sep 18, 2025
-
Average Weight Of Potato
Sep 18, 2025
-
Square Root Of 214
Sep 18, 2025
-
30 Cm To Mm
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 130 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.