Square Root Of 250
renascent
Sep 16, 2025 · 6 min read
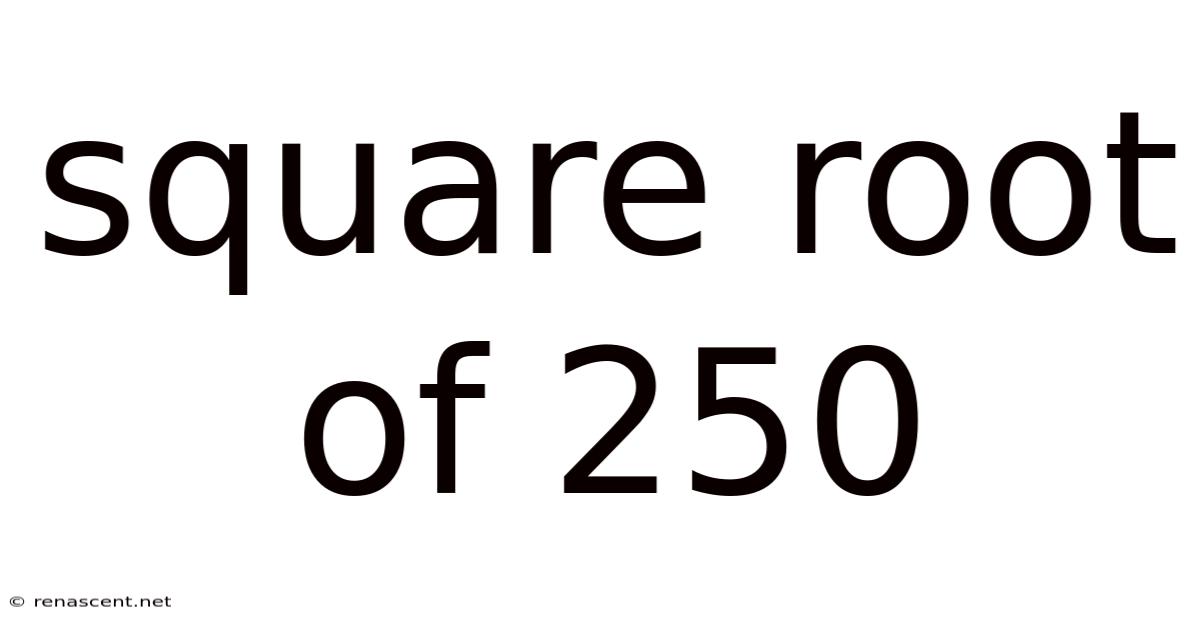
Table of Contents
Unveiling the Mystery: Understanding the Square Root of 250
Finding the square root of 250 might seem like a simple mathematical problem, but it opens a door to a deeper understanding of numbers, their properties, and various methods of calculation. This article will delve into the intricacies of calculating the square root of 250, exploring both the approximate and precise solutions, and explaining the underlying mathematical concepts. We'll also touch upon practical applications and address frequently asked questions. By the end, you'll not only know the answer but also grasp the broader mathematical principles at play.
Understanding Square Roots
Before we tackle the square root of 250, let's refresh our understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. This concept is fundamental in many areas of mathematics and its applications in the real world.
The square root of 250, denoted as √250, is a number that, when multiplied by itself, results in 250. Unlike the square root of 9, which is a whole number, the square root of 250 is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Calculating the Square Root of 250: Methods and Approaches
There are several ways to approach finding the square root of 250. Let's examine some of the most common methods:
1. Prime Factorization and Simplification
The first step towards understanding √250 is to simplify it using prime factorization. Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves).
250 can be factored as follows:
250 = 2 x 125 = 2 x 5 x 25 = 2 x 5 x 5 x 5 = 2 x 5³
Therefore, √250 can be written as √(2 x 5³). We can simplify this by taking out pairs of identical factors from under the square root sign:
√(2 x 5³) = √(2 x 5² x 5) = 5√(2 x 5) = 5√10
This simplifies the square root to 5√10. This is a more concise and often preferred form, representing the exact value.
2. Using a Calculator
The easiest way to find an approximate value for √250 is to use a calculator. Most calculators have a square root function (√). Simply input 250 and press the square root button. The calculator will provide an approximate decimal value, typically around 15.8113883008.
3. Estimation and Iteration Methods
For a deeper understanding and in situations where a calculator isn't available, estimation and iterative methods can be employed. One such method is the Babylonian method (also known as Heron's method), an iterative algorithm that refines an initial guess to progressively closer approximations of the square root.
Here's a simplified explanation of the Babylonian method:
-
Start with an initial guess: Let's guess 16 (because 16 x 16 = 256, which is close to 250).
-
Improve the guess: Divide the number (250) by the guess (16) and then average the result with the guess: (16 + 250/16) / 2 ≈ 15.625
-
Repeat: Use the improved guess (15.625) as the new guess and repeat step 2. (15.625 + 250/15.625) / 2 ≈ 15.8115
-
Continue iterating: Repeating this process multiple times will yield increasingly accurate approximations of the square root of 250.
4. Long Division Method for Square Roots
A more manual, albeit lengthy, method is the long division method for finding square roots. This method involves systematically dividing and subtracting to progressively approximate the square root. It's a more complex process and is less commonly used in today's age of calculators, but it provides a good understanding of the underlying logic.
The Significance of Irrational Numbers: Why √250 is not a Whole Number
As mentioned earlier, √250 is an irrational number. This means its decimal representation is non-terminating and non-repeating. This is a fundamental property of many square roots, particularly those of non-perfect squares (numbers that are not the product of a whole number multiplied by itself). Irrational numbers are an essential part of mathematics and appear extensively in various mathematical fields and real-world applications.
Practical Applications of Square Roots
Square roots, and the related concept of squaring, have numerous applications across various disciplines. Here are a few examples:
-
Geometry: Calculating the diagonal of a square or rectangle (Pythagorean theorem), finding the radius of a circle given its area, and determining the distance between two points using coordinate geometry.
-
Physics: Calculations related to velocity, acceleration, and energy often involve square roots. For example, calculating the speed of a falling object.
-
Engineering: Square roots are integral to structural calculations, determining the strength of materials, and designing various structures.
-
Finance: Calculating investment returns, understanding compound interest, and evaluating financial models frequently utilize square roots.
-
Computer Graphics: Square roots are fundamental in 2D and 3D graphics programming for calculations involving vectors, distances, and transformations.
Frequently Asked Questions (FAQ)
Q: Is there a single, exact value for √250?
A: No, the exact value of √250 is an irrational number, meaning its decimal representation is infinite and non-repeating. While we can express it as 5√10 or obtain close approximations using calculators or iterative methods, there is no single, finite decimal representation.
Q: Why is prime factorization important in simplifying square roots?
A: Prime factorization allows us to identify pairs of factors. We can then "take out" these pairs from under the square root symbol, simplifying the expression. This leads to a more concise and manageable form of the square root.
Q: Which method is best for calculating √250?
A: For quick and accurate results, a calculator is the most practical option. However, understanding prime factorization and the concept of irrational numbers provides a more profound understanding of the underlying mathematics. Iterative methods like the Babylonian method provide insight into numerical approximation techniques.
Q: Can I use a different initial guess in the Babylonian method?
A: Yes, you can use a different initial guess in the Babylonian method. While a closer initial guess will likely lead to faster convergence, the method will eventually converge to the correct answer regardless of the initial guess, provided the guess is a positive number.
Q: Are there any other methods to calculate square roots?
A: Yes, several other methods exist, including numerical methods employed in computer programming, but those tend to be significantly more complex and are beyond the scope of this introductory explanation.
Conclusion
Calculating the square root of 250 provides a practical example to explore the concepts of square roots, irrational numbers, and various calculation methods. While a calculator readily provides an approximate decimal value, understanding the underlying mathematical principles, such as prime factorization and iterative approximation techniques, enriches our understanding of numbers and their properties. The significance of square roots extends far beyond simple mathematical exercises; they play crucial roles in numerous fields, from geometry and physics to finance and computer science. This comprehensive exploration should empower you not only to solve this specific problem but also to tackle similar mathematical challenges with confidence and a deeper understanding.
Latest Posts
Latest Posts
-
6 Lbs 1 Oz
Sep 16, 2025
-
73 5 Kg To Pounds
Sep 16, 2025
-
1 66 M In Feet
Sep 16, 2025
-
Mac Address From Ping
Sep 16, 2025
-
5250 Divided By 2
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.