Square Root Of 324
renascent
Sep 22, 2025 · 6 min read
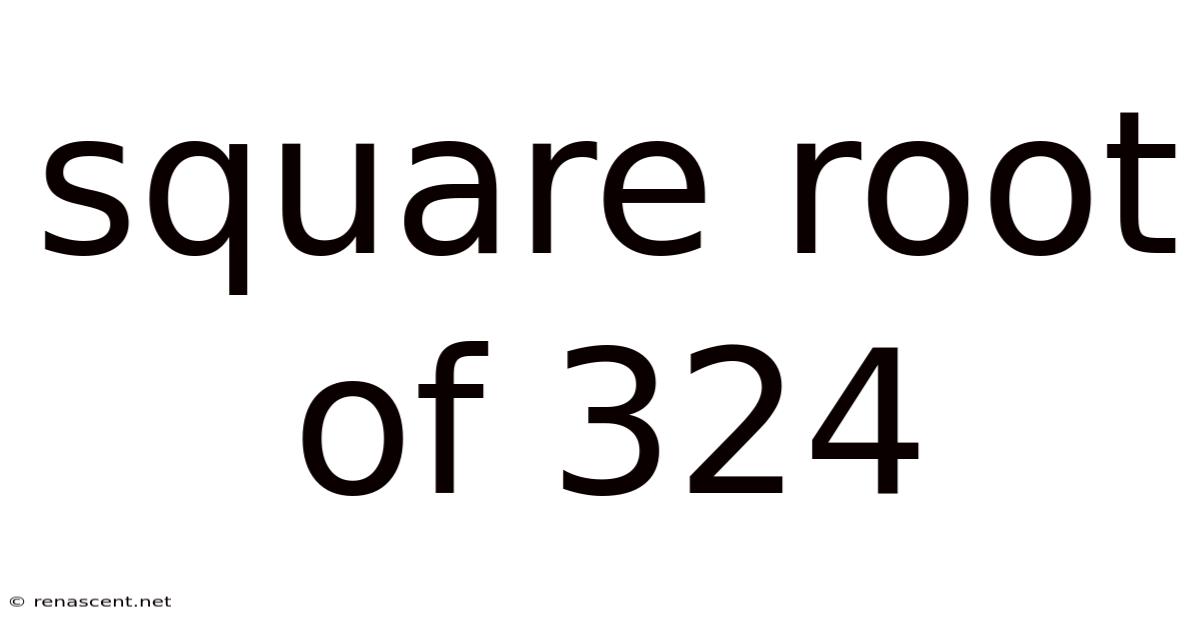
Table of Contents
Unveiling the Mystery: A Deep Dive into the Square Root of 324
Finding the square root of a number might seem like a simple mathematical task, but understanding the underlying principles and exploring different methods of calculation can reveal a surprisingly rich area of mathematical understanding. This article delves into the square root of 324, not just providing the answer, but also exploring the concept of square roots, various methods for calculating them, and their applications in different fields. We'll uncover the beauty of mathematics hidden within this seemingly straightforward problem. Understanding the square root of 324 opens doors to a deeper appreciation of numerical relationships and mathematical processes.
Introduction: What is a Square Root?
Before we dive into the specifics of √324, let's establish a solid understanding of what a square root actually is. Simply put, the square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. This concept is fundamental to many areas of mathematics, science, and engineering. The square root is the inverse operation of squaring a number.
We often encounter the square root symbol, √, which is also known as a radical. The number inside the radical symbol is called the radicand. In our case, the radicand is 324. Finding the square root of 324 means finding a number that, when multiplied by itself, equals 324.
Methods for Calculating the Square Root of 324
There are several ways to calculate the square root of 324. Let's explore a few, ranging from simple estimation to more advanced techniques:
1. Prime Factorization: This method is particularly useful for larger numbers. It involves breaking down the number into its prime factors. Prime factorization is the process of finding the prime numbers that multiply together to make the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
-
Step 1: Find the prime factors of 324. We can do this by repeatedly dividing by prime numbers:
324 ÷ 2 = 162 162 ÷ 2 = 81 81 ÷ 3 = 27 27 ÷ 3 = 9 9 ÷ 3 = 3 3 ÷ 3 = 1
-
Step 2: Express 324 as a product of its prime factors: 2 x 2 x 3 x 3 x 3 x 3 = 2² x 3⁴
-
Step 3: To find the square root, we take half the exponent of each prime factor: √(2² x 3⁴) = 2¹ x 3² = 2 x 9 = 18
Therefore, the square root of 324 is 18.
2. Estimation and Trial and Error: For smaller numbers like 324, estimation can be a quick method. We know that 10² = 100 and 20² = 400, so the square root of 324 must be between 10 and 20. We can then try different numbers within that range until we find one that, when squared, equals 324. 18 x 18 = 324, so the square root is 18.
3. Using a Calculator: The simplest and most efficient way to find the square root of 324 is to use a calculator. Most calculators have a square root function (√), usually denoted by a symbol resembling a checkmark. Simply enter 324 and press the √ button. The calculator will instantly return the answer: 18.
4. Babylonian Method (or Heron's Method): This is an iterative method for approximating square roots, useful for numbers where the square root is not immediately obvious. It refines an initial guess through successive approximations.
-
Step 1: Make an initial guess. Let's guess 15.
-
Step 2: Divide the number (324) by the guess: 324 ÷ 15 ≈ 21.6
-
Step 3: Average the guess and the result from Step 2: (15 + 21.6) / 2 ≈ 18.3
-
Step 4: Repeat steps 2 and 3 using the new average as the guess. 324 ÷ 18.3 ≈ 17.7
-
Step 5: (18.3 + 17.7) / 2 = 18
The method converges quickly towards the correct answer, 18.
The Significance of the Square Root of 324
The square root of 324, being 18, holds significance beyond a simple calculation. It demonstrates fundamental mathematical principles and finds application in various fields:
-
Geometry: In geometry, the square root is crucial for calculating the lengths of sides in right-angled triangles using the Pythagorean theorem (a² + b² = c²). If you know the areas of squares, finding the side lengths involves square roots. For instance, if a square has an area of 324 square units, its side length is √324 = 18 units.
-
Algebra: Square roots are essential in solving quadratic equations (equations of the form ax² + bx + c = 0). The quadratic formula involves the square root to find the solutions for x.
-
Physics: Square roots are frequently used in physics, particularly in calculations involving velocity, acceleration, and energy. Many physical formulas utilize squared terms, and finding the original values often requires taking the square root.
-
Engineering: Engineers use square roots extensively in structural calculations, determining forces and stresses within structures.
Frequently Asked Questions (FAQs)
-
Q: Is there only one square root of 324?
- A: No, technically there are two square roots of 324: 18 and -18. This is because (-18) x (-18) = 324. However, when we talk about the square root, we usually refer to the principal square root, which is the positive value (18).
-
Q: How can I calculate the square root of a number without a calculator?
- A: For smaller numbers, estimation and trial and error work well. For larger numbers, the Babylonian method or prime factorization are effective techniques. However, for very large numbers, advanced numerical methods are necessary.
-
Q: What is the difference between a square root and a cube root?
- A: The square root of a number is a value that, when multiplied by itself, gives the original number. A cube root is a value that, when multiplied by itself three times, gives the original number. For example, the cube root of 27 (∛27) is 3, because 3 x 3 x 3 = 27.
-
Q: Are there square roots for negative numbers?
- A: The square root of a negative number is not a real number. It's a complex number, involving the imaginary unit i, where i² = -1.
Conclusion: Beyond the Number 18
While the answer to the square root of 324 is simply 18, the journey to arrive at that answer has revealed a wealth of mathematical concepts and techniques. This exploration highlights the importance of understanding the underlying principles of mathematics, and how seemingly simple calculations can connect to complex and fascinating areas of study. The square root of 324 isn't just a number; it's a gateway to a deeper understanding of numerical relationships and the power of mathematical processes. From geometry to physics, and from algebra to engineering, the square root, and its application to numbers like 324, demonstrates its vital role in shaping our world and understanding the universe around us. The seemingly simple calculation offers a fascinating insight into the rich tapestry of mathematics.
Latest Posts
Latest Posts
-
Root System Of Mango
Sep 22, 2025
-
Micrograms To Ml Conversion
Sep 22, 2025
-
18 Gallon To Litres
Sep 22, 2025
-
Inch And 3 8
Sep 22, 2025
-
Lewis Dot For Water
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 324 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.