Square Root Of 325
renascent
Sep 24, 2025 · 6 min read
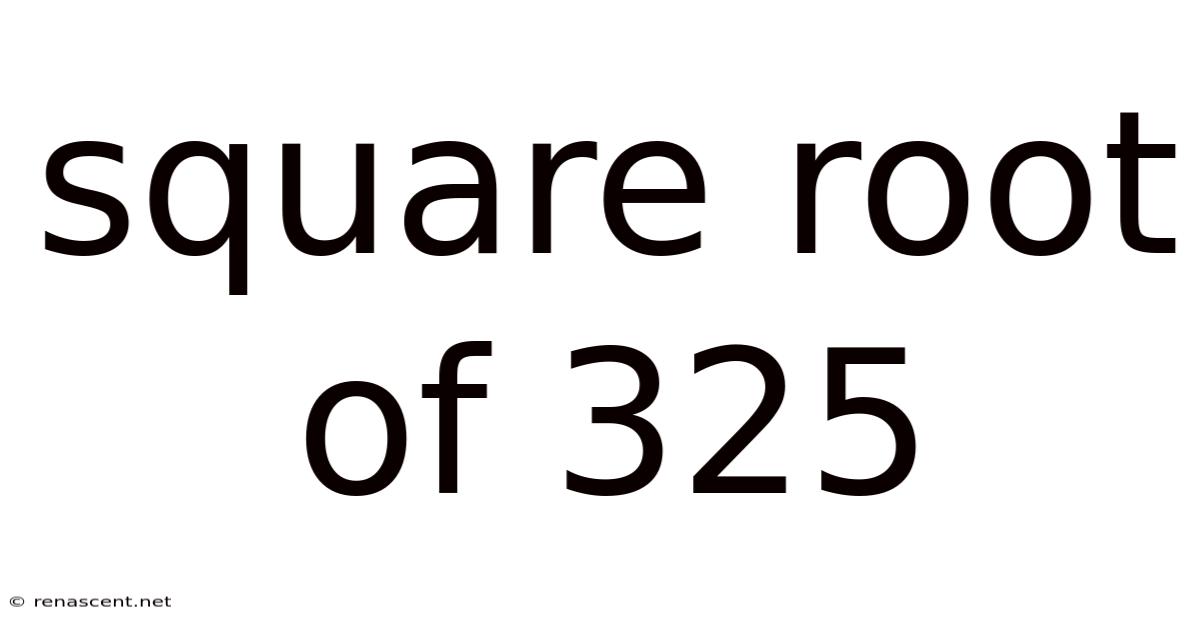
Table of Contents
Unveiling the Mysteries of the Square Root of 325: A Comprehensive Guide
Finding the square root of 325 might seem like a simple mathematical task, but delving deeper reveals fascinating connections to prime factorization, estimation techniques, and even the world of irrational numbers. This comprehensive guide will not only show you how to calculate √325 but also explore the underlying concepts, offering a deeper understanding of this fundamental mathematical operation. This exploration will equip you with the skills to tackle similar problems and appreciate the beauty of mathematics.
Understanding Square Roots: A Quick Recap
Before we dive into the specifics of √325, let's refresh our understanding of square roots. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. Square roots are the inverse operation of squaring a number.
The square root of 325, denoted as √325, is the number that, when multiplied by itself, equals 325. Unlike the square root of 9, which is a whole number, √325 is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Method 1: Prime Factorization and Simplification
The most elegant approach to simplifying the square root of 325 involves prime factorization. This method allows us to break down the number into its prime factors and then simplify the expression. Let's break down 325:
- Find the prime factors: We start by dividing 325 by the smallest prime number, 5: 325 ÷ 5 = 65.
- Continue factoring: Now we factor 65: 65 ÷ 5 = 13. 13 is a prime number.
- Express as prime factors: Therefore, the prime factorization of 325 is 5 x 5 x 13, or 5² x 13.
Now, we can rewrite √325 using the prime factors:
√325 = √(5² x 13)
Since √(a x b) = √a x √b, we can separate the factors:
√325 = √5² x √13
We know that √5² = 5, so we simplify to:
√325 = 5√13
This is the simplified radical form of √325. It's a much neater representation than the decimal approximation, and it preserves the exact value.
Method 2: Approximation using Estimation Techniques
While the simplified radical form (5√13) is precise, it’s not always practical. In many applications, an approximate decimal value is sufficient. We can use estimation techniques to get a reasonably accurate approximation of √325.
-
Find nearby perfect squares: Identify perfect squares close to 325. We know that 18² = 324 and 19² = 361. Since 325 is closer to 324 than 361, our approximation will be closer to 18.
-
Refine the estimation: We can use a linear approximation. The difference between 325 and 324 is 1. The difference between 361 and 324 is 37. Therefore, we can estimate that √325 is approximately 18 + (1/37). This gives us an approximation of roughly 18.027.
-
Using a calculator: For a more precise decimal approximation, we can use a calculator. The calculator will give you a value close to 18.0277563773.
Method 3: Using the Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative algorithm for approximating square roots. It's a powerful technique that refines the approximation with each iteration, converging towards the true value.
Here’s how it works for √325:
-
Make an initial guess: Let's start with our initial guess of 18, as we know it's close to the actual value.
-
Iterate using the formula: The formula for the Babylonian method is: x_(n+1) = 0.5 * (x_n + (N / x_n)), where x_n is the current guess, x_(n+1) is the next guess, and N is the number whose square root we're finding (325 in this case).
-
Repeat: We repeat this process, using the new guess as the input for the next iteration. Let's do a few iterations:
- Iteration 1: x_1 = 0.5 * (18 + (325 / 18)) ≈ 18.02777...
- Iteration 2: x_2 = 0.5 * (18.02777... + (325 / 18.02777...)) ≈ 18.0277563773
- Further iterations will yield increasingly accurate results.
The Significance of Irrational Numbers
As mentioned earlier, √325 is an irrational number. This means its decimal representation is non-terminating and non-repeating. Irrational numbers play a crucial role in mathematics, representing quantities that cannot be precisely expressed as a ratio of two integers. Their existence expands the number system beyond the rational numbers, providing a richer and more complete mathematical framework. The discovery and understanding of irrational numbers were significant milestones in the history of mathematics.
Practical Applications of Square Roots
Square roots are fundamental in many areas, including:
- Geometry: Calculating the lengths of sides in right-angled triangles using the Pythagorean theorem (a² + b² = c²).
- Physics: Solving problems involving motion, energy, and forces.
- Engineering: Designing structures and calculating distances.
- Statistics: Calculating standard deviation and other statistical measures.
- Computer graphics: Generating 2D and 3D images and animations.
Frequently Asked Questions (FAQ)
Q: Is there a way to calculate the square root without a calculator?
A: While a calculator provides the most accurate and efficient method, you can use estimation techniques, such as the Babylonian method, to approximate the square root without a calculator. However, these methods require iterative calculations.
Q: What is the difference between a perfect square and a non-perfect square?
A: A perfect square is a number that can be obtained by squaring a whole number (e.g., 9, 16, 25). A non-perfect square, like 325, is a number that cannot be obtained by squaring a whole number.
Q: Why is √325 an irrational number?
A: An irrational number cannot be expressed as a simple fraction (a/b, where a and b are integers and b ≠ 0). Because the prime factorization of 325 contains a prime factor (13) that is not squared, its square root cannot be expressed as a simple fraction, hence it's irrational.
Q: Can I simplify √325 further than 5√13?
A: No. 5√13 is the simplest radical form. You cannot simplify it further without resorting to a decimal approximation.
Conclusion
Calculating and understanding the square root of 325 provides a practical illustration of fundamental mathematical concepts. From prime factorization and simplification to estimation and iterative approximation methods, this seemingly simple calculation opens doors to a deeper appreciation of number theory, irrational numbers, and the power of mathematical techniques. Whether you need a precise value or a reasonable approximation, the methods explored in this guide equip you with the knowledge to tackle square root calculations effectively. Remember, the beauty of mathematics lies not only in the answers but also in the journey of discovery and understanding.
Latest Posts
Latest Posts
-
Life Expectancy For Niger
Sep 24, 2025
-
55 In A Fraction
Sep 24, 2025
-
77 Lbs To Kg
Sep 24, 2025
-
Lewis Structure For Methanol
Sep 24, 2025
-
The Hollow Men Explanation
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 325 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.