Whats 20 Of 80
renascent
Sep 22, 2025 · 5 min read
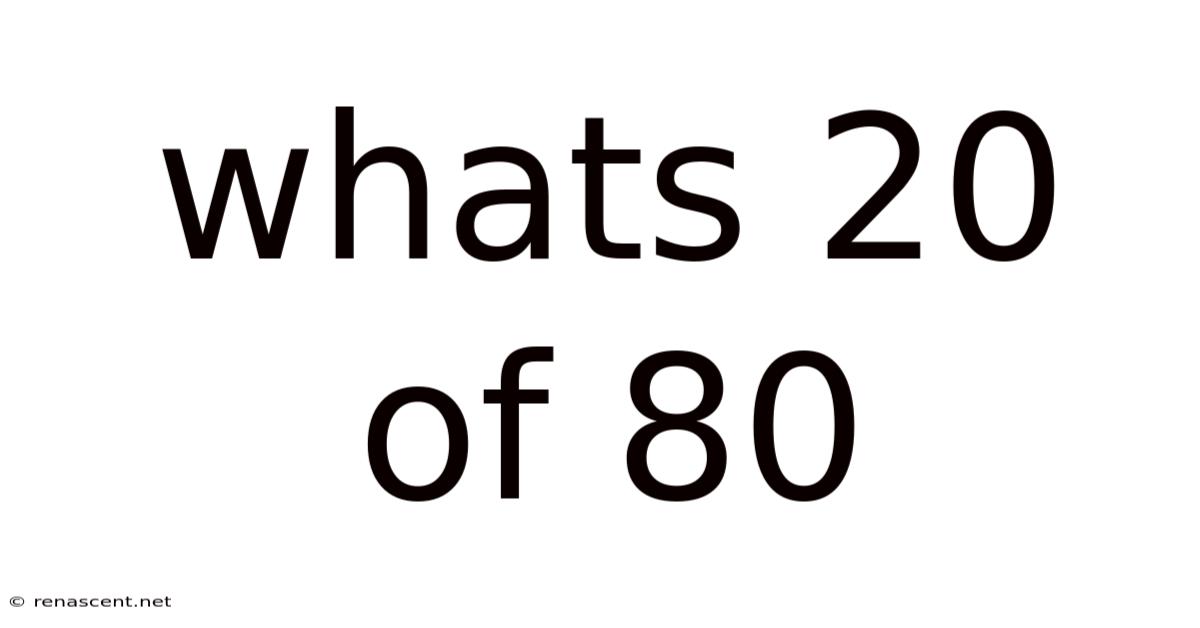
Table of Contents
What's 20% of 80? A Deep Dive into Percentages and Their Applications
Finding 20% of 80 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in everyday life. This article will not only answer the question directly but also explore the underlying principles of percentages, different methods for calculating them, and real-world examples showcasing their importance. We'll delve into the theoretical underpinnings and provide practical strategies to confidently tackle percentage calculations in various contexts.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." When we say "20%," we mean 20 parts out of 100 equal parts. This can be represented as a fraction (20/100) or a decimal (0.20).
Understanding this fundamental concept is crucial. It allows us to easily compare proportions and ratios, regardless of the original quantities involved. For example, comparing a 20% discount on a $100 item to a 10% discount on a $200 item becomes straightforward once we understand the underlying percentage representation.
Calculating 20% of 80: The Methods
There are several ways to calculate 20% of 80. Let's explore the most common methods:
Method 1: Using the Fraction Method
This method directly utilizes the fractional representation of a percentage. Since 20% is equivalent to 20/100, we can express the problem as:
(20/100) * 80
Simplifying the fraction to 1/5, we get:
(1/5) * 80 = 16
Therefore, 20% of 80 is 16.
Method 2: Using the Decimal Method
This method uses the decimal equivalent of the percentage. As mentioned earlier, 20% is equal to 0.20. The calculation becomes:
0.20 * 80 = 16
This method is often preferred for its ease of use with calculators.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the unknown value. We can set up the proportion as follows:
20/100 = x/80
Cross-multiplying, we get:
100x = 20 * 80
100x = 1600
x = 1600/100
x = 16
Again, we find that 20% of 80 is 16.
Beyond the Basic Calculation: Exploring Applications
The seemingly simple calculation of 20% of 80 has far-reaching implications in numerous fields:
1. Finance and Business:
- Discounts and Sales: Retailers frequently offer discounts expressed as percentages. Understanding percentage calculations allows consumers to quickly determine the actual price reduction. For example, a 20% discount on an $80 item is a saving of $16.
- Profit Margins: Businesses use percentages to calculate their profit margins – the difference between the cost of goods and the selling price, expressed as a percentage of the selling price.
- Interest Rates: Interest on loans and savings accounts is often calculated as a percentage of the principal amount. Understanding percentage calculations is essential for managing personal finances and making informed investment decisions.
- Taxes: Sales taxes, income taxes, and other taxes are often expressed as percentages of the taxable amount.
2. Science and Statistics:
- Data Analysis: Percentages are widely used to represent proportions and ratios in scientific data analysis. For example, a study might report that 20% of participants in a clinical trial experienced a specific side effect.
- Probability: Probability is often expressed as a percentage, indicating the likelihood of an event occurring. For example, there's a 20% chance of rain tomorrow.
3. Everyday Life:
- Tip Calculation: Calculating a tip in a restaurant often involves finding a percentage of the total bill. A 20% tip on an $80 meal would be $16.
- Recipe Scaling: When adjusting recipes, percentages can be used to increase or decrease ingredient quantities proportionally.
- Grading Systems: Many educational institutions use percentage-based grading systems to represent a student's performance on assessments.
Advanced Percentage Calculations: Going Further
While calculating 20% of 80 is relatively straightforward, understanding how to handle more complex percentage problems is crucial. Let's consider some common scenarios:
-
Finding the Original Amount: If you know that 20% of an unknown number is 16, how do you find the original number? You would set up the equation: 0.20 * x = 16, and solve for x (x = 16 / 0.20 = 80).
-
Calculating Percentage Increase or Decrease: Suppose a value increases from 80 to 100. To calculate the percentage increase, you first find the difference (100 - 80 = 20), then divide this difference by the original value (20 / 80 = 0.25), and finally multiply by 100 to express it as a percentage (0.25 * 100 = 25%). Similarly, you can calculate percentage decreases.
-
Compound Percentage Changes: In scenarios involving multiple percentage changes, the order of operations matters. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Percentage Points vs. Percentages: It's important to differentiate between percentage points and percentages. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase (10/20 *100 = 50%).
Frequently Asked Questions (FAQs)
Q1: What are some common mistakes people make when working with percentages?
A1: Common mistakes include: confusing percentage points with percentages, incorrectly calculating percentage increases or decreases, and not understanding the order of operations in compound percentage changes. Always double-check your work and ensure you are using the correct method for the specific problem.
Q2: Are there any online tools or calculators that can help with percentage calculations?
A2: Yes, many online calculators and tools are available to assist with percentage calculations. These can be helpful for quick calculations or for checking your work. However, understanding the underlying principles is crucial for solving more complex problems and applying percentage calculations to real-world scenarios.
Q3: How can I improve my understanding of percentages?
A3: Practice is key. Solve various percentage problems, starting with simple examples and gradually moving to more complex scenarios. Try working through real-world examples, such as calculating discounts, interest, or tips. If you struggle with a specific aspect, revisit the underlying concepts and seek further clarification from educational resources.
Conclusion
Calculating 20% of 80, while seemingly trivial, serves as a gateway to understanding a fundamental mathematical concept with widespread applications across diverse fields. Mastering percentage calculations empowers individuals to make informed decisions in finance, science, and everyday life. By understanding the different methods for calculating percentages and practicing various scenarios, you'll gain confidence and proficiency in handling percentage-related problems. Remember to always double-check your work and consider utilizing online tools when needed, but always prioritize understanding the core principles.
Latest Posts
Latest Posts
-
22 5 Pounds To Kg
Sep 22, 2025
-
121 Lb To Kg
Sep 22, 2025
-
12 Ounces To Kg
Sep 22, 2025
-
One Million One Hundred
Sep 22, 2025
-
How Long Till 10 35
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.