X 2 4x 2
renascent
Sep 14, 2025 · 6 min read
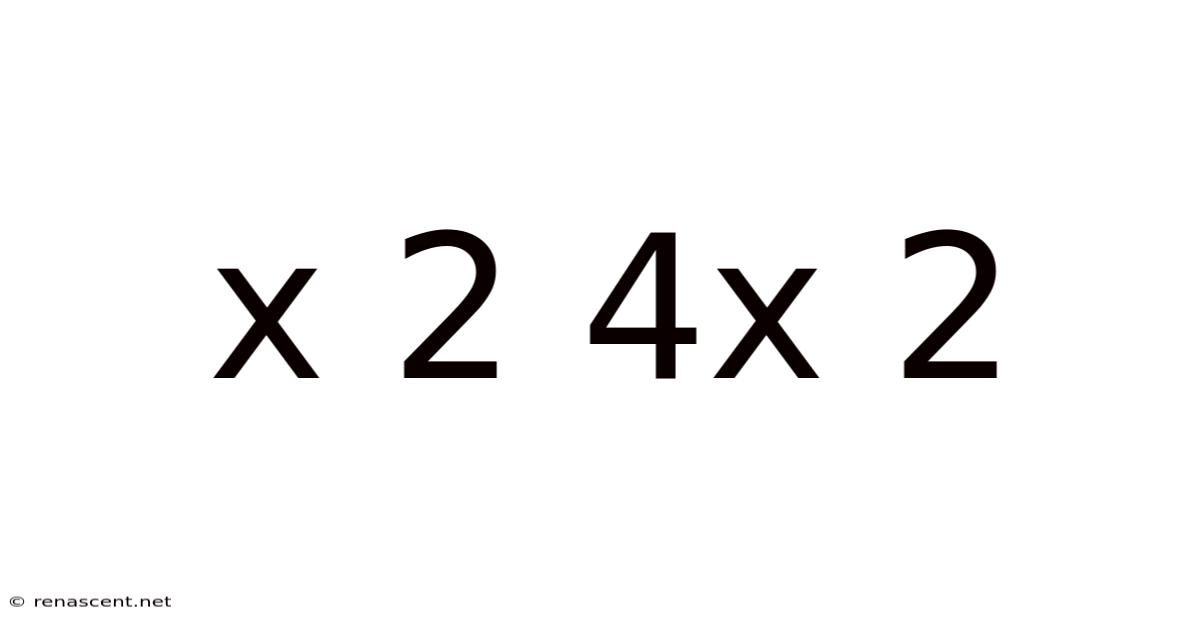
Table of Contents
Decoding x² + 4x + 2: A Deep Dive into Quadratic Equations
This article provides a comprehensive exploration of the quadratic expression x² + 4x + 2, covering its various aspects, from basic understanding to advanced applications. We'll delve into methods for solving it, analyzing its properties, and uncovering its relevance in various mathematical contexts. Understanding quadratic equations like this one is fundamental to many areas of mathematics and science.
Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where a, b, and c are constants, and a is not equal to zero. In our specific case, x² + 4x + 2, we have a = 1, b = 4, and c = 2.
This seemingly simple expression holds a wealth of mathematical properties and can be approached using several different methods. Let's explore these approaches in detail.
Methods for Solving Quadratic Equations
While the expression itself doesn't equate to anything (it's not an equation), if we set it equal to zero (x² + 4x + 2 = 0), we have a quadratic equation that we can solve to find the values of x that satisfy the equation. Here are the primary methods:
1. Factoring
Factoring involves expressing the quadratic expression as a product of two linear expressions. Unfortunately, x² + 4x + 2 cannot be easily factored using integers. We would need to find two numbers that add up to 4 (the coefficient of x) and multiply to 2 (the constant term). No such integer pair exists. This means we need to resort to other methods.
2. Completing the Square
Completing the square is a powerful technique that transforms the quadratic expression into a perfect square trinomial, plus a constant. This allows us to solve for x more easily.
Here's how it works for x² + 4x + 2:
- Group the x terms: (x² + 4x) + 2
- Find the value to complete the square: Take half of the coefficient of x (4/2 = 2), and square it (2² = 4).
- Add and subtract the value: (x² + 4x + 4) - 4 + 2
- Factor the perfect square trinomial: (x + 2)² - 2
- Set equal to zero (if solving an equation): (x + 2)² - 2 = 0
- Solve for x: (x + 2)² = 2 => x + 2 = ±√2 => x = -2 ± √2
Therefore, the solutions to the equation x² + 4x + 2 = 0 are x = -2 + √2 and x = -2 - √2. These are the roots or zeros of the quadratic equation.
3. Quadratic Formula
The quadratic formula provides a direct solution for any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our equation (x² + 4x + 2 = 0), a = 1, b = 4, and c = 2. Substituting these values into the formula gives:
x = [-4 ± √(4² - 4 * 1 * 2)] / (2 * 1) x = [-4 ± √(16 - 8)] / 2 x = [-4 ± √8] / 2 x = [-4 ± 2√2] / 2 x = -2 ± √2
This confirms the solutions we obtained using completing the square.
Analyzing the Quadratic Expression: Properties and Graph
The quadratic expression x² + 4x + 2 represents a parabola when graphed on a Cartesian coordinate system. Let's explore some of its key properties:
-
Vertex: The vertex represents the minimum or maximum point of the parabola. For a quadratic in the form ax² + bx + c, the x-coordinate of the vertex is given by -b/2a. In our case: -4 / (2 * 1) = -2. The y-coordinate is found by substituting the x-coordinate back into the expression: (-2)² + 4(-2) + 2 = -2. Therefore, the vertex is (-2, -2).
-
Axis of Symmetry: The parabola is symmetric around a vertical line passing through its vertex. The equation of the axis of symmetry is x = -2.
-
x-intercepts (Roots): These are the points where the parabola intersects the x-axis. We already found these using the quadratic formula: x = -2 + √2 and x = -2 - √2.
-
y-intercept: This is the point where the parabola intersects the y-axis. It's found by setting x = 0 in the expression: 0² + 4(0) + 2 = 2. The y-intercept is (0, 2).
-
Concavity: Since the coefficient of x² (a = 1) is positive, the parabola opens upwards (it's a U-shape). If a were negative, it would open downwards.
Understanding these properties allows us to accurately sketch the graph of the parabola represented by x² + 4x + 2.
Applications of Quadratic Equations
Quadratic equations and their related expressions have wide-ranging applications in various fields:
-
Physics: Projectile motion, where the trajectory of an object is often described by a quadratic equation.
-
Engineering: Designing curves, bridges, and other structures.
-
Economics: Modeling cost, revenue, and profit functions.
-
Computer Graphics: Creating curved lines and shapes.
-
Statistics: Analyzing data and fitting curves to datasets.
Frequently Asked Questions (FAQ)
Q: Can all quadratic equations be solved by factoring?
A: No. While factoring is a useful method, many quadratic equations, including x² + 4x + 2 = 0, cannot be easily factored using integers. The quadratic formula and completing the square are more general methods that work for all quadratic equations.
Q: What does the discriminant (b² - 4ac) tell us?
A: The discriminant in the quadratic formula indicates the nature of the roots:
- If b² - 4ac > 0, there are two distinct real roots.
- If b² - 4ac = 0, there is one real root (a repeated root).
- If b² - 4ac < 0, there are two complex roots (involving imaginary numbers).
For x² + 4x + 2, the discriminant is 16 - 8 = 8 > 0, indicating two distinct real roots.
Q: How can I graph a quadratic equation?
A: You can graph a quadratic equation by plotting its key features: the vertex, the axis of symmetry, the x-intercepts, and the y-intercept. You can also use a graphing calculator or software. Knowing the concavity (upward or downward opening) also helps in sketching the graph accurately.
Conclusion
The seemingly simple quadratic expression x² + 4x + 2 opens a window into the rich world of quadratic equations. Through methods like completing the square and the quadratic formula, we can solve the corresponding equation and understand its properties. The graph of this expression is a parabola with specific characteristics that can be analyzed to understand its behavior. The ability to manipulate and solve quadratic equations is a cornerstone of mathematical understanding, with applications extending far beyond the classroom. This deep dive reveals the power and elegance of this fundamental mathematical concept. Remember, continued practice and exploration will solidify your understanding and allow you to apply these concepts confidently in various contexts.
Latest Posts
Latest Posts
-
Highest Recorded Bac Ever
Sep 14, 2025
-
25 Percent Of 19
Sep 14, 2025
-
100 2 F To C
Sep 14, 2025
-
Mesoamerica And The Andes
Sep 14, 2025
-
Seafoam Islands Infinite Fusion
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 2 4x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.