X 3 2x 2
renascent
Sep 18, 2025 · 6 min read
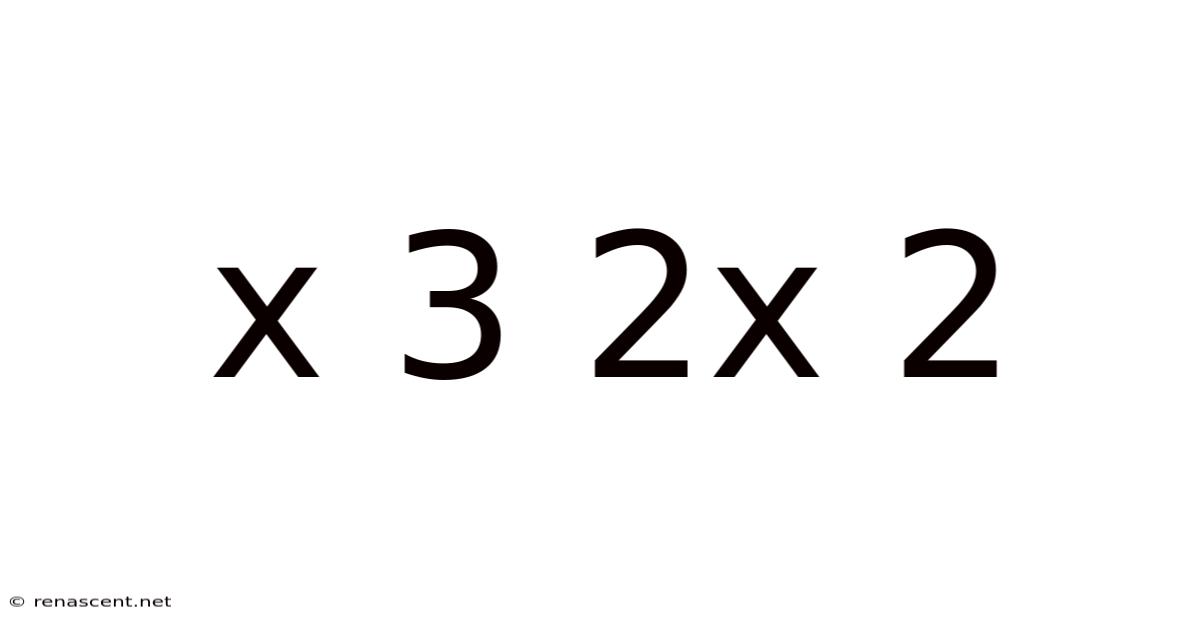
Table of Contents
Decoding the Mystery: A Deep Dive into x³ - 2x²
This article explores the mathematical expression x³ - 2x², delving into its properties, analysis, and applications. We'll cover various aspects, from basic factorization and graphing to more advanced concepts like finding roots and exploring its behavior in calculus. Understanding this seemingly simple expression reveals fundamental principles in algebra and beyond. This comprehensive guide is designed for students and enthusiasts alike, offering a clear, step-by-step understanding of this cubic polynomial.
Understanding the Fundamentals: Factoring and Simplification
At its core, x³ - 2x² is a cubic polynomial, meaning it's a polynomial expression with the highest power of x being 3. The first step in understanding any polynomial is to simplify and factor it if possible. In this case, we can factor out the greatest common factor (GCF) which is x².
This gives us:
x³ - 2x² = x²(x - 2)
This factored form is incredibly useful. It immediately tells us two crucial pieces of information:
- One root: Setting the expression equal to zero, we find one solution (or root) is x = 0. This is because if x² = 0, then x = 0.
- Another root: Setting (x - 2) = 0 gives us another root, x = 2.
These roots represent the x-intercepts of the graph of the function y = x³ - 2x².
Graphing the Cubic Polynomial: A Visual Representation
Visualizing the function is crucial for understanding its behavior. The graph of y = x³ - 2x² exhibits a characteristic shape of a cubic function. It will have:
- x-intercepts: At x = 0 and x = 2, as we found from the factored form.
- y-intercept: When x = 0, y = 0. Therefore, the y-intercept is also at the origin (0,0).
- Turning points: Cubic functions can have up to two turning points (local maxima or minima). In this case, we can find these points using calculus (discussed later). Intuitively, we can see that there will be a change in the slope of the curve around x=0. It will likely have a local minimum near x=0 and increase thereafter.
Sketching the graph, we see a curve that passes through (0,0) and (2,0), showing the roots we identified earlier. The curve starts from the bottom left quadrant, passes through the origin, and then through the x-axis again at x=2 before increasing towards positive infinity.
Exploring the Behavior with Calculus: Derivatives and Turning Points
Calculus provides powerful tools to analyze the behavior of the function in more detail. Let's explore the first and second derivatives:
First Derivative: The first derivative, f'(x), tells us about the slope of the function at any given point. For f(x) = x³ - 2x², we have:
f'(x) = 3x² - 4x
Setting f'(x) = 0 allows us to find the critical points, where the slope is zero (potential turning points).
3x² - 4x = 0 x(3x - 4) = 0
This gives us two critical points: x = 0 and x = 4/3.
Second Derivative: The second derivative, f''(x), tells us about the concavity of the function (whether it's curving upwards or downwards). For our function:
f''(x) = 6x - 4
- At x = 0, f''(0) = -4 (concave down – a local maximum). However, in this case, it is not a global maximum, and the function tends towards negative infinity.
- At x = 4/3, f''(4/3) = 4 (concave up – a local minimum).
Therefore, the graph has a local minimum at x = 4/3. This confirms our earlier intuitive observation about the graph's shape. By calculating the y-coordinate at x = 4/3, we can pinpoint the exact location of this minimum point.
y = (4/3)³ - 2(4/3)² = -64/27 ≈ -2.37
Applications and Further Exploration
The expression x³ - 2x² finds application in various fields, including:
- Physics: It can model certain physical phenomena, such as the trajectory of a projectile or the rate of change of a quantity. The roots can represent significant points in these processes.
- Engineering: In engineering design, this type of expression might model the stress or strain on a structure.
- Economics: It can represent a cost function or a profit function, allowing analysis of optimal production levels.
Further exploration of x³ - 2x² could involve:
- Solving inequalities: Finding the intervals where x³ - 2x² > 0 or x³ - 2x² < 0. This involves analyzing the sign of the function across the intervals determined by its roots.
- Integration: Finding the indefinite integral of x³ - 2x², which provides valuable insights into the area under the curve.
- Complex roots: While we have only found real roots so far, exploring the possibility of complex roots (involving imaginary numbers) could provide a more complete understanding of the polynomial.
- Transformations: Exploring the effects of transformations, such as shifting the graph horizontally or vertically, or scaling the graph.
Frequently Asked Questions (FAQ)
Q: What is the degree of the polynomial x³ - 2x²?
A: The degree of the polynomial is 3, because the highest power of x is 3.
Q: How many roots does a cubic polynomial have?
A: A cubic polynomial can have up to three roots, which can be real or complex. In this case, we found two real roots (0 and 2). There could be one more complex root.
Q: What is the difference between a local minimum and a global minimum?
A: A local minimum is a point where the function value is smaller than its neighbors, while a global minimum is the absolute lowest point of the function over its entire domain.
Q: Can this polynomial be factored further than x²(x-2)?
A: No, this is the complete factorization over the real numbers. It contains no other factors that can be easily found.
Q: How can I find the complex roots (if any) of this polynomial?
A: Finding complex roots often involves using more advanced techniques like the cubic formula or numerical methods. Since the polynomial is already factored, however, it is easy to see that there are only two real roots.
Conclusion: A Foundation for Further Learning
The exploration of x³ - 2x² serves as a microcosm of the broader world of polynomial analysis. Through factorization, graphing, and calculus, we've uncovered its key properties and applications. Understanding this seemingly simple expression provides a strong foundation for tackling more complex polynomial expressions and other mathematical concepts. Remember, the journey of understanding mathematics is a process of continuous exploration and discovery. The seemingly simple always hides layers of deeper knowledge waiting to be unveiled. This exploration should spark your curiosity and encourage you to delve deeper into the fascinating world of mathematics. Don't hesitate to explore further applications and related concepts to expand your mathematical knowledge.
Latest Posts
Latest Posts
-
214 Pounds To Kg
Sep 18, 2025
-
85 Mph In Kmh
Sep 18, 2025
-
52 Degrees Centigrade Fahrenheit
Sep 18, 2025
-
Best Novel First Lines
Sep 18, 2025
-
166 Minutes In Hours
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 3 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.