X 4 X 2
renascent
Sep 14, 2025 · 7 min read
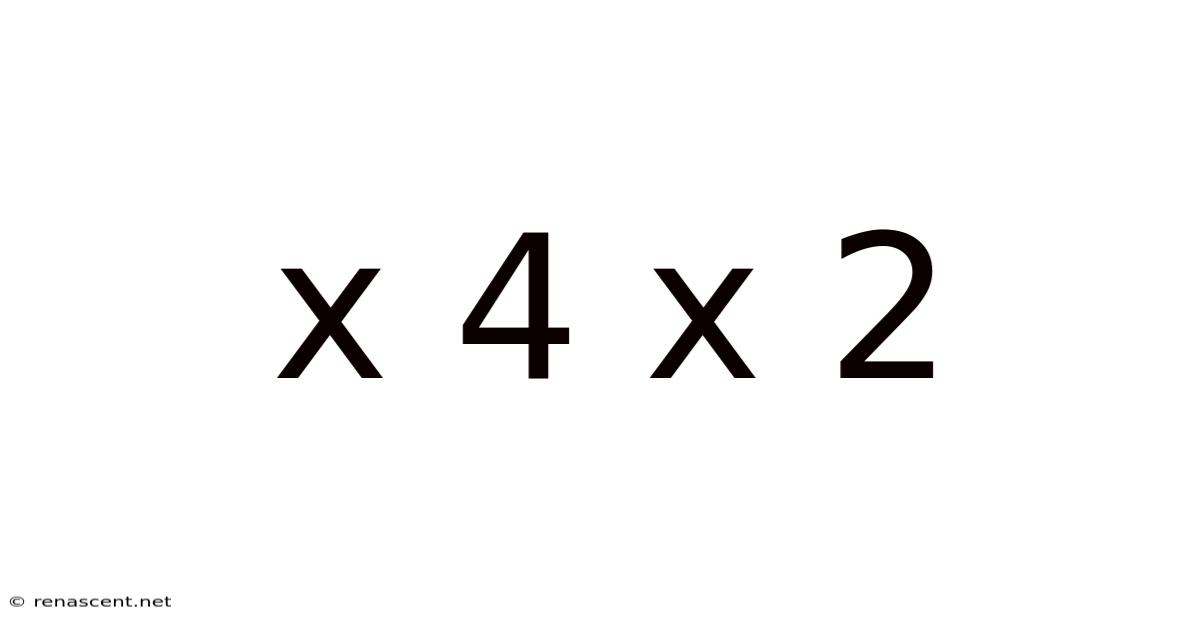
Table of Contents
Decoding the Mystery: A Deep Dive into X x 4 x 2
The seemingly simple expression "X x 4 x 2" can represent a surprisingly vast landscape of mathematical concepts and practical applications. This article will explore this expression from its fundamental arithmetic operations to its advanced implications in algebra, geometry, and beyond. We'll unpack its meaning, delve into its practical uses, and address common questions surrounding its interpretation and manipulation. Understanding this seemingly basic equation opens doors to a wider comprehension of mathematical reasoning.
Understanding the Basics: Multiplication and Order of Operations
At its core, "X x 4 x 2" is a multiplication problem. Multiplication is a fundamental arithmetic operation that represents repeated addition. In this case, we're multiplying an unknown variable, X, by 4, and then multiplying the result by 2.
The crucial element here is the order of operations. In mathematics, we follow the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) to ensure consistent results. Since there are no parentheses or exponents in our expression, we perform multiplication from left to right. This means we first multiply X by 4, resulting in 4X, and then multiply that result by 2, giving us 8X.
Therefore, the simplified form of "X x 4 x 2" is 8X. This seemingly simple simplification holds the key to understanding more complex problems.
Algebraic Applications: Solving for X
The expression "8X" is an algebraic term. Algebra involves using symbols, such as X, to represent unknown values. The beauty of simplifying "X x 4 x 2" to "8X" lies in its use for solving equations.
Let's imagine we have the equation: X x 4 x 2 = 24.
Using our simplified expression, we can rewrite this equation as: 8X = 24.
To solve for X, we need to isolate X on one side of the equation. We achieve this by dividing both sides of the equation by 8:
8X / 8 = 24 / 8
This simplifies to:
X = 3
Therefore, in this specific instance, the value of X that satisfies the equation X x 4 x 2 = 24 is 3. This demonstrates the power of simplification in solving algebraic equations. The ability to simplify complex expressions is a cornerstone of algebraic manipulation.
Geometric Interpretations: Area and Volume
The expression "X x 4 x 2" can also have geometric interpretations, particularly when dealing with area and volume calculations. Imagine a rectangular prism (a box).
-
Area of a Rectangle: If X represents the length of a rectangle and 4 represents its width, then X x 4 represents the area of that rectangle. Multiplying the result by 2 could represent the area of two identical rectangles stacked on top of each other.
-
Volume of a Rectangular Prism: If X represents the length, 4 represents the width, and 2 represents the height of a rectangular prism, then X x 4 x 2 represents the volume of that prism. The volume is a three-dimensional measure encompassing length, width, and height.
Understanding this connection bridges the gap between abstract algebraic expressions and concrete geometric representations. The ability to visualize mathematical concepts is crucial for a deeper understanding.
Practical Applications Across Disciplines
The simple expression "X x 4 x 2" and its simplified form, 8X, have surprisingly broad applications across numerous disciplines:
-
Engineering: Calculating the total load-bearing capacity of a structure might involve multiplying several factors together, mirroring the structure of our expression. The variable X could represent an unknown structural element's strength.
-
Finance: Calculating compound interest over two periods could involve a similar structure. X might represent the principal amount, 4 a growth factor, and 2 the number of periods.
-
Physics: In physics, many equations involve multiplying several factors to determine a final result. Our expression could represent a simplified model for calculating force, momentum, or energy.
-
Computer Science: In programming, the expression could be part of a loop or algorithm, where X might be a counter or an input value. The multiplication operations would determine the final output based on the algorithm's logic.
These examples demonstrate that even a seemingly simple mathematical expression finds its relevance in diverse and complex real-world scenarios.
Advanced Considerations: Functions and Variables
The concept of X in "X x 4 x 2" can be further explored through the lens of functions and variables.
-
Functions: We can express "X x 4 x 2" as a function, f(X) = 8X. This function takes an input value (X) and produces an output value (8X). The function's linearity implies a direct proportional relationship between the input and output.
-
Variables and Constants: X is a variable, meaning its value can change. 4 and 2 are constants, meaning their values remain fixed. Understanding this distinction is critical in more advanced mathematical contexts. Manipulating variables and constants is fundamental to solving equations and interpreting mathematical relationships.
This deeper analysis emphasizes the multifaceted nature of even the simplest mathematical expression. It highlights the interconnectedness of various mathematical concepts and their role in solving more complex problems.
Extending the Concept: Polynomials and Beyond
Building upon the foundation of "X x 4 x 2," we can explore more complex expressions. Introducing additional terms and exponents leads us into the realm of polynomials. For example:
2X² + 8X + 5
This is a polynomial expression. The term "8X" (derived from our original expression) is a part of this larger, more intricate expression. Understanding the basics of "X x 4 x 2" lays the groundwork for comprehending and manipulating more advanced polynomial expressions. Mastering simpler concepts builds the foundation for exploring higher-level mathematics.
Frequently Asked Questions (FAQ)
Q: What if the order of multiplication is changed? Does it matter?
A: Yes, the order of multiplication matters in some contexts. While the commutative property of multiplication allows us to rearrange the order (X x 2 x 4), maintaining the order is crucial for understanding the underlying context and geometric interpretations. For instance, changing the order in a volume calculation might alter the interpretation of length, width, and height.
Q: Can X be a negative number?
A: Yes, X can be a negative number. The result will simply be a negative multiple of 8. For example, if X = -2, then 8X = -16. Understanding the handling of negative numbers is essential in mathematics.
Q: How does this relate to other mathematical operations like addition and subtraction?
A: This expression primarily involves multiplication. However, it can be incorporated into larger expressions involving addition and subtraction. For example, 8X + 5 or 8X - 10. Understanding the order of operations (PEMDAS) is crucial for correctly evaluating these more complex expressions.
Q: What are some real-world examples beyond the ones mentioned?
A: Numerous real-world scenarios can be modeled using this expression. Calculating the total cost of items with a quantity of 4 and a unit price of 2X, estimating the total distance traveled if you repeat a journey four times and each journey covers 2X kilometers, or calculating the total amount of ingredients needed for a recipe that requires a certain amount (2X) of base ingredients used four times. The applications are virtually limitless.
Conclusion: The Unassuming Power of 8X
The deceptively simple expression "X x 4 x 2," when simplified to 8X, reveals a wealth of mathematical concepts and practical applications. From solving algebraic equations to visualizing geometric shapes and understanding functions, this expression serves as a foundational building block for more advanced mathematical exploration. The journey from a simple arithmetic expression to its advanced implications highlights the interconnectedness of mathematical ideas and their far-reaching impact across various disciplines. Understanding this seemingly basic equation empowers us to tackle more complex problems with confidence and insight. Its simplicity masks its power and its ability to serve as a stepping stone towards more advanced mathematical concepts. The ability to simplify and interpret such expressions is crucial for anyone looking to strengthen their mathematical foundation.
Latest Posts
Latest Posts
-
2 500 Kg To Lbs
Sep 15, 2025
-
186 5 Cm In Feet
Sep 15, 2025
-
Text Structure Informational Text
Sep 15, 2025
-
157 Lbs To Kg
Sep 15, 2025
-
35 Divided By 5
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.