X 6 X 5
renascent
Sep 14, 2025 · 6 min read
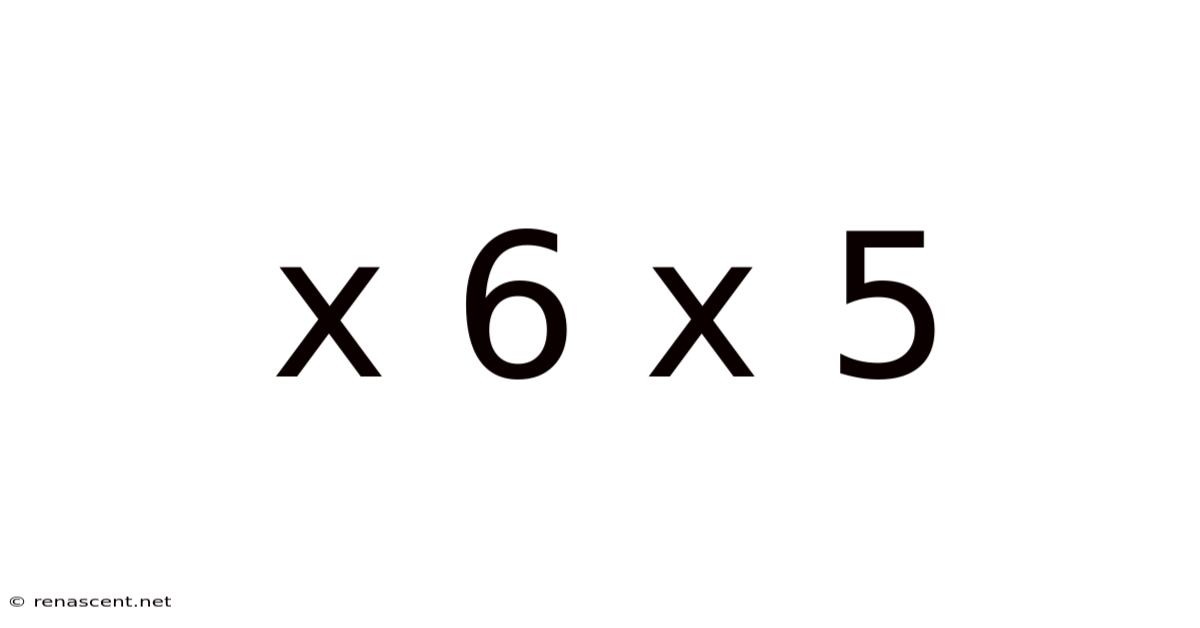
Table of Contents
Decoding the Enigma: A Deep Dive into the Mathematical World of 6 x 5 x X
The seemingly simple expression "6 x 5 x X" might appear straightforward at first glance. However, this seemingly basic arithmetic equation opens a doorway to a surprisingly vast landscape of mathematical concepts, applications, and interpretations. This article will explore the multiple facets of this expression, delving into its fundamental arithmetic, its algebraic implications, its potential real-world applications, and addressing common questions surrounding its interpretation. Understanding 6 x 5 x X isn't just about finding a numerical answer; it's about grasping the underlying principles of mathematics and their versatility.
Understanding the Fundamentals: Basic Arithmetic
Let's begin with the most fundamental interpretation: treating "X" as an unknown variable requiring a numerical value. In this case, "6 x 5 x X" represents a simple multiplication problem. The first step involves solving the known multiplication: 6 multiplied by 5 equals 30. Therefore, the expression simplifies to "30 x X".
To find a definitive numerical answer, we need a value for X. If, for example, X = 2, then the expression becomes 30 x 2 = 60. If X = 10, the solution is 30 x 10 = 300. The beauty of this equation lies in its adaptability; the answer changes dynamically based on the value assigned to X. This highlights the importance of variables in mathematics – they represent unknown quantities that can take on different values depending on the context.
Algebraic Exploration: Unveiling the Power of X
Moving beyond basic arithmetic, "6 x 5 x X" allows us to explore the fundamentals of algebra. In algebra, "X" represents an unknown or a variable. This variable can represent various quantities, making algebraic equations highly versatile tools for solving problems in various fields.
The expression can be rewritten in a more conventional algebraic form: 30X = Y (where Y represents the final result). This equation represents a linear relationship between X and Y. Graphically, this equation would represent a straight line passing through the origin (0,0) with a slope of 30. This simple linear equation forms the foundation for many more complex algebraic concepts. Understanding this basic relationship is crucial for grasping more advanced algebraic manipulations and problem-solving.
We can also manipulate this equation. For instance, if we know the final result (Y), we can solve for X: X = Y/30. This allows us to determine the value of the unknown variable based on the outcome. This demonstrates the power of algebraic manipulation in solving for unknowns.
Real-World Applications: From Simple Calculations to Complex Models
The seemingly simple "6 x 5 x X" equation has numerous applications in diverse real-world scenarios. Let's consider a few examples:
-
Calculating Area: Imagine you're calculating the area of a rectangular prism. If the length is 6 units, the width is 5 units, and the height is represented by X units, then the volume of the prism is given by 6 x 5 x X cubic units. This equation allows us to calculate the volume given the height.
-
Cost Calculation: Consider a scenario where you are buying items. Each item costs $6, and you buy 5 items. If X represents the cost of an additional type of item, the total cost would be 6 x 5 + X dollars. This illustrates how the equation can be adapted to incorporate additional factors.
-
Production Rates: Let's say a factory produces 6 units of a product per hour, and operates for 5 hours. If X represents an additional production rate from a second machine, the total production for the day would be 6 x 5 + X units. This is a simple example of how this equation could model production rates within a larger system.
-
Scientific Modeling: While this specific equation may not be used directly in complex scientific models, the principles behind it—using variables to represent unknown quantities and performing mathematical operations to find solutions—are fundamental to all scientific modeling. Whether it's calculating the trajectory of a projectile or predicting population growth, the ability to manipulate variables and equations is essential.
Expanding the Possibilities: Beyond Simple Multiplication
The expression "6 x 5 x X" can be extended to incorporate more complex mathematical concepts.
-
Exponents: The equation could be rewritten as (6 x 5)X<sup>n</sup> where 'n' represents an exponent. This introduces the concept of exponential growth or decay, which has significant applications in various fields, including finance, biology, and physics.
-
Functions: The equation can be represented as a function: f(X) = 30X. This allows for a more formal mathematical representation and enables us to explore properties of this function, such as its domain, range, and continuity.
-
Calculus: While beyond the scope of this basic analysis, the principles underlying this equation become crucial in calculus. The concept of rate of change, integral calculus, and differential equations all build upon these fundamental algebraic manipulations and the use of variables.
Frequently Asked Questions (FAQ)
Here are some frequently asked questions about the expression "6 x 5 x X":
Q: What is the importance of the variable X?
A: The variable X represents an unknown quantity. Its presence makes the equation versatile, allowing it to represent a range of situations and solve for different values depending on the context.
Q: Can X be a negative number?
A: Yes, X can be a negative number. The result of the equation will then also be negative. This is a fundamental aspect of algebra.
Q: Can X be zero?
A: Yes, if X = 0, then the entire expression equals zero (6 x 5 x 0 = 0).
Q: Can X be a fraction or decimal?
A: Yes, X can be any real number, including fractions and decimals. The result will be the product of 30 and the value of X.
Q: What if we replace the multiplication with another operation?
A: Changing the operation would significantly alter the meaning and the solution. If we used addition (6 + 5 + X), or subtraction (6 - 5 - X), the outcome would be completely different and the mathematical principles involved would be different as well.
Conclusion: The Unfolding Potential of a Simple Equation
The seemingly simple equation "6 x 5 x X" serves as a gateway to a world of mathematical concepts and applications. From basic arithmetic to algebraic manipulation, and from simple real-world calculations to the foundations of advanced mathematical modeling, this equation highlights the power of variables, the versatility of mathematical operations, and the underlying principles that govern various aspects of our world. Understanding this expression is not just about finding a numerical answer; it's about grasping the fundamental concepts that underpin numerous mathematical and scientific endeavors. The more we explore this seemingly simple equation, the richer our understanding of mathematics becomes, revealing a depth and complexity that belies its initial appearance. It encourages us to delve deeper, question assumptions, and appreciate the power of mathematical thinking in solving diverse problems.
Latest Posts
Latest Posts
-
186 5 Cm In Feet
Sep 15, 2025
-
Text Structure Informational Text
Sep 15, 2025
-
157 Lbs To Kg
Sep 15, 2025
-
35 Divided By 5
Sep 15, 2025
-
Micron To Mm Conversion
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 6 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.