X 9 X 2
renascent
Sep 16, 2025 · 6 min read
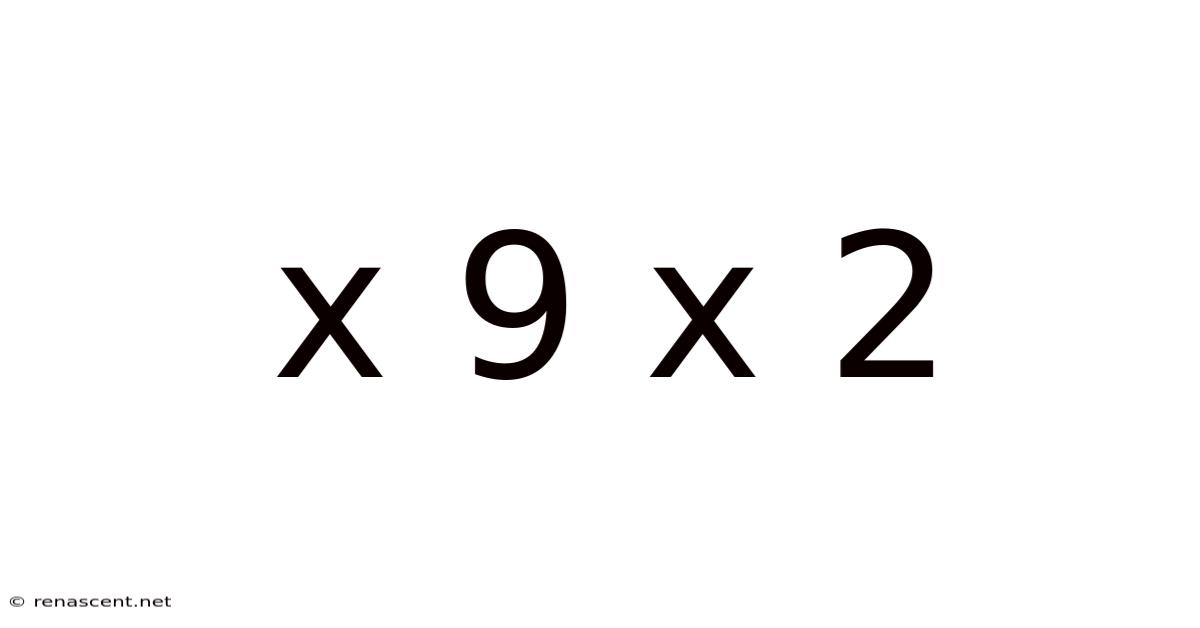
Table of Contents
Decoding the Mystery of X 9 X 2: A Deep Dive into Multiplication, Algebra, and Problem-Solving
This article explores the seemingly simple expression "x 9 x 2," delving far beyond its basic arithmetic interpretation. We'll uncover its potential as a gateway to understanding fundamental mathematical concepts, including multiplication, algebraic manipulation, and problem-solving strategies. Whether you're a student grappling with early algebra or an adult looking to refresh your mathematical skills, this comprehensive guide will illuminate the multifaceted nature of this expression.
Introduction: Beyond Simple Multiplication
At first glance, "x 9 x 2" appears straightforward: a simple multiplication problem. We multiply the variable x by 9, and then multiply the result by 2. But this seemingly uncomplicated expression offers a springboard for exploring more complex mathematical ideas. We'll dissect its meaning, analyze its potential variations, and examine its applications in different mathematical contexts. We'll also explore how to solve for x given different scenarios and how to interpret the results. This journey will strengthen your understanding of core mathematical principles and sharpen your problem-solving abilities.
Understanding the Fundamentals: Multiplication and the Order of Operations
Before diving into the complexities, let's solidify the basics. The expression "x 9 x 2" involves the fundamental arithmetic operation of multiplication. Multiplication is simply repeated addition. For example, 3 x 2 is the same as 3 + 3 = 6. In our expression, x is multiplied by 9, resulting in 9x, and then this result is multiplied by 2, yielding 18x.
Crucially, the order of operations (often remembered by the acronym PEMDAS/BODMAS – Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) dictates that multiplication is performed from left to right unless parentheses or brackets indicate otherwise. Therefore, there's no ambiguity in the order of calculations in "x 9 x 2."
Algebraic Manipulation: Solving for X
The true power of "x 9 x 2" lies in its algebraic potential. The presence of the variable x transforms this from a simple arithmetic problem into an algebraic equation. The expression can be simplified to 18x. However, to fully understand its significance, we need to consider different scenarios:
-
Scenario 1: Finding the value of the expression given a value for x. If we're given a specific value for x (e.g., x = 5), we can substitute this value into the expression: 5 x 9 x 2 = 90. This demonstrates the direct application of the expression for evaluating numerical outcomes.
-
Scenario 2: Solving for x given the value of the expression. This involves a bit more algebraic manipulation. Let's say the entire expression equals 36. Then we have the equation 18x = 36. To solve for x, we divide both sides of the equation by 18: x = 36/18 = 2. This showcases the process of isolating the variable to find its value.
-
Scenario 3: Understanding the Relationship between x and the Expression's Value. The expression 18x illustrates a direct proportional relationship between x and the overall value. As x increases, the value of the expression increases proportionally. This relationship is crucial for understanding the behavior of linear functions.
Expanding the Scope: Applications in Different Mathematical Contexts
The simplicity of "x 9 x 2" belies its broader applications within various mathematical disciplines:
-
Linear Equations: The expression is a fundamental component of linear equations. Linear equations are equations of the form y = mx + c, where 'm' represents the slope and 'c' represents the y-intercept. Our expression, 18x, is a linear equation with a slope of 18 and a y-intercept of 0. Understanding this relationship allows for graphing the equation, identifying key points, and analyzing its properties.
-
Functions and Mappings: We can view "x 9 x 2" as a function, f(x) = 18x. A function maps an input value (x) to an output value (18x). This concept is crucial in higher-level mathematics, such as calculus and analysis.
-
Geometry and Area Calculation: Imagine a rectangle with a width of 9 units and a length represented by x units. The area of this rectangle would be 9x square units. Multiplying this area by 2 (perhaps representing two identical rectangles), gives us a total area of 18x square units. This example showcases the applicability of the expression in geometric problems.
-
Problem Solving and Word Problems: The expression can form the basis of various word problems. For instance, "A factory produces 9 units of a product per hour. If the factory operates for x hours and doubles its production for a special order, how many units are produced?" The answer is expressed using "x 9 x 2" which equates to 18x units.
Visualizing the Expression: Graphing Linear Equations
Graphing the equation y = 18x provides a powerful visual representation of the relationship between x and the expression's value. The graph will be a straight line passing through the origin (0,0) with a steep positive slope. This visual representation helps to understand the concept of proportionality and the behaviour of linear functions. Each point on the line represents a specific x-value and its corresponding value for 18x.
Advanced Concepts: Expanding the Expression
While we've focused on the basic form "x 9 x 2," we can expand the concept to explore more complex scenarios:
-
Introducing additional variables: The expression could be modified to include other variables, such as "x 9 y 2," creating a more complex algebraic expression requiring a deeper understanding of variable manipulation.
-
Incorporating exponents: Adding exponents, like "x² 9 x 2", introduces quadratic equations, requiring different solution methods (e.g., factoring, quadratic formula).
-
Including Parentheses or Brackets: Adding parentheses alters the order of operations. For example, "(x + 2) 9 x 2" necessitates solving the parentheses first before performing the multiplications.
Frequently Asked Questions (FAQ)
-
What if the order of multiplication is changed? While mathematically equivalent, altering the order, for instance, to "2 x 9 x x", will still result in the simplified expression 18x. However, for the sake of clarity and consistency, it's recommended to maintain the initial order.
-
Can x be a negative number? Yes, x can be a negative number. The expression will still yield a valid result, though the result will also be negative. For example, if x = -3, then x 9 x 2 = -54.
-
What are the practical applications of this expression beyond mathematics? The underlying concepts of multiplication, proportion, and algebraic manipulation have extensive real-world applications in various fields, including engineering, finance, physics, and computer science, amongst others.
Conclusion: Unlocking the Potential of "x 9 x 2"
While seemingly simple, "x 9 x 2" serves as a powerful tool for understanding fundamental mathematical concepts. Its analysis extends beyond basic arithmetic to encompass algebraic manipulation, function analysis, and problem-solving strategies. By exploring its variations and applications within different mathematical contexts, we've uncovered its multifaceted nature. Mastering this seemingly basic expression lays a strong foundation for tackling more complex mathematical challenges in the future. Remember, even the simplest mathematical concepts can reveal profound insights when explored thoroughly. Continue to question, investigate, and explore the fascinating world of mathematics. The journey of mathematical understanding is continuous and rewarding.
Latest Posts
Latest Posts
-
6 Lbs 1 Oz
Sep 16, 2025
-
73 5 Kg To Pounds
Sep 16, 2025
-
1 66 M In Feet
Sep 16, 2025
-
Mac Address From Ping
Sep 16, 2025
-
5250 Divided By 2
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 9 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.