X2 X 3 0
renascent
Sep 13, 2025 · 5 min read
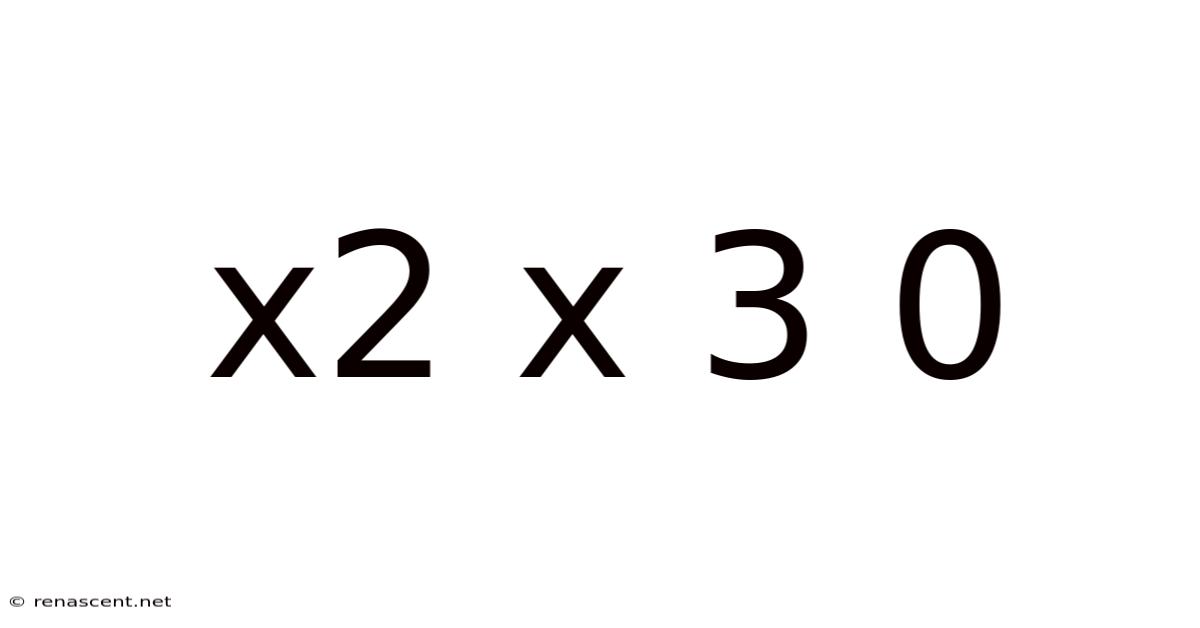
Table of Contents
Decoding "x2 x 3 0": Exploring Mathematical Concepts and Problem-Solving Strategies
The seemingly simple sequence "x2 x 3 0" can actually open the door to a fascinating exploration of various mathematical concepts and problem-solving strategies. At first glance, it looks like a simple mathematical expression, but a closer look reveals its potential for ambiguity and multiple interpretations. This article will delve into different ways to understand this sequence, exploring potential meanings, applying mathematical operations, and discussing the importance of clarity and precision in mathematical communication. We'll also tackle common questions and misconceptions associated with such ambiguous expressions.
Understanding the Ambiguity: Why "x2 x 3 0" is Not Straightforward
The primary challenge with "x2 x 3 0" lies in its lack of explicit operators and the inherent ambiguity of the "x". Is "x" a variable representing an unknown number? Is it a multiplication sign? Or is it something else entirely? Without further context or clarification, multiple interpretations are possible. This highlights the crucial role of precise mathematical notation in avoiding confusion. A poorly defined expression can lead to incorrect calculations and flawed conclusions.
Possible Interpretations and Solutions
Let's explore some plausible interpretations of "x2 x 3 0", assuming "x" represents multiplication:
Interpretation 1: Sequential Multiplication
This interpretation assumes a straightforward sequential multiplication: (2 x 3) x 0. Following the order of operations (PEMDAS/BODMAS), we first calculate 2 x 3 = 6, and then multiply the result by 0. This yields a final answer of 0. This is a simple and intuitive interpretation, but may not be the only one.
Interpretation 2: Implicit Parentheses and Variable x
Let's assume "x" is a variable. We could interpret the expression as: x * 2 * 3 = 0. In this case, we can solve for x. Dividing both sides by 6 (2 x 3), we find that x = 0. This approach introduces an algebraic element, transforming the sequence into a simple equation to be solved.
Interpretation 3: Exploring Different Base Systems
Although less likely without additional context, the sequence could be interpreted within the framework of different base systems (e.g., binary, ternary, hexadecimal). However, without specifying the base, this interpretation remains speculative and requires further information to be solved meaningfully. Consideration of different base systems highlights the importance of always clarifying the number system used in a mathematical problem.
Interpretation 4: Considering the "x" as an Unknown Operation
This interpretation explores the possibility that "x" is a placeholder for an unknown operation, not necessarily multiplication. This leads to an almost infinite number of potential interpretations, emphasizing the necessity of clearly defining the operation intended in a mathematical problem. The ambiguity is central to the problem's nature and illustrates that without further context, there's no single right solution.
Expanding on Mathematical Concepts
The seemingly simple sequence "x2 x 3 0" provides an excellent opportunity to discuss several crucial mathematical concepts:
1. Order of Operations: The sequence underscores the importance of following the order of operations (PEMDAS/BODMAS) – Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). Ignoring this order can lead to vastly different results. The correct application of order of operations ensures consistency and accuracy in mathematical calculations.
2. Variables and Equations: Interpreting "x" as a variable transforms the sequence into an algebraic equation that can be solved for the unknown value. This introduces a foundational element of algebra – solving for unknowns through manipulation of equations. This showcases the transition from arithmetic to algebra, a crucial step in advanced mathematical studies.
3. Number Systems: The possibility of interpreting the sequence within different number systems highlights the concept of representing numbers in various bases. Understanding binary, ternary, or hexadecimal systems broadens mathematical understanding and demonstrates the flexibility of numerical representation.
4. Mathematical Notation and Communication: The ambiguity of "x2 x 3 0" underscores the critical importance of clear and unambiguous mathematical notation. Precise use of symbols, operators, and parentheses is essential for effective communication and prevents errors arising from misinterpretations. This emphasizes the need for proper communication in mathematics for avoiding any misinterpretations.
Problem-Solving Strategies
Solving problems with ambiguous expressions requires a systematic approach:
1. Clarify Assumptions: Before attempting a solution, explicitly state any assumptions made about the meaning of symbols and operations. This transparency ensures that the solution's reasoning is clear and understandable.
2. Explore Multiple Interpretations: Consider all plausible interpretations of the expression, recognizing that multiple valid solutions might exist depending on the assumptions made.
3. Apply Mathematical Principles: Employ relevant mathematical principles, such as order of operations and algebraic manipulations, to solve the expression under each interpretation.
4. Evaluate Results: After obtaining a solution for each interpretation, analyze the results and critically evaluate their validity within the context of the problem.
5. Communicate Clearly: Document your approach clearly, outlining the assumptions, methods, and reasoning used to arrive at each solution. This ensures clarity and allows others to understand the solution process, facilitating collaboration and reducing errors.
Frequently Asked Questions (FAQ)
Q: What is the "correct" answer to x2 x 3 0?
A: There isn't a single "correct" answer without further clarification. The ambiguity in the expression allows for multiple valid solutions, depending on how "x" and the sequence of operations are interpreted.
Q: Why is precise mathematical notation important?
A: Precise notation minimizes ambiguity and ensures that mathematical expressions are interpreted consistently by everyone. It's essential for accurate calculations and clear communication.
Q: How can I avoid similar ambiguities in my own mathematical work?
A: Always use parentheses to clarify the order of operations, clearly define variables, and specify the number system being used. Avoid ambiguous symbols or notation whenever possible.
Conclusion: The Value of Ambiguity in Learning
While the ambiguity of "x2 x 3 0" might seem frustrating, it serves as a valuable learning experience. It highlights the importance of clear communication, the power of problem-solving strategies, and the exploration of multiple mathematical concepts within a seemingly simple sequence. By analyzing this expression, we've not only learned to solve mathematical expressions but also to appreciate the nuances of mathematical language and the critical thinking skills required for effective problem-solving. The lesson is clear: clarity in mathematics is paramount, and exploring ambiguity can significantly enhance our understanding of the subject. The seemingly simple sequence "x2 x 3 0" offers a rich and rewarding exploration into the depth of mathematical thinking.
Latest Posts
Latest Posts
-
8 3 Kg To Lbs
Sep 13, 2025
-
83 F In C
Sep 13, 2025
-
98 9 F To C
Sep 13, 2025
-
1 25 Liters To Kg
Sep 13, 2025
-
2 25 In To Mm
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X2 X 3 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.