0.06 As A Percentage
renascent
Sep 18, 2025 · 6 min read
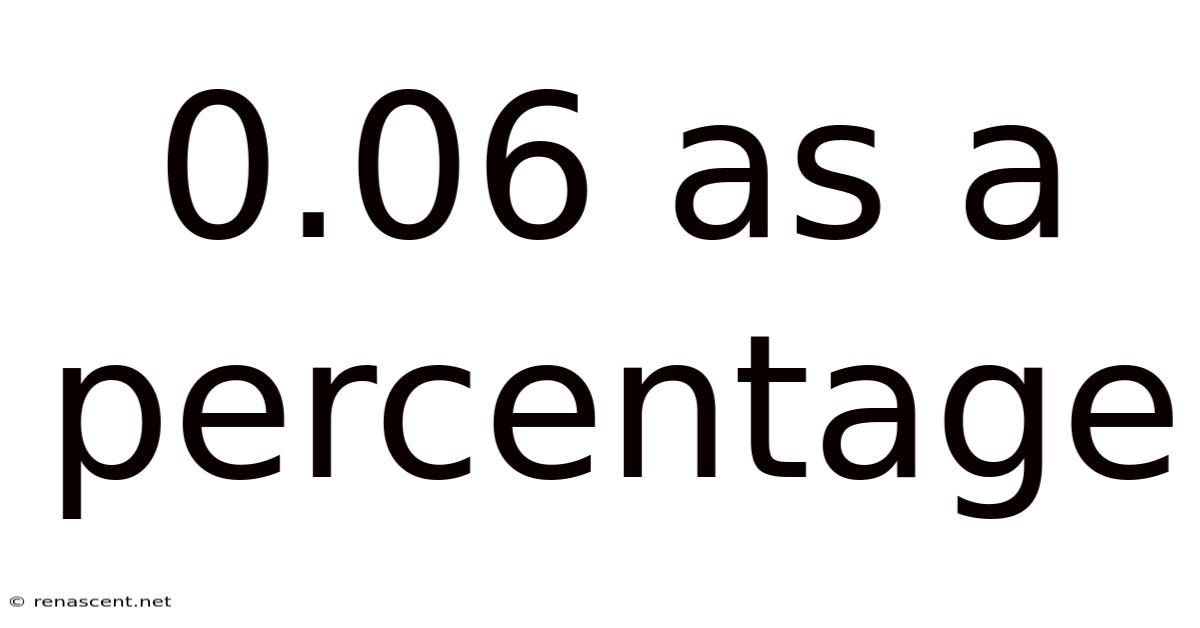
Table of Contents
Understanding 0.06 as a Percentage: A Comprehensive Guide
Understanding decimals and their conversion to percentages is a fundamental skill in mathematics and numerous real-world applications. This article provides a comprehensive guide to understanding 0.06 as a percentage, exploring its meaning, calculation methods, real-world examples, and addressing frequently asked questions. Whether you're a student struggling with decimal-to-percentage conversions, a professional needing a quick refresher, or simply curious about the topic, this guide will equip you with the knowledge and confidence to confidently work with percentages and decimals.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." We use the symbol "%" to represent percentages. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively in various fields, including finance, statistics, and everyday life, to represent proportions, rates, and changes.
Converting Decimals to Percentages
To convert a decimal to a percentage, you simply multiply the decimal by 100 and add the percent symbol (%). This is because percentages are based on a scale of 100. The formula is:
Percentage = Decimal × 100%
Let's apply this to our example, 0.06:
Percentage = 0.06 × 100% = 6%
Therefore, 0.06 is equivalent to 6%.
Understanding 0.06 as a Percentage in Different Contexts
The meaning of 0.06 as a percentage (6%) varies depending on the context. Let's explore some examples:
-
Financial Context: If a company reports a 6% growth in profit, it means that its profit increased by 6 units for every 100 units of profit in the previous period. This could indicate a relatively small but positive growth. Conversely, a 6% decrease in sales would imply a reduction of 6 units for every 100 units sold previously.
-
Statistical Context: In statistical analysis, 6% could represent the percentage of a population with a particular characteristic or the percentage of successful outcomes in an experiment. For instance, if 6% of a sample of 1000 people prefer a particular brand of coffee, it means 60 people (6% of 1000) in the sample prefer that brand.
-
Rate of Return: If an investment yields a 6% return, it means that for every $100 invested, you would gain an additional $6. This is a common way to express investment performance.
-
Discount: A 6% discount on an item means you save $6 for every $100 of the original price.
-
Tax Rate: A 6% sales tax means that for every $100 you spend, you'll pay an additional $6 in taxes.
These examples highlight the versatility of percentages in representing proportions and changes in various situations. Understanding the context is crucial for accurate interpretation.
Different Ways to Express 0.06
It's important to understand that 0.06 can be expressed in multiple ways, all representing the same value:
- Decimal: 0.06
- Percentage: 6%
- Fraction: 6/100 (which can be simplified to 3/50)
Being able to switch between these representations is essential for solving various mathematical problems and understanding different types of data.
Working with Percentages and Decimals: Advanced Applications
Beyond the simple conversion, working with percentages and decimals often involves more complex calculations. Let's explore some scenarios:
1. Calculating a Percentage of a Number:
To find 6% of a number, say 200, you multiply the number by the decimal equivalent of the percentage:
200 × 0.06 = 12
Therefore, 6% of 200 is 12.
2. Finding the Original Amount After a Percentage Change:
If a quantity increased by 6% to reach a new value, you can find the original amount using the following formula:
Original Amount = New Amount / (1 + Percentage Increase as a Decimal)
For example, if a quantity increased by 6% to become 212, the original amount is:
Original Amount = 212 / (1 + 0.06) = 212 / 1.06 ≈ 200
3. Calculating Percentage Change:
To calculate the percentage change between two numbers, use the following formula:
Percentage Change = [(New Value - Old Value) / Old Value] × 100%
For example, if a value increased from 200 to 212, the percentage change is:
Percentage Change = [(212 - 200) / 200] × 100% = 6%
Real-World Examples of 0.06 (6%)
The application of 0.06 as a percentage extends far beyond textbook examples. Here are some real-world scenarios:
-
Interest Rates: Savings accounts, loans, and credit cards often have interest rates expressed as percentages. A 6% interest rate on a loan means you pay 6% of the loan amount as interest annually.
-
Inflation: Inflation rates represent the percentage increase in the general price level of goods and services. A 6% inflation rate means the cost of goods and services has increased by 6%.
-
Stock Market Returns: Stock market investments can experience both gains and losses. A 6% return on investment signifies a positive growth, whereas a 6% loss indicates a decline in the investment's value.
-
Sales Tax: Sales tax is a percentage of the price of goods and services, added to the final amount. A 6% sales tax means you pay 6% of the pre-tax cost as tax.
Frequently Asked Questions (FAQ)
Q1: How do I convert a fraction to a percentage?
To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100%. For example, to convert 3/50 to a percentage: (3/50) × 100% = 6%
Q2: What if I have a negative decimal? How do I convert it to a percentage?
Follow the same procedure as with positive decimals: multiply the negative decimal by 100% and add the percent symbol. For example, -0.06 becomes -6%.
Q3: Can percentages be greater than 100%?
Yes, percentages can be greater than 100%. This indicates that a value has increased by more than its original value. For example, if a quantity doubles, it represents a 200% increase.
Q4: How can I use percentages to compare different quantities?
Percentages are excellent for comparing quantities of different sizes. By expressing them as percentages, you can easily compare proportions and make meaningful comparisons.
Q5: Are there any online tools to help with percentage calculations?
Numerous online calculators and converters are readily available to assist with percentage calculations, decimal-to-percentage conversions, and other related mathematical operations.
Conclusion
Understanding 0.06 as a percentage (6%) is a fundamental skill with wide-ranging applications. This article has covered the basics of percentage calculations, illustrated the versatility of 0.06 in various contexts, and explored advanced applications. Mastering decimal-to-percentage conversions and understanding the underlying concepts is essential for success in various academic and professional settings. Remember, practice is key – the more you work with percentages and decimals, the more comfortable and confident you'll become. By understanding the principles outlined in this guide, you can approach percentage-related problems with increased confidence and accuracy. From analyzing financial reports to interpreting statistical data, the ability to work confidently with percentages is a valuable skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
Great Movie Music Composers
Sep 18, 2025
-
420 Divided By 10
Sep 18, 2025
-
Kpa To Kn M2
Sep 18, 2025
-
1000 Microliter To Ml
Sep 18, 2025
-
South America Electrical Plugs
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 0.06 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.