0.6 Divided By 4
renascent
Sep 14, 2025 · 6 min read
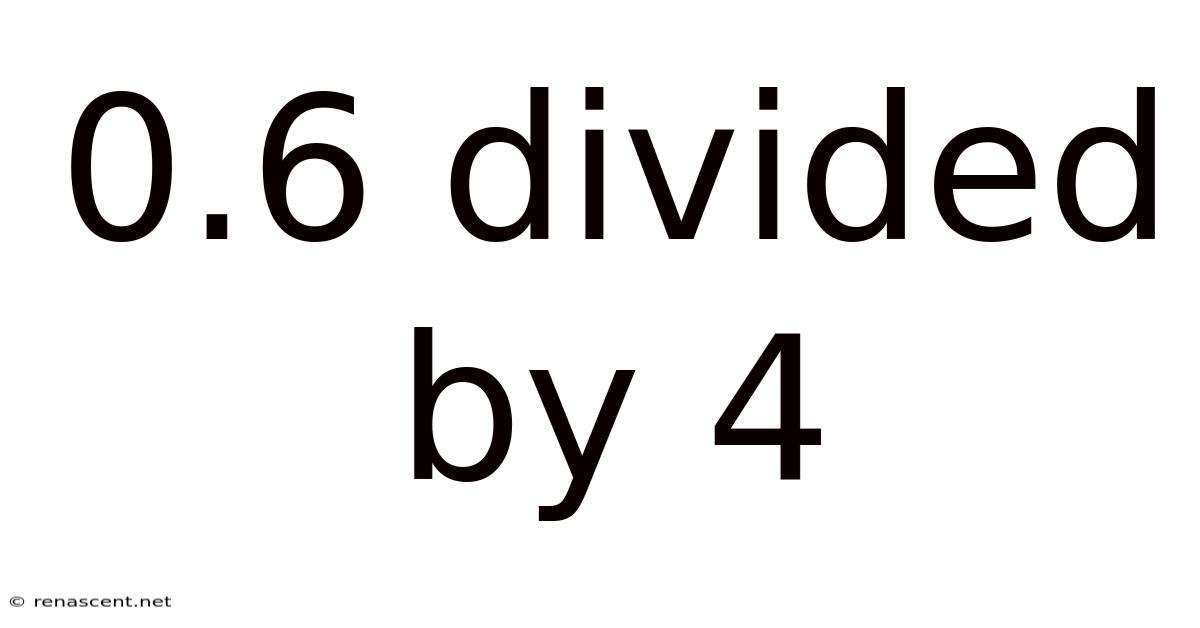
Table of Contents
Unveiling the Mystery: A Deep Dive into 0.6 Divided by 4
Dividing decimals can seem daunting, especially when you're dealing with numbers like 0.6 divided by 4. This seemingly simple calculation actually provides a great opportunity to explore fundamental mathematical concepts and build a strong understanding of decimal division. This article will guide you through the process, explaining not just how to get the answer but why the method works, covering various approaches and addressing common misconceptions. We'll explore different methods, from the traditional long division to utilizing fractions, ensuring a comprehensive understanding for all levels.
Understanding the Problem: 0.6 ÷ 4
Before jumping into the calculations, let's clarify what the problem 0.6 ÷ 4 actually means. It asks: "If we divide the quantity 0.6 into 4 equal parts, how large is each part?" This phrasing helps visualize the problem and connects the abstract concept of division to a tangible scenario. Understanding this context makes the process more intuitive and less intimidating.
Method 1: Long Division – The Classic Approach
The traditional long division method provides a systematic way to solve this problem. Here's a step-by-step guide:
-
Set up the problem: Write the problem as a long division problem: 4 | 0.6
-
Add a decimal point: Since we're dividing a decimal, add a decimal point directly above the decimal point in the dividend (0.6). This ensures proper placement of the decimal point in the quotient.
-
Add zeros: Add a zero to the dividend (0.6 becomes 0.60). This allows for continued division even if the dividend is smaller than the divisor. You can add as many zeros as needed.
-
Divide: Now, divide 4 into 0.6. Since 4 doesn't go into 0, move to the next digit (6). 4 goes into 6 once (4 x 1 = 4). Write "1" above the 6 in the quotient.
-
Subtract: Subtract 4 from 6 (6 - 4 = 2).
-
Bring down the next digit: Bring down the next digit (0) from the dividend. This gives you 20.
-
Divide again: Now, divide 4 into 20. 4 goes into 20 five times (4 x 5 = 20). Write "5" above the 0 in the quotient.
-
Subtract: Subtract 20 from 20 (20 - 20 = 0). Since there's no remainder, the division is complete.
Therefore, 0.6 ÷ 4 = 0.15
Method 2: Converting to Fractions – A Different Perspective
Fractions offer an alternative approach to solving decimal division problems. Here’s how to solve 0.6 ÷ 4 using fractions:
-
Convert the decimal to a fraction: The decimal 0.6 can be written as the fraction 6/10.
-
Rewrite the division problem: The problem 0.6 ÷ 4 becomes (6/10) ÷ 4.
-
Rewrite the division as a multiplication: Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of 4 is 1/4. So, (6/10) ÷ 4 is equivalent to (6/10) x (1/4).
-
Multiply the numerators and denominators: Multiply the numerators (6 x 1 = 6) and the denominators (10 x 4 = 40). This gives you 6/40.
-
Simplify the fraction: Both the numerator (6) and denominator (40) are divisible by 2. Simplifying, we get 3/20.
-
Convert the fraction back to a decimal: To convert 3/20 to a decimal, divide the numerator (3) by the denominator (20). This gives you 0.15.
Method 3: Using Decimal Multiplication – A Shortcut
This method utilizes the knowledge that division is the inverse operation of multiplication. We can essentially ask: "What number, when multiplied by 4, equals 0.6?" This approach involves a little trial and error or estimation:
- We know 4 x 0.1 = 0.4
- 4 x 0.2 = 0.8
Since 0.6 lies between 0.4 and 0.8, the answer will be between 0.1 and 0.2. We can further refine our estimation. By dividing 0.6 by 4 using any of the previous methods we arrive at 0.15.
Understanding the Result: The Significance of 0.15
The answer, 0.15, represents one-fourth of 0.6. Imagine a pizza sliced into ten equal pieces. You have six slices (0.6 of the pizza). If you divide these six slices into four equal groups, each group will consist of 1.5 slices, which is equivalent to 1.5/10 or 0.15 of the whole pizza. This illustrates the practical application of decimal division.
Common Mistakes and How to Avoid Them
Several common errors can occur when dividing decimals:
-
Incorrect decimal placement: The most frequent mistake is misplacing the decimal point in the quotient. Carefully aligning the decimal point in the dividend and the quotient is crucial.
-
Errors in subtraction: Accuracy in subtraction is vital. Any mistake in the subtraction steps will lead to an incorrect answer. Double-check your subtractions.
-
Forgetting to add zeros: When the divisor doesn't go into the dividend evenly, remember to add zeros to continue the division process. This ensures that you get the most accurate answer.
-
Incorrect simplification of fractions: If using the fraction method, ensure you simplify the fraction to its lowest terms before converting it back to a decimal.
Further Exploration: Extending the Concept
Understanding 0.6 ÷ 4 lays a strong foundation for tackling more complex decimal division problems. By grasping the fundamental principles, you can confidently solve problems involving larger numbers, multiple decimal places, and even division by decimals themselves.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve 0.6 ÷ 4? A: Yes, calculators provide a quick and efficient way to solve decimal division problems. However, understanding the underlying mathematical principles remains important for building a strong foundation in mathematics.
-
Q: What if the division doesn't result in a whole number? A: Many decimal division problems result in decimals, not whole numbers. The process remains the same; you'll simply have a decimal in your answer.
-
Q: What happens if the divisor is a decimal number? A: Dividing by a decimal involves an additional step: converting the divisor into a whole number by multiplying both the divisor and dividend by a power of 10. This ensures easier and more accurate division.
-
Q: Are there other ways to represent the answer 0.15? A: Yes, 0.15 can also be represented as a fraction (3/20) or as a percentage (15%).
Conclusion: Mastering Decimal Division
0.6 divided by 4, seemingly a simple problem, offers a rich learning opportunity. By exploring different methods and understanding the rationale behind each step, you build a strong understanding of decimal division and develop crucial mathematical skills. Remember the importance of accurate decimal placement, meticulous subtraction, and thoughtful simplification. The ability to solve this type of problem effectively translates to broader mathematical competency and problem-solving skills. The journey of understanding this seemingly simple calculation opens doors to more complex mathematical concepts, fostering a deeper appreciation for the beauty and logic of numbers. Keep practicing, and you'll master decimal division in no time!
Latest Posts
Latest Posts
-
157 Pounds To Kg
Sep 14, 2025
-
88 Divided By 4
Sep 14, 2025
-
58 25 Kg To Lbs
Sep 14, 2025
-
Differentiate Religion From Spirituality
Sep 14, 2025
-
36 3 C To F
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 0.6 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.