88 Divided By 4
renascent
Sep 14, 2025 · 6 min read
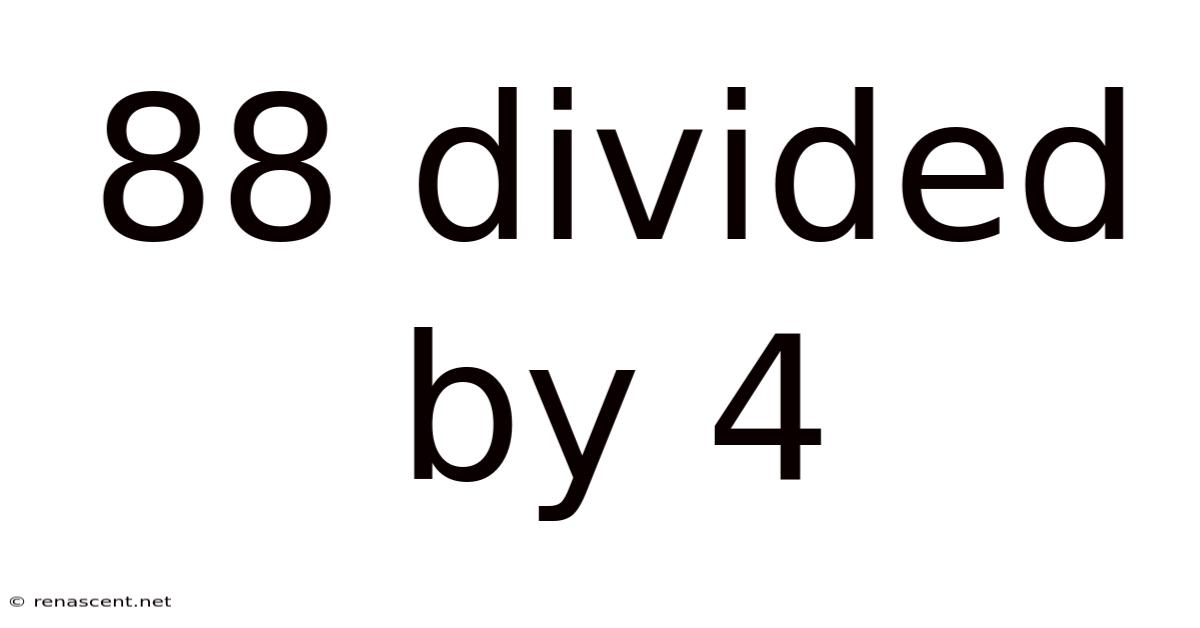
Table of Contents
Unpacking 88 Divided by 4: A Deep Dive into Division
Dividing 88 by 4 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation opens doors to a broader understanding of division, its applications in various fields, and its connection to other mathematical concepts. This article will delve into the process of solving 88 ÷ 4, exploring different methods, demonstrating its practical uses, and addressing common misconceptions. We'll go beyond the simple answer and explore the underlying principles, making this a comprehensive guide for anyone wanting a deeper understanding of division.
Understanding the Basics of Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It's essentially the process of splitting a quantity into equal parts. In the context of 88 ÷ 4, we're asking: "How many times does 4 fit into 88?" The answer, as we will see, represents the size of each equal group when 88 is divided into 4 groups. This concept is crucial, regardless of the numbers involved.
Method 1: Long Division
The traditional method for solving 88 ÷ 4 is long division. This method, while potentially time-consuming for larger numbers, offers a systematic approach that helps build a solid understanding of the division process. Here's how it works:
-
Set up the problem: Write the dividend (88) inside the long division symbol (⟌) and the divisor (4) outside.
4⟌88 -
Divide the tens digit: The first step involves dividing the tens digit of the dividend (8) by the divisor (4). 8 ÷ 4 = 2. Write the quotient (2) above the tens digit of the dividend.
2 4⟌88 -
Multiply and subtract: Multiply the quotient (2) by the divisor (4), resulting in 8. Subtract this result from the tens digit of the dividend (8 - 8 = 0).
2 4⟌88 -8 -- 0 -
Bring down the ones digit: Bring down the ones digit of the dividend (8) next to the remainder (0).
2 4⟌88 -8 -- 08 -
Divide the ones digit: Divide the new number (8) by the divisor (4). 8 ÷ 4 = 2. Write this quotient (2) above the ones digit of the dividend.
22 4⟌88 -8 -- 08 -8 -- 0 -
Multiply and subtract: Multiply the new quotient (2) by the divisor (4), resulting in 8. Subtract this from the remaining number (8 - 8 = 0). The remainder is 0.
Therefore, 88 ÷ 4 = 22.
Method 2: Repeated Subtraction
This method is excellent for visualizing the division process. It involves repeatedly subtracting the divisor (4) from the dividend (88) until the result is 0 or less than the divisor. The number of times you subtract is the quotient.
- Start with 88.
- Subtract 4: 88 - 4 = 84
- Subtract 4: 84 - 4 = 80
- Continue subtracting 4 until you reach 0. You'll find you've subtracted 4 a total of 22 times.
Therefore, 88 ÷ 4 = 22. This method highlights the concept of division as repeated subtraction.
Method 3: Using Multiplication
Division and multiplication are inverse operations. This means that if you know the multiplication facts, you can easily find the answer to a division problem. Since 4 x 20 = 80, and 4 x 2 = 8, we can deduce that 4 x 22 = 88. Therefore, 88 ÷ 4 = 22. This method works best when you're familiar with your multiplication tables.
Real-World Applications of Division: Examples Using 88 ÷ 4
The seemingly simple calculation of 88 ÷ 4 has numerous practical applications in everyday life:
-
Sharing Equally: Imagine you have 88 candies and want to share them equally among 4 friends. Using 88 ÷ 4, you'd find each friend receives 22 candies.
-
Unit Pricing: If a pack of 4 pencils costs $88, the price per pencil is $88 ÷ 4 = $22.
-
Distance Calculation: If a car travels 88 miles in 4 hours at a constant speed, its average speed is 88 miles ÷ 4 hours = 22 miles per hour.
-
Recipe Scaling: A recipe calls for 88 grams of flour, but you only want to make a quarter of the recipe. You would need 88 grams ÷ 4 = 22 grams of flour.
-
Average Calculation: Suppose you have four test scores that add up to 88. Your average score would be 88 ÷ 4 = 22.
Understanding Remainders
While 88 ÷ 4 results in a whole number (22), division problems don't always have a zero remainder. For example, if we divide 89 by 4, we get 22 with a remainder of 1 (22 R1). The remainder represents the amount left over after the division is complete. Understanding remainders is crucial in various contexts, such as determining the number of buses needed to transport a group of students or calculating the number of complete sets from a given quantity.
Connecting Division to Other Mathematical Concepts
Division is deeply intertwined with other mathematical concepts:
-
Fractions: The division problem 88 ÷ 4 can be represented as the fraction 88/4. Simplifying this fraction gives us 22/1, or simply 22.
-
Decimals: If we were dividing a number that didn't divide evenly, we'd obtain a decimal answer. For example, 89 divided by 4 is 22.25.
-
Algebra: Division is a fundamental operation in algebraic equations. Solving equations often involves isolating a variable by dividing both sides of the equation by a certain value.
Common Misconceptions About Division
-
Order of Operations: Division must follow the order of operations (PEMDAS/BODMAS). This means division is performed after parentheses/brackets, exponents/orders, and multiplication, but before addition and subtraction.
-
Dividing by Zero: Dividing any number by zero is undefined. This is a fundamental rule in mathematics.
-
Confusing Dividend and Divisor: Remember the dividend is the number being divided, and the divisor is the number by which we divide.
Frequently Asked Questions (FAQ)
-
Q: What is the inverse operation of division?
- A: Multiplication.
-
Q: Can you divide by a fraction?
- A: Yes, dividing by a fraction is the same as multiplying by its reciprocal.
-
Q: What is the difference between division and subtraction?
- A: Subtraction involves removing a quantity from another quantity, while division involves splitting a quantity into equal parts.
-
Q: How can I improve my division skills?
- A: Practice regularly using different methods, work through problems with varying difficulty, and use visual aids if needed.
Conclusion
This in-depth exploration of 88 divided by 4 has revealed more than just the simple answer of 22. We've uncovered the fundamental principles of division, explored various methods for solving division problems, highlighted practical applications, and addressed common misconceptions. Understanding division goes beyond simply obtaining the answer; it's about comprehending the underlying concepts and appreciating its crucial role in various mathematical and real-world scenarios. By understanding the process and its connections to other mathematical concepts, we develop a more robust and versatile mathematical foundation. This detailed analysis serves as a stepping stone to tackling more complex division problems and furthering mathematical understanding. The seemingly simple calculation of 88 ÷ 4 opens a gateway to a much broader and more enriching understanding of mathematics.
Latest Posts
Latest Posts
-
10 Percent Of 300
Sep 14, 2025
-
25 Percent Of 500
Sep 14, 2025
-
Crown Tattoos For Guys
Sep 14, 2025
-
Whats 2 Of 3000
Sep 14, 2025
-
230 Kph To Mph
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 88 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.