0.8 As A Percent
renascent
Sep 20, 2025 · 5 min read
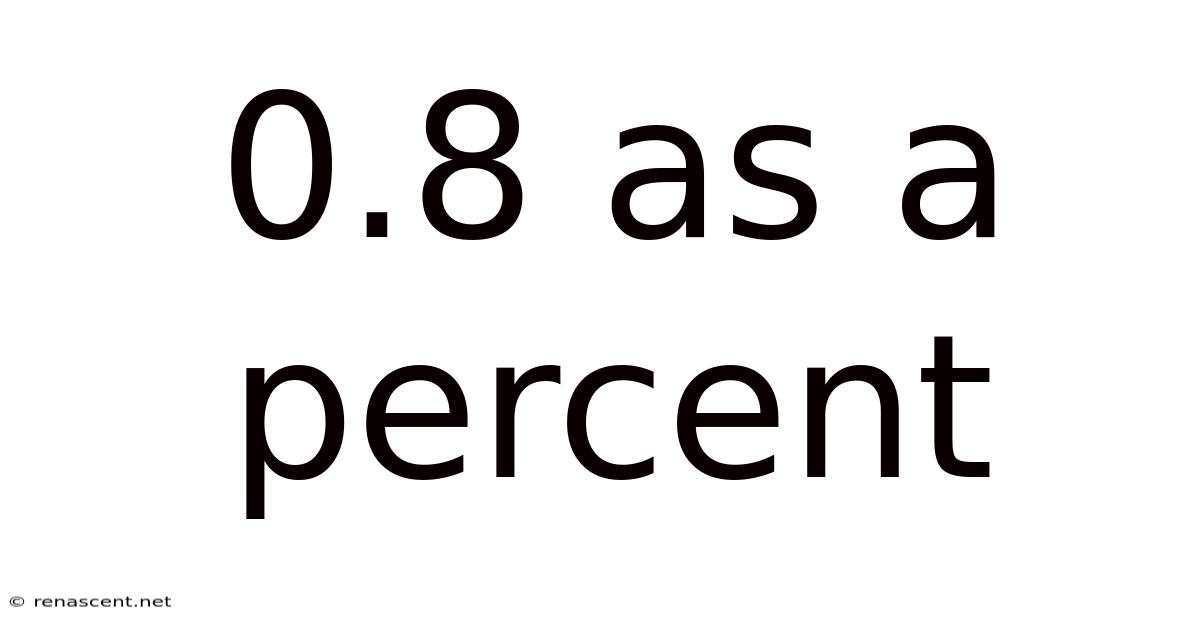
Table of Contents
Understanding 0.8 as a Percent: A Comprehensive Guide
Decimals and percentages are fundamental concepts in mathematics, frequently encountered in various aspects of life, from calculating discounts in a shop to understanding financial reports. This comprehensive guide will delve into the meaning of 0.8 as a percentage, exploring its conversion, applications, and practical implications. We'll cover everything from the basic principles to more advanced applications, ensuring a thorough understanding for all readers.
Introduction: Decimals, Percentages, and the Conversion Process
Before we tackle 0.8 specifically, let's review the core relationship between decimals and percentages. A percentage represents a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). Converting between decimals and percentages involves a simple manipulation of these fractional representations.
To convert a decimal to a percentage, you multiply the decimal by 100 and add the "%" symbol. Conversely, to convert a percentage to a decimal, you divide the percentage by 100 and remove the "%" symbol. This fundamental understanding is crucial for tackling the conversion of 0.8 to a percentage.
Converting 0.8 to a Percentage
Now, let's focus on the specific decimal 0.8. Following the conversion rule, we multiply 0.8 by 100:
0.8 * 100 = 80
Therefore, 0.8 is equal to 80%. This simple calculation reveals that 0.8 represents eighty out of one hundred parts of a whole.
Visualizing 0.8 as a Percentage
Understanding percentages can be easier when visualized. Imagine a 100-square grid. If you shade 80 of those squares, you've visually represented 80%, which is equivalent to the decimal 0.8. This visual representation helps solidify the concept of 0.8 representing a significant portion – almost four-fifths – of a whole.
Applications of 0.8 (or 80%) in Real-World Scenarios
The representation of 0.8 as 80% has numerous practical applications across various fields:
-
Finance: Imagine a bank offering an 80% loan-to-value ratio (LTV) on a mortgage. This means the bank will lend you 80% of your property's value. Understanding this percentage is crucial for determining your down payment and overall financial commitment.
-
Statistics and Probability: In statistical analysis, 0.8 or 80% might represent the probability of a certain event occurring. For instance, a weather forecast might predict an 80% chance of rain. This indicates a high likelihood of rain, helping individuals make informed decisions.
-
Academic Performance: In some grading systems, a score of 0.8 or 80% might represent a high B or a low A grade. This understanding is vital for students to track their academic progress and identify areas for improvement.
-
Sales and Discounts: A store might offer an 80% discount on certain items. Knowing that 0.8 represents 80% allows you to quickly calculate the final price after the discount is applied. For example, an item initially priced at $100 would cost $20 after an 80% discount ($100 - ($100 * 0.8) = $20).
-
Project Management: In project management, 0.8 or 80% might represent the completion percentage of a project. Tracking project completion in percentages provides a clear visual representation of progress.
Understanding Fractions and Their Relation to Decimals and Percentages
It's essential to understand the interconnectedness of fractions, decimals, and percentages. 0.8 can also be expressed as a fraction: 8/10, which can be simplified to 4/5. This fractional representation reinforces the idea that 0.8 represents four-fifths of a whole. The ability to seamlessly move between these three representations is crucial for efficient mathematical problem-solving.
Advanced Applications: Compounding and Growth
The concept of 0.8 (or 80%) extends beyond simple calculations. In scenarios involving compounding or growth, understanding this percentage becomes more critical. For instance, if a population grows by 80% annually, it's essential to understand how this repeated growth affects the final population size after several years. This involves applying the concept of exponential growth, which requires a more in-depth mathematical understanding.
Solving Problems Involving 0.8 (80%)
Let's explore some example problems to further illustrate the practical application of 0.8 as a percentage:
Problem 1: A retailer offers an 80% discount on a product originally priced at $50. What is the final price of the product?
Solution:
- Calculate the discount amount: $50 * 0.8 = $40
- Subtract the discount from the original price: $50 - $40 = $10
- The final price of the product is $10.
Problem 2: A student scored 80% on a test with 50 questions. How many questions did the student answer correctly?
Solution:
- Convert the percentage to a decimal: 80% = 0.8
- Multiply the number of questions by the decimal: 50 * 0.8 = 40
- The student answered 40 questions correctly.
Problem 3: A company's profits increased by 80% this year compared to last year. If last year's profit was $100,000, what is this year's profit?
Solution:
- Calculate the increase in profit: $100,000 * 0.8 = $80,000
- Add the increase to last year's profit: $100,000 + $80,000 = $180,000
- This year's profit is $180,000.
Frequently Asked Questions (FAQs)
Q1: Is 0.8 the same as 8%?
A1: No, 0.8 is equal to 80%, not 8%. Remember, to convert a decimal to a percentage, you multiply by 100.
Q2: How can I convert 80% back to a decimal?
A2: To convert 80% back to a decimal, divide by 100: 80 / 100 = 0.8
Q3: What are some other ways to represent 0.8?
A3: Besides 80% and 4/5, 0.8 can also be expressed as 8/10 or other equivalent fractions.
Q4: What if I need to calculate a percentage that isn't a whole number?
A4: The same principles apply. For example, to calculate 25.5% of a number, you would convert 25.5% to the decimal 0.255 and then multiply by the number.
Conclusion: Mastering the Concept of 0.8 as a Percentage
Understanding the representation and application of 0.8 as 80% is fundamental for success in various fields. This guide has explored the conversion process, provided real-world examples, and addressed frequently asked questions. By mastering these concepts, you'll be equipped to confidently tackle a wide range of problems involving percentages, decimals, and fractions, enhancing your mathematical skills and problem-solving abilities in various contexts. Remember that consistent practice and application are key to solidifying your understanding. Don't hesitate to revisit these concepts and try out different problems to reinforce your learning. The ability to comfortably work with percentages and decimals will prove invaluable in your academic, professional, and personal life.
Latest Posts
Latest Posts
-
Beverage Holder For Car
Sep 20, 2025
-
325 Kpa To Psi
Sep 20, 2025
-
18 Percent Of 120
Sep 20, 2025
-
Pink And Purple Mixed
Sep 20, 2025
-
Schrodinger Equation Time Dependent
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 0.8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.