18 Percent Of 120
renascent
Sep 20, 2025 · 5 min read
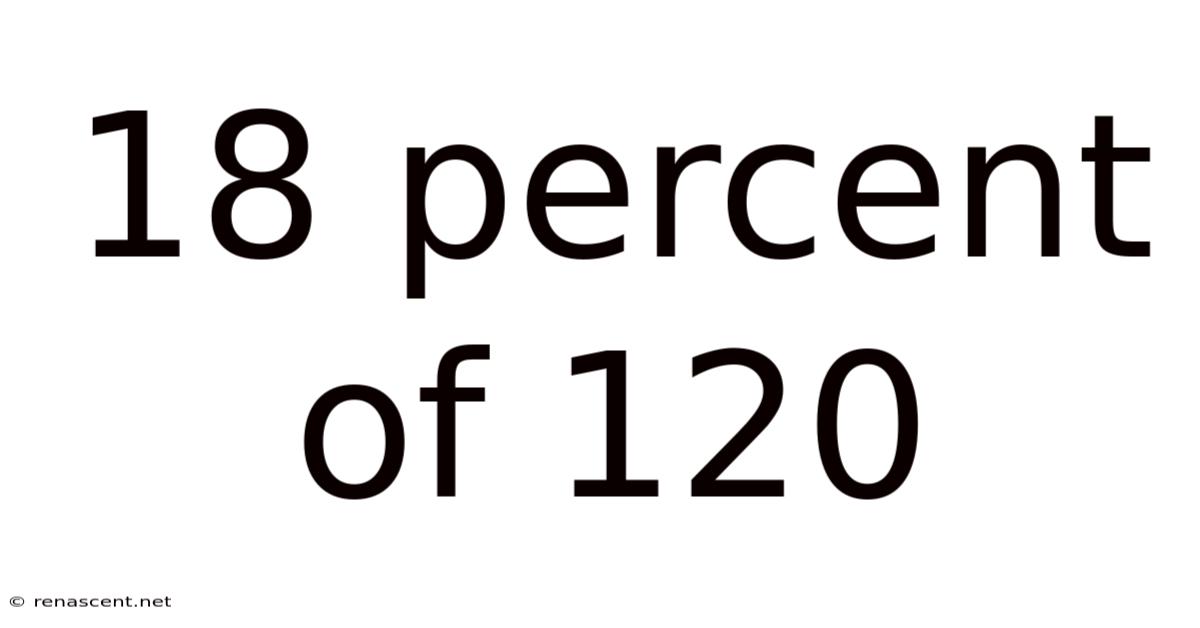
Table of Contents
Unveiling the Mystery: Calculating 18% of 120 and Mastering Percentage Calculations
Finding 18% of 120 might seem like a simple arithmetic problem, but it opens a door to understanding a fundamental concept in mathematics: percentages. This seemingly small calculation has far-reaching applications in various fields, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide will not only show you how to calculate 18% of 120 using different methods but also delve deeper into the underlying principles of percentage calculations, equipping you with the skills to tackle any percentage problem with confidence.
Understanding Percentages: A Foundation for Calculation
Before we jump into calculating 18% of 120, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this fundamental relationship between percentages, fractions, and decimals is key to mastering percentage calculations.
Method 1: Using the Basic Percentage Formula
The most straightforward method to calculate 18% of 120 is to use the basic percentage formula:
Percentage × Whole Number = Result
In this case:
- Percentage: 18% (which we need to convert to a decimal by dividing by 100: 18/100 = 0.18)
- Whole Number: 120
Therefore, the calculation becomes:
0.18 × 120 = 21.6
Therefore, 18% of 120 is 21.6.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 18% can be written as 18/100. To calculate 18% of 120 using fractions, we perform the following calculation:
(18/100) × 120
This can be simplified:
(18 × 120) / 100 = 2160 / 100 = 21.6
Again, we arrive at the answer: 18% of 120 is 21.6.
Method 3: Breaking Down the Calculation
For a deeper understanding, let's break down the calculation into smaller, manageable steps. We can calculate 10% of 120 first, and then use that result to find 18%.
- 10% of 120: (10/100) × 120 = 12
- 1% of 120: (1/100) × 120 = 1.2
- 8% of 120: 8 × 1.2 = 9.6
Now, add the results together:
12 (10%) + 9.6 (8%) = 21.6
This method helps illustrate the proportional relationship between percentages and the whole number. It's particularly useful for mental calculations or estimations.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations is crucial in various real-world scenarios:
-
Retail and Sales: Calculating discounts, sales tax, and profit margins are all based on percentages. For example, a 20% discount on a $100 item means you save $20.
-
Finance: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is vital for making informed financial decisions.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions and trends in data. For instance, the unemployment rate is expressed as a percentage of the workforce.
-
Science and Engineering: Percentages are essential in various scientific calculations, such as determining the concentration of solutions or the efficiency of processes.
Beyond the Basics: Advanced Percentage Calculations
While calculating 18% of 120 is relatively simple, more complex scenarios might involve finding the percentage increase or decrease, calculating the original value given a percentage and the result, or working with compound percentages. Let's explore some of these advanced concepts.
Calculating Percentage Increase or Decrease
Percentage increase or decrease is often used to show the change in a quantity over time. The formula for percentage change is:
[(New Value - Old Value) / Old Value] × 100%
For example, if a product's price increased from $100 to $120, the percentage increase is:
[(120 - 100) / 100] × 100% = 20%
Finding the Original Value
Sometimes you know the percentage and the result, but need to find the original value. For example, if 18% of a number is 21.6, what is the original number? We can set up an equation:
0.18 × x = 21.6
To solve for x, divide both sides by 0.18:
x = 21.6 / 0.18 = 120
The original number is 120.
Working with Compound Percentages
Compound percentages involve calculating percentages of percentages. For example, if you have a 10% increase followed by a 5% increase, the overall increase is not simply 15%. Compound percentages require sequential calculations.
Frequently Asked Questions (FAQ)
-
Q: What are the different ways to calculate percentages?
- A: You can use the basic percentage formula (Percentage × Whole Number = Result), convert the percentage to a fraction, or break down the calculation into smaller steps.
-
Q: How do I convert a percentage to a decimal?
- A: Divide the percentage by 100. For example, 18% becomes 0.18.
-
Q: How do I convert a decimal to a percentage?
- A: Multiply the decimal by 100 and add the "%" symbol. For example, 0.18 becomes 18%.
-
Q: What if I need to calculate a percentage of a number that is not a whole number?
- A: The same methods apply. You'll simply be working with decimals in your calculations.
-
Q: Are there any online calculators for percentages?
- A: Yes, many online calculators are available to assist with percentage calculations. However, understanding the underlying principles is crucial for problem-solving and application in different contexts.
Conclusion: Mastering the Art of Percentage Calculations
Calculating 18% of 120 is just one example of the many practical applications of percentage calculations. By understanding the fundamental principles and various methods of calculation, you can confidently tackle a wide range of percentage problems in various fields. Whether you're shopping for a discounted item, analyzing financial data, or solving scientific equations, a strong understanding of percentages will empower you to make informed decisions and solve problems efficiently. Remember to practice regularly to solidify your understanding and build your skills. The more you practice, the easier and more intuitive percentage calculations will become. So, go forth and conquer the world of percentages!
Latest Posts
Latest Posts
-
15 Percent Off 64
Sep 20, 2025
-
172 Pounds To Kg
Sep 20, 2025
-
4 Percent Of 800
Sep 20, 2025
-
18 20 As A Percentage
Sep 20, 2025
-
25 Degrees To Kelvin
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 18 Percent Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.