1/12 In Decimal Form
renascent
Sep 20, 2025 · 6 min read
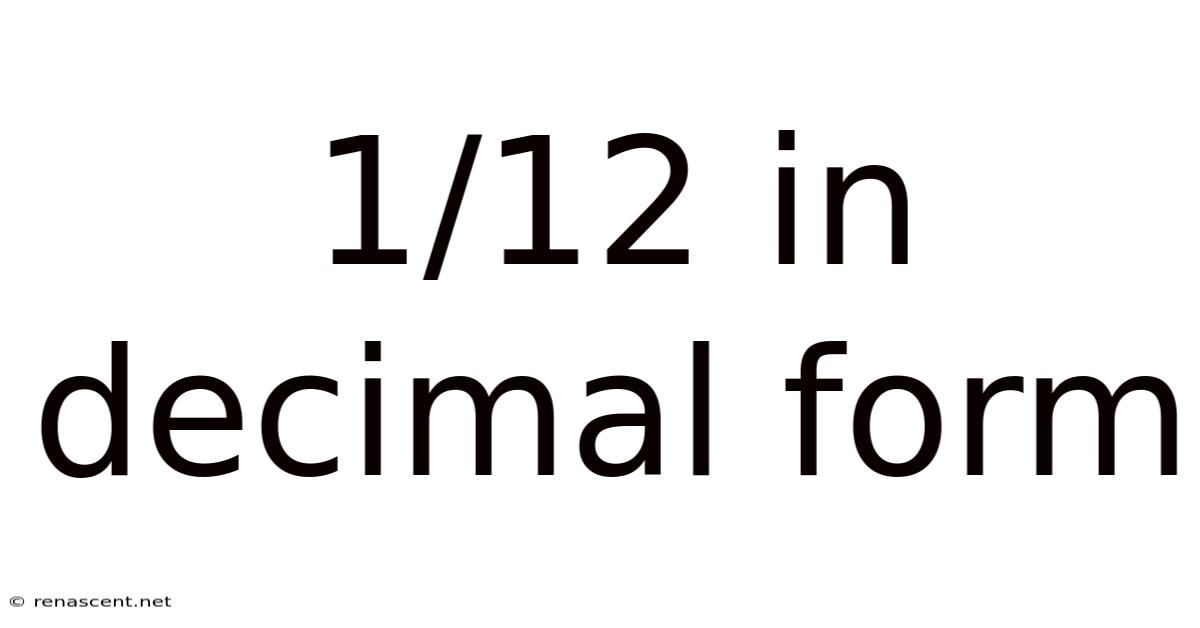
Table of Contents
Decoding 1/12: A Deep Dive into Decimal Conversions and Practical Applications
The seemingly simple fraction 1/12 might appear unremarkable at first glance. However, understanding its decimal representation and the underlying mathematical principles involved opens a door to a richer understanding of fractions, decimals, and their practical applications in various fields. This article will provide a comprehensive exploration of 1/12 in decimal form, covering its conversion process, practical applications, and frequently asked questions. We'll delve into the intricacies of decimal representation, exploring why some fractions result in terminating decimals while others, like 1/12, yield repeating decimals. By the end, you'll possess a solid grasp of this seemingly simple yet surprisingly complex topic.
Understanding Fractions and Decimals
Before diving into the specifics of 1/12, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/12, 1 is the numerator and 12 is the denominator. This indicates one out of twelve equal parts.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). Decimals are written using a decimal point (.) to separate the whole number part from the fractional part. For instance, 0.5 is equivalent to 5/10 or 1/2.
Converting a fraction to a decimal involves dividing the numerator by the denominator. This is the core process we'll use to find the decimal equivalent of 1/12.
Converting 1/12 to Decimal Form: The Long Division Method
The most straightforward method for converting 1/12 to a decimal is through long division. We divide the numerator (1) by the denominator (12):
1 ÷ 12 = ?
Performing the long division, we find that 12 does not divide evenly into 1. We add a decimal point and a zero to the dividend (1), making it 1.0. Now we can proceed with the division:
- 12 goes into 10 zero times, so we write a 0 above the decimal point.
- We bring down another zero, making it 100.
- 12 goes into 100 eight times (12 x 8 = 96). We write 8 above the second digit after the decimal point.
- We subtract 96 from 100, leaving a remainder of 4.
- We bring down another zero, making it 40.
- 12 goes into 40 three times (12 x 3 = 36). We write 3 above the third digit after the decimal point.
- We subtract 36 from 40, leaving a remainder of 4.
Notice that we've reached a remainder of 4, the same remainder we had earlier. This indicates that the division will continue indefinitely, resulting in a repeating decimal. The pattern will repeat: 0.083333...
Therefore, the decimal representation of 1/12 is 0.083̅3̅, where the bar over the 3 indicates that the digit 3 repeats infinitely.
Understanding Repeating Decimals
The result of converting 1/12 to a decimal, 0.083̅3̅, highlights an important characteristic of fractions: not all fractions can be expressed as terminating decimals (decimals that end). Some fractions, like 1/12, result in repeating decimals (decimals with a sequence of digits that repeats infinitely). This occurs when the denominator of the fraction contains prime factors other than 2 and 5 (the prime factors of 10). Since the prime factorization of 12 is 2 x 2 x 3, the presence of the 3 leads to a repeating decimal.
Contrast this with a fraction like 1/4 (which is 1/(2x2)). This fraction converts to a terminating decimal (0.25) because its denominator only contains the prime factor 2.
Practical Applications of 1/12 and Decimal Conversions
Understanding the decimal representation of 1/12, and fraction-to-decimal conversions in general, has numerous practical applications across various fields:
-
Engineering and Design: Precise measurements and calculations are crucial in engineering and design. Converting fractions to decimals allows for accurate calculations involving dimensions, angles, and other parameters. For example, in construction, a measurement of 1/12 of a foot (one inch) needs to be easily converted to its decimal equivalent for digital design tools.
-
Finance and Accounting: Working with fractions of monetary units (like calculating interest rates or distributing shares) often requires decimal conversions for accuracy and ease of calculation.
-
Science and Measurement: Scientific experiments and data analysis often involve fractions and decimals. Converting fractions to decimals facilitates calculations and data representation.
-
Computer Programming: Many programming languages require decimal representation for numerical calculations and data storage. Understanding fraction-to-decimal conversion is crucial for writing accurate and efficient code.
-
Everyday Life: Even in everyday life, converting fractions to decimals simplifies many tasks. For example, when calculating portions of recipes or sharing items among a group of people.
Advanced Concepts: Continued Fractions
For those interested in delving deeper, the concept of continued fractions provides an alternative way to represent fractions. A continued fraction expresses a fraction as a sum of fractions, where each fraction's denominator is another fraction. This representation can be particularly useful for approximations and understanding the properties of irrational numbers. While 1/12 itself doesn't exhibit particularly interesting features in its continued fraction representation, exploring this concept expands one's understanding of number systems.
Frequently Asked Questions (FAQ)
- Q: Is there another way to represent 0.083̅3̅ besides 1/12?
A: No, 0.083̅3̅ is the unique decimal representation of 1/12. Other fractions might have decimal representations that appear similar due to rounding, but 1/12 is the only fraction that produces exactly this repeating decimal.
- Q: Why does 1/12 result in a repeating decimal?
A: As mentioned earlier, the denominator 12 contains the prime factor 3, which is not a factor of 10. This leads to a repeating decimal pattern. Only fractions whose denominators are composed solely of 2s and 5s will yield terminating decimals.
- Q: How can I convert a repeating decimal back to a fraction?
A: Converting a repeating decimal back to a fraction involves algebraic manipulation. Let's illustrate with 0.083̅3̅. Let x = 0.083̅3̅. Multiplying x by 1000 gives 83.333... Subtracting 10x (0.833...) from 1000x gives 990x = 82.5. Solving for x gives x = 82.5/990 = 1/12. This method can be adapted for various repeating decimal patterns.
- Q: Are there any online tools that can convert fractions to decimals?
A: Yes, many online calculators and converters are available that can quickly and accurately convert fractions to decimals and vice-versa. These are helpful tools for checking your work or performing conversions for more complex fractions.
Conclusion
The seemingly simple fraction 1/12 reveals a rich tapestry of mathematical concepts when we explore its decimal representation. Understanding its conversion to the repeating decimal 0.083̅3̅, the reasons behind repeating decimals, and the practical applications of decimal conversions across various fields provides a solid foundation for appreciating the interconnectedness of different mathematical concepts. Whether you're an engineering student, a finance professional, or simply someone curious about numbers, mastering the art of converting fractions to decimals—and understanding the underlying principles—will prove invaluable. This detailed exploration of 1/12 should equip you with the knowledge and confidence to tackle similar conversions and enhance your understanding of the world of numbers.
Latest Posts
Latest Posts
-
18 Percent Of 120
Sep 20, 2025
-
Pink And Purple Mixed
Sep 20, 2025
-
Schrodinger Equation Time Dependent
Sep 20, 2025
-
77 Minutes In Hours
Sep 20, 2025
-
2 3 Of 288
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1/12 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.