1/2 Of 3 1/2
renascent
Sep 14, 2025 · 5 min read
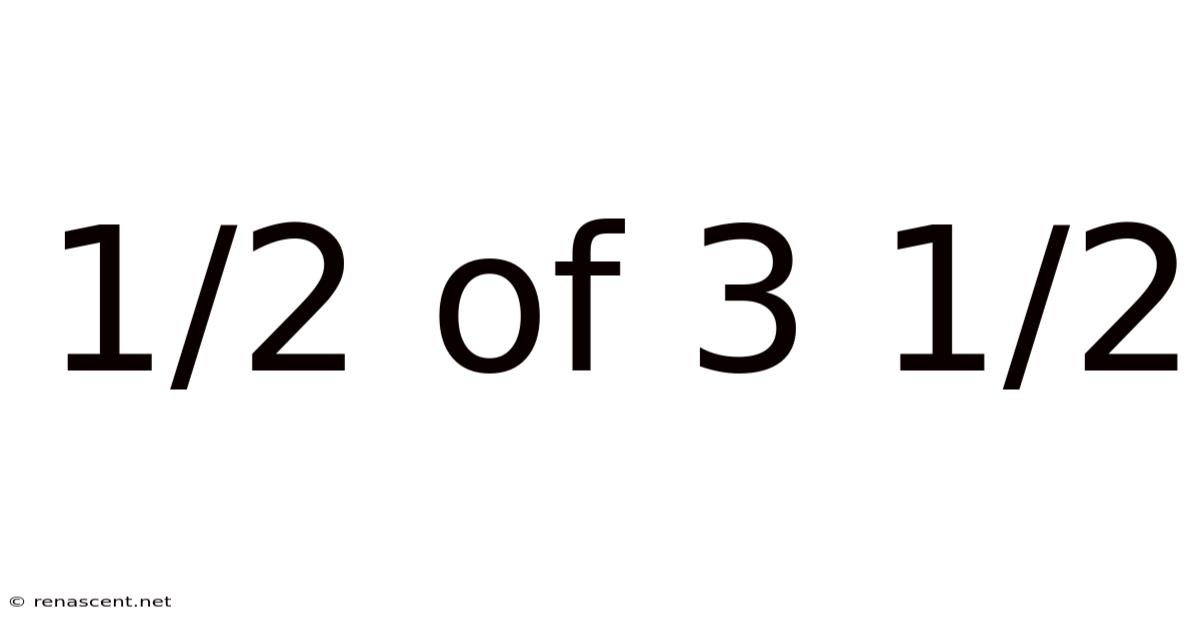
Table of Contents
Decoding the Mystery: What is 1/2 of 3 1/2? A Comprehensive Guide
This article will delve into the seemingly simple, yet often confusing, mathematical problem of calculating half of three and a half. We'll explore multiple methods to solve this, explaining the underlying principles in an accessible way, making it perfect for students, educators, or anyone looking to refresh their fractional arithmetic skills. We'll also address common misconceptions and frequently asked questions, ensuring a complete and satisfying understanding of this fundamental concept.
Introduction: Understanding Fractions and Multiplication
Before we tackle the problem of finding 1/2 of 3 1/2, let's review some key concepts. The phrase "1/2 of 3 1/2" essentially translates to finding the product of 1/2 and 3 1/2. This involves multiplying two fractions. Remember that a fraction represents a part of a whole. The number on top is called the numerator, and the number on the bottom is called the denominator. The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we are considering.
Method 1: Converting to Improper Fractions
The most straightforward method to solve this problem is by converting both mixed numbers (numbers containing both whole and fractional parts) into improper fractions. An improper fraction has a numerator larger than its denominator.
-
Step 1: Convert 3 1/2 to an improper fraction: To do this, multiply the whole number (3) by the denominator (2), add the numerator (1), and keep the same denominator. This gives us (3 * 2) + 1 = 7/2.
-
Step 2: Multiply the fractions: Now we have the problem: 1/2 * 7/2. To multiply fractions, simply multiply the numerators together and the denominators together. This gives us (1 * 7) / (2 * 2) = 7/4.
-
Step 3: Simplify or Convert to a Mixed Number: The improper fraction 7/4 can be simplified into a mixed number by dividing the numerator by the denominator. 7 divided by 4 is 1 with a remainder of 3. Therefore, 7/4 is equivalent to 1 3/4.
Therefore, 1/2 of 3 1/2 is 1 3/4.
Method 2: Distributive Property
Another approach involves using the distributive property of multiplication. This method is particularly helpful when dealing with more complex mixed numbers.
-
Step 1: Separate the whole number and fraction: We can rewrite 3 1/2 as 3 + 1/2.
-
Step 2: Distribute 1/2: Now, we multiply 1/2 by both parts of the expression: (1/2 * 3) + (1/2 * 1/2).
-
Step 3: Calculate each multiplication: (1/2 * 3) = 3/2 and (1/2 * 1/2) = 1/4.
-
Step 4: Add the results: Now, add the two resulting fractions: 3/2 + 1/4. To add these, we need a common denominator, which is 4. So we convert 3/2 to 6/4. Then, 6/4 + 1/4 = 7/4.
-
Step 5: Simplify or Convert to a Mixed Number: Again, 7/4 simplifies to 1 3/4.
Method 3: Visual Representation
A visual approach can be helpful for a deeper understanding, especially for those who are visually-oriented learners. Imagine a rectangle representing 3 1/2 units. To find half of this, divide the rectangle into two equal parts. Each half will represent 1 3/4 units. This visual representation confirms our previous calculations.
Method 4: Decimal Conversion
We can also solve this problem by converting the mixed numbers into decimals.
-
Step 1: Convert to decimals: 3 1/2 is equivalent to 3.5.
-
Step 2: Multiply by 0.5: Multiply 3.5 by 0.5 (which is the decimal equivalent of 1/2): 3.5 * 0.5 = 1.75
-
Step 3: Convert back to a fraction (optional): 1.75 can be written as 1 and 75/100, which simplifies to 1 and 3/4.
Explanation: Why These Methods Work
All four methods presented above are mathematically sound and arrive at the same correct answer. They demonstrate different approaches to working with fractions and mixed numbers, highlighting the flexibility and interconnectedness of mathematical concepts. The core principle lies in the understanding of fractions as parts of a whole and the application of fundamental arithmetic operations – multiplication and addition. The conversion to improper fractions ensures consistent application of the multiplication rule for fractions, while the distributive property allows for a more strategic approach by breaking down the problem into simpler steps. The visual representation aids in understanding the concept intuitively, while the decimal conversion offers an alternative approach particularly useful when using calculators.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to solve this? A: Yes, you can input the calculation as (1/2) * (3 + 1/2) or 0.5 * 3.5 into a calculator to get the answer directly as 1.75. Remember to convert this back to a fraction if needed.
-
Q: Why is it important to learn different methods for solving this problem? A: Understanding multiple approaches enhances your mathematical fluency and problem-solving skills. Different methods might be more efficient or intuitive depending on the complexity of the problem and your personal strengths.
-
Q: What if the problem was 1/3 of 3 1/2? A: You'd follow the same principles, converting to improper fractions (1/3 * 7/2 = 7/6 or 1 1/6), using the distributive property, or converting to decimals (0.333... * 3.5 ≈ 1.166...). The core principles remain the same.
-
Q: Are there any real-world applications of this type of calculation? A: Absolutely! This type of calculation is fundamental in various applications, including cooking (halving a recipe), budgeting (splitting costs), construction (measuring materials), and numerous other scenarios involving fractions and proportions.
Conclusion: Mastering Fractions – A Building Block for Success
Calculating 1/2 of 3 1/2, while seemingly simple, offers a valuable opportunity to reinforce foundational mathematical skills. Understanding the different methods, from converting to improper fractions to using the distributive property, not only helps in solving this specific problem but builds a strong foundation for tackling more complex mathematical challenges. Mastering fractions is crucial for success in higher-level mathematics and its numerous real-world applications. Through consistent practice and a grasp of these fundamental principles, you can confidently navigate the world of fractions and proportions. Remember, the key to mathematical proficiency lies in understanding the why behind the how.
Latest Posts
Latest Posts
-
500 G To Oz
Sep 14, 2025
-
Sedaris Me Talk Pretty
Sep 14, 2025
-
178 Pounds In Kilos
Sep 14, 2025
-
5 Divided By 95
Sep 14, 2025
-
28 35 As A Percent
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Of 3 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.