28/35 As A Percent
renascent
Sep 14, 2025 · 5 min read
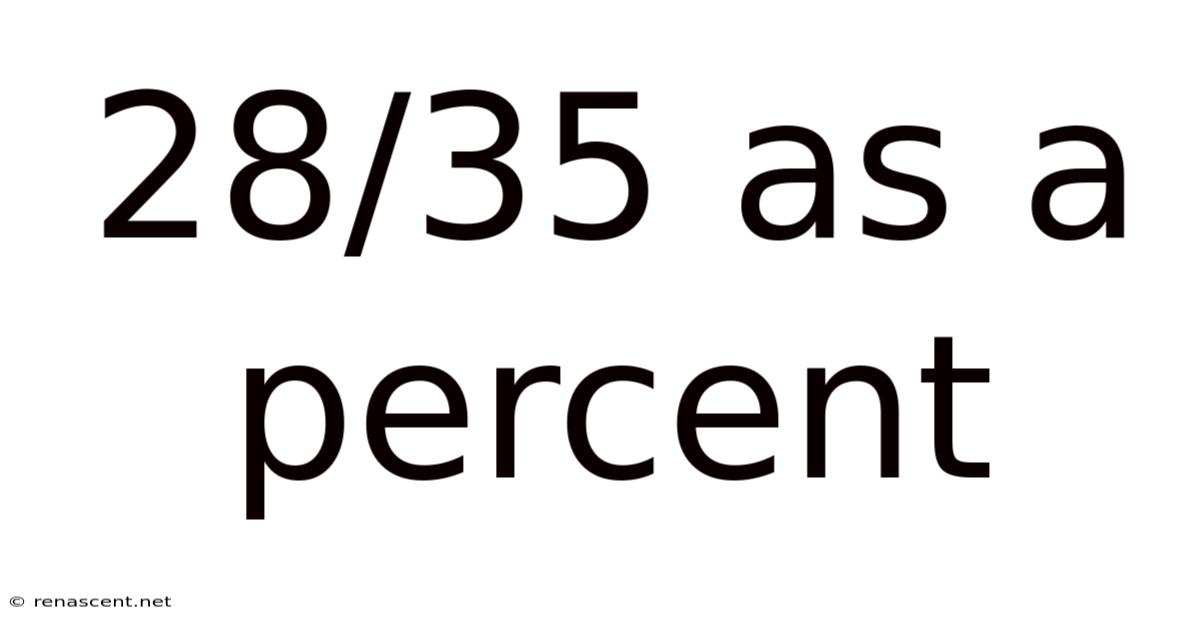
Table of Contents
Understanding 28/35 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from calculating grades and discounts to understanding financial reports and statistical data. This comprehensive guide will delve into the process of converting the fraction 28/35 into a percentage, explaining the underlying principles and providing practical examples. We'll also explore related concepts and answer frequently asked questions to ensure a complete understanding of this essential mathematical operation.
Introduction: Fractions, Decimals, and Percentages
Before we tackle the specific conversion of 28/35, let's briefly review the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator/denominator). For example, 28/35 represents 28 parts out of a total of 35 parts.
-
Decimal: A decimal is a way of expressing a fraction using a base-10 system. The decimal point separates the whole number from the fractional part.
-
Percentage: A percentage represents a fraction or decimal as parts per hundred. The symbol "%" signifies "per hundred." For instance, 50% means 50 parts out of 100.
The ability to convert between these three forms is crucial for solving many mathematical problems.
Converting 28/35 to a Percentage: Step-by-Step Guide
There are two primary methods for converting the fraction 28/35 to a percentage:
Method 1: Simplifying the Fraction and then Converting
This method involves simplifying the fraction to its lowest terms before converting it to a percentage. This often makes the calculation easier.
-
Simplify the Fraction: Find the greatest common divisor (GCD) of 28 and 35. The GCD of 28 and 35 is 7. Divide both the numerator and the denominator by 7:
28 ÷ 7 = 4 35 ÷ 7 = 5
This simplifies the fraction to 4/5.
-
Convert to a Decimal: Divide the numerator (4) by the denominator (5):
4 ÷ 5 = 0.8
-
Convert to a Percentage: Multiply the decimal by 100 and add the "%" symbol:
0.8 × 100 = 80%
Therefore, 28/35 simplifies to 4/5, which is equivalent to 0.8 or 80%.
Method 2: Direct Conversion to Percentage
This method involves directly converting the fraction to a percentage without simplifying first.
-
Convert to a Decimal: Divide the numerator (28) by the denominator (35):
28 ÷ 35 = 0.8
-
Convert to a Percentage: Multiply the decimal by 100 and add the "%" symbol:
0.8 × 100 = 80%
This method yields the same result: 80%. While this method might seem quicker, simplifying the fraction first can often simplify the division, particularly with larger numbers.
Understanding the Result: 80%
The result, 80%, signifies that 28 is 80% of 35. This means that if you divide 35 into 100 equal parts, 28 would represent 80 of those parts.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages has numerous practical applications:
-
Calculating Grades: If you answered 28 out of 35 questions correctly on a test, your grade would be 80%.
-
Determining Discounts: A store offering an 80% discount on an item means the price is reduced by 80% of its original value.
-
Analyzing Financial Data: Understanding percentages is crucial for interpreting financial statements, such as profit margins and interest rates.
-
Interpreting Statistical Data: Percentages are widely used to represent data in surveys, polls, and scientific studies.
Further Exploration: Related Concepts
Understanding percentage conversions is interconnected with other mathematical concepts:
-
Ratios and Proportions: Fractions represent ratios, and converting them to percentages involves understanding proportions.
-
Decimals and Scientific Notation: The conversion process often involves working with decimals and understanding how to express numbers in different forms.
-
Percentage Increase and Decrease: Understanding percentages is fundamental to calculating percentage changes (increases or decreases) in values over time.
Frequently Asked Questions (FAQ)
-
Q: What if the fraction is an improper fraction (numerator larger than denominator)?
A: Convert the improper fraction into a mixed number (whole number and fraction), then convert the fractional part to a decimal and then a percentage. Add the whole number to the resulting percentage.
-
Q: Can I use a calculator for this conversion?
A: Yes, most calculators can perform division and multiplication, allowing for a direct conversion.
-
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare and interpret fractions and decimals, making them easier to understand and apply in various real-world situations.
-
Q: Are there other methods to convert fractions to percentages?
A: While the methods described are the most common, you can also use proportions to solve this type of problem. For example, you could set up the proportion: 28/35 = x/100 and solve for x.
Conclusion: Mastering Percentage Conversions
Converting fractions like 28/35 to percentages is a valuable skill with widespread applications. By understanding the underlying principles and employing the step-by-step methods outlined above, you can confidently perform these conversions and apply this knowledge to solve problems in various contexts. Remember to practice regularly to reinforce your understanding and improve your speed and accuracy. With consistent practice, you'll become proficient in converting fractions to percentages and confidently navigate mathematical problems involving percentages. The key is to understand the underlying concept of representing parts of a whole and to apply the appropriate mathematical operations – division and multiplication – to achieve the desired result.
Latest Posts
Latest Posts
-
Reflector Vs Refractor Telescope
Sep 14, 2025
-
7 5 In Fraction Form
Sep 14, 2025
-
1300 Divided By 3
Sep 14, 2025
-
Mg To Ml Syringe
Sep 14, 2025
-
36 1 C In F
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 28/35 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.