1/4 As A Percentage
renascent
Sep 22, 2025 · 5 min read
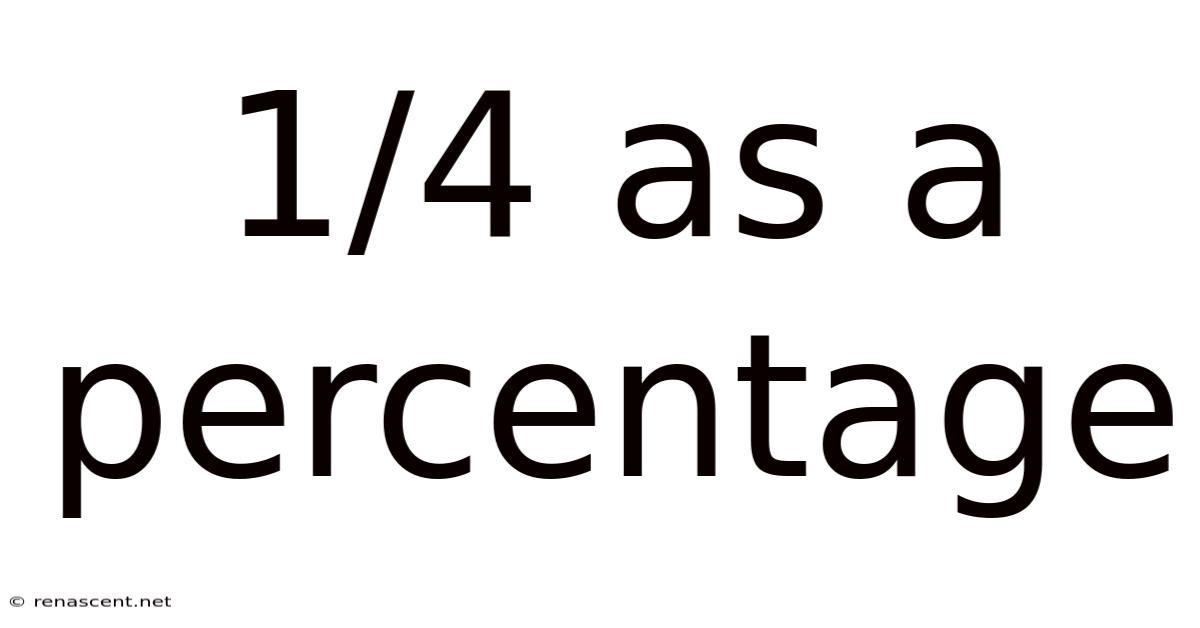
Table of Contents
Understanding 1/4 as a Percentage: A Comprehensive Guide
Knowing how to convert fractions to percentages is a fundamental skill in mathematics with applications across various fields, from everyday budgeting to advanced statistical analysis. This comprehensive guide will delve into the conversion of the fraction 1/4 to a percentage, explaining the process in detail and exploring its practical implications. We'll move beyond the simple conversion and explore the underlying mathematical principles, providing you with a robust understanding of this concept.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before we dive into the specifics of 1/4, let's establish the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole. A fraction shows a part of a whole as a ratio (e.g., 1/4 means one part out of four equal parts). A decimal expresses a part of a whole as a number based on powers of ten (e.g., 0.25). A percentage represents a part of a whole as a number out of 100 (e.g., 25%). They are all interchangeable, allowing us to express the same value in different formats depending on the context.
Converting 1/4 to a Percentage: Step-by-Step Guide
The conversion of 1/4 to a percentage involves two straightforward steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, you divide the numerator (the top number) by the denominator (the bottom number). In this case:
1 ÷ 4 = 0.25
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%).
0.25 x 100 = 25%
Therefore, 1/4 is equal to 25%.
Visualizing 1/4 as a Percentage
Imagine a pie cut into four equal slices. One slice represents 1/4 of the pie. If you were to divide the pie into 100 equal pieces instead, 25 of those pieces would be equivalent to the size of one of the original four slices. This visually demonstrates that 1/4 and 25% represent the same proportion of the whole.
The Mathematical Rationale Behind the Conversion
The process of converting fractions to percentages is based on the fundamental principle that a percentage is always a fraction with a denominator of 100. When we multiply a decimal by 100, we are essentially scaling it up to express it as a fraction with a denominator of 100. For example:
0.25 can be written as 25/100, which is equivalent to 25%.
This mathematical relationship allows for seamless conversion between fractions, decimals, and percentages.
Practical Applications of Understanding 1/4 as a Percentage
Understanding the equivalence of 1/4 and 25% has numerous practical applications in various aspects of life:
-
Everyday Calculations: Calculating discounts, tips, or sales tax often involves working with percentages. Knowing that 1/4 is equivalent to 25% allows for quick mental estimations. For instance, a 25% discount on a $100 item is easily calculated as $100 x 0.25 = $25.
-
Financial Literacy: Understanding percentages is crucial for managing personal finances. Analyzing interest rates, loan repayments, and investment returns often involves working with fractions and percentages. Converting between the two makes these calculations more manageable.
-
Data Analysis and Statistics: In statistics and data analysis, percentages are frequently used to represent proportions and probabilities. Converting fractions to percentages makes it easier to interpret and visualize data.
-
Cooking and Baking: Recipes often use fractions to indicate ingredient quantities. Understanding the percentage equivalent can aid in adjusting recipes or scaling them up or down. For example, if a recipe calls for 1/4 cup of sugar, you know that this is equivalent to 25% of a cup.
Beyond 1/4: Extending the Concept to Other Fractions
The method of converting fractions to percentages isn't limited to 1/4. The same principles can be applied to any fraction. For example:
- 1/2: 1 ÷ 2 = 0.5; 0.5 x 100 = 50%
- 3/4: 3 ÷ 4 = 0.75; 0.75 x 100 = 75%
- 1/5: 1 ÷ 5 = 0.2; 0.2 x 100 = 20%
- 2/3: 2 ÷ 3 ≈ 0.6667; 0.6667 x 100 ≈ 66.67% (Note: This results in a recurring decimal, highlighting that not all fractions convert to neat percentages.)
Frequently Asked Questions (FAQ)
-
Q: Why is it important to understand the relationship between fractions and percentages?
-
A: Understanding this relationship is crucial for performing various calculations and interpreting data accurately in diverse fields, from finance to cooking. It enhances numerical literacy and allows for flexible problem-solving.
-
Q: Can all fractions be easily converted to percentages?
-
A: No. While many fractions convert to neat percentages, some result in recurring or non-terminating decimals, making the percentage representation an approximation.
-
Q: Are there any shortcuts for converting fractions to percentages?
-
A: For simple fractions like 1/4, 1/2, 3/4, memorizing the percentage equivalents is helpful. However, the general method of dividing the numerator by the denominator and multiplying by 100 remains the most reliable approach for all fractions.
-
Q: How can I improve my skills in converting fractions and percentages?
-
A: Practice is key! Try converting various fractions to percentages and vice versa. Use online calculators or worksheets for practice and to check your answers.
Conclusion: Mastering the Conversion of 1/4 and Beyond
Understanding the conversion of 1/4 to 25% is a fundamental step in developing a strong grasp of mathematical concepts related to fractions and percentages. This skill transcends simple calculations, enhancing your ability to interpret data, analyze situations, and solve problems in various contexts. By grasping the underlying mathematical principles and applying the step-by-step process outlined in this guide, you can confidently navigate these concepts and apply them to various real-world situations. Remember, the ability to convert between fractions and percentages is a valuable skill that will benefit you throughout your life. Consistent practice and a clear understanding of the underlying principles will solidify your comprehension and make this skill second nature.
Latest Posts
Latest Posts
-
8000 Hours To Days
Sep 22, 2025
-
24 Divided By 3
Sep 22, 2025
-
Latitude Of Darwin Australia
Sep 22, 2025
-
Example Of A Wedge
Sep 22, 2025
-
50 G Peanuts Protein
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1/4 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.