1/4 Divided By 2
renascent
Sep 17, 2025 · 5 min read
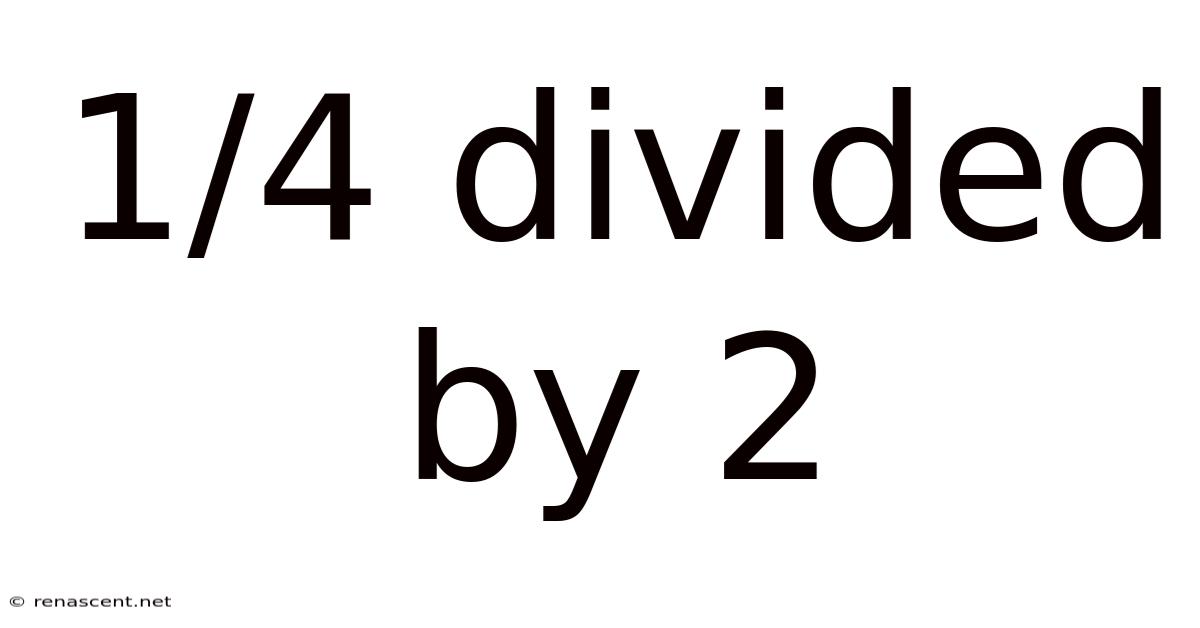
Table of Contents
Understanding 1/4 Divided by 2: A Deep Dive into Fraction Division
This article explores the seemingly simple problem of 1/4 divided by 2, delving far beyond the basic answer to unpack the underlying principles of fraction division. We’ll cover various methods for solving this problem, explain the underlying mathematical reasoning, and address common misconceptions. This will provide a comprehensive understanding, beneficial for students learning fractions, teachers needing supplementary teaching materials, and anyone curious about the intricacies of mathematics.
Introduction: Deconstructing the Problem
The question, "What is 1/4 divided by 2?", might seem trivial at first glance. However, mastering fraction division is crucial for a solid foundation in mathematics. This problem allows us to explore fundamental concepts that extend to more complex calculations involving fractions, decimals, and even algebra. Understanding this simple division problem unlocks a deeper appreciation for how fractions interact within mathematical operations. We will cover different approaches to solving this, solidifying your understanding of the process and its implications.
Method 1: The "Keep, Change, Flip" Method
This is perhaps the most popular method for dividing fractions, and it works wonders for this problem. The method is commonly remembered by the mnemonic "Keep, Change, Flip," or KCF.
- Keep: Keep the first fraction (the dividend) exactly as it is: 1/4.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) – this means finding its reciprocal. The reciprocal of 2 (which can be written as 2/1) is 1/2.
So, our problem transforms from:
1/4 ÷ 2 becomes 1/4 × 1/2
- Multiply: Now, simply multiply the numerators together and the denominators together:
(1 × 1) / (4 × 2) = 1/8
Therefore, 1/4 divided by 2 equals 1/8.
Method 2: Visual Representation Using Fraction Bars
A visual approach can help solidify understanding, especially for those who benefit from concrete examples. Imagine a fraction bar representing 1/4. Now, we need to divide this 1/4 into two equal parts. This visually demonstrates that each resulting part represents 1/8 of the whole.
[Imagine a visual here: A bar divided into four equal sections, with one section shaded. Then, the shaded section is further divided in half, showcasing the resulting 1/8.]
Method 3: Understanding Division as Repeated Subtraction
Division can be viewed as repeated subtraction. How many times can we subtract 2 from 1/4? This approach is less intuitive with fractions, but it helps illustrate the concept of division. We can't directly subtract 2 from 1/4 because 2 is larger. Instead, let's consider dividing 1/4 into smaller portions. Dividing by 2 is equivalent to finding half of 1/4. Half of 1/4 is indeed 1/8.
Method 4: Converting to Decimals (An Alternative Approach)
While not strictly necessary for this problem, converting the fraction to a decimal can provide an alternative perspective.
- Convert the fraction: 1/4 is equal to 0.25.
- Perform decimal division: 0.25 ÷ 2 = 0.125
- Convert back to a fraction (if needed): 0.125 is equivalent to 1/8.
This method demonstrates the equivalence between fractions and decimals in performing division.
The Mathematical Rationale: Exploring the Concept of Reciprocals
The "Keep, Change, Flip" method isn't just a trick; it's based on the properties of reciprocals and multiplication. Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by switching the numerator and the denominator. This is why we "flip" the second fraction. This underlying principle is crucial for understanding division of fractions more generally. It highlights the interconnectedness of mathematical operations, demonstrating how division and multiplication are fundamentally related.
Extending the Concept: More Complex Fraction Division Problems
Understanding 1/4 ÷ 2 forms a solid foundation for tackling more complex fraction division problems. The same principles apply, whether you are dividing two fractions, a fraction by a whole number, or a whole number by a fraction. The "Keep, Change, Flip" method consistently offers a reliable and efficient way to solve these problems. The ability to confidently handle fraction division enhances mathematical proficiency across various contexts, from simple arithmetic to complex algebraic equations.
Addressing Common Misconceptions
A common mistake is to simply divide the numerator by the whole number, leaving the denominator unchanged. This leads to an incorrect answer. It is crucial to understand that dividing a fraction by a whole number requires considering the whole fraction, not just the numerator. Remember that the "Keep, Change, Flip" method correctly accounts for the whole fractional value.
Frequently Asked Questions (FAQ)
-
Q: Why does the "Keep, Change, Flip" method work? A: It's based on the mathematical property that dividing by a number is the same as multiplying by its reciprocal.
-
Q: Can I use this method for dividing any two fractions? A: Yes, the "Keep, Change, Flip" method works for dividing any two fractions.
-
Q: What if I'm dividing a whole number by a fraction? A: Consider the whole number as a fraction (e.g., 5 becomes 5/1) and then apply the "Keep, Change, Flip" method.
-
Q: Is there another way to solve 1/4 divided by 2 besides KCF? A: Yes, as explained above, you can use visual representation, repeated subtraction (though less practical with fractions), or conversion to decimals.
-
Q: What are some real-world applications of fraction division? A: Fraction division is used in various areas like baking (dividing ingredients), construction (measuring materials), and sewing (cutting fabric).
Conclusion: Mastering Fraction Division
Solving 1/4 divided by 2 is more than just finding the answer; it's about understanding the fundamental principles of fraction division. By exploring various methods, understanding the concept of reciprocals, and recognizing potential pitfalls, you gain a more profound appreciation of how fractions work. This foundational knowledge paves the way for tackling more advanced mathematical concepts with confidence and accuracy. Remember the "Keep, Change, Flip" method, visualize when possible, and always strive for a deeper understanding of the underlying mathematical rationale. This will not only help you solve fraction division problems but also significantly enhance your mathematical skills overall. Mastering this seemingly simple concept opens doors to more complex mathematical challenges, ensuring a strong foundation for future learning.
Latest Posts
Latest Posts
-
30 Mins From Now
Sep 17, 2025
-
Average Temperature Japan 1945
Sep 17, 2025
-
4 8 K In Numbers
Sep 17, 2025
-
1 3 Of 120
Sep 17, 2025
-
115 Lbs In Kg
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.