1/5 In A Percent
renascent
Sep 17, 2025 · 6 min read
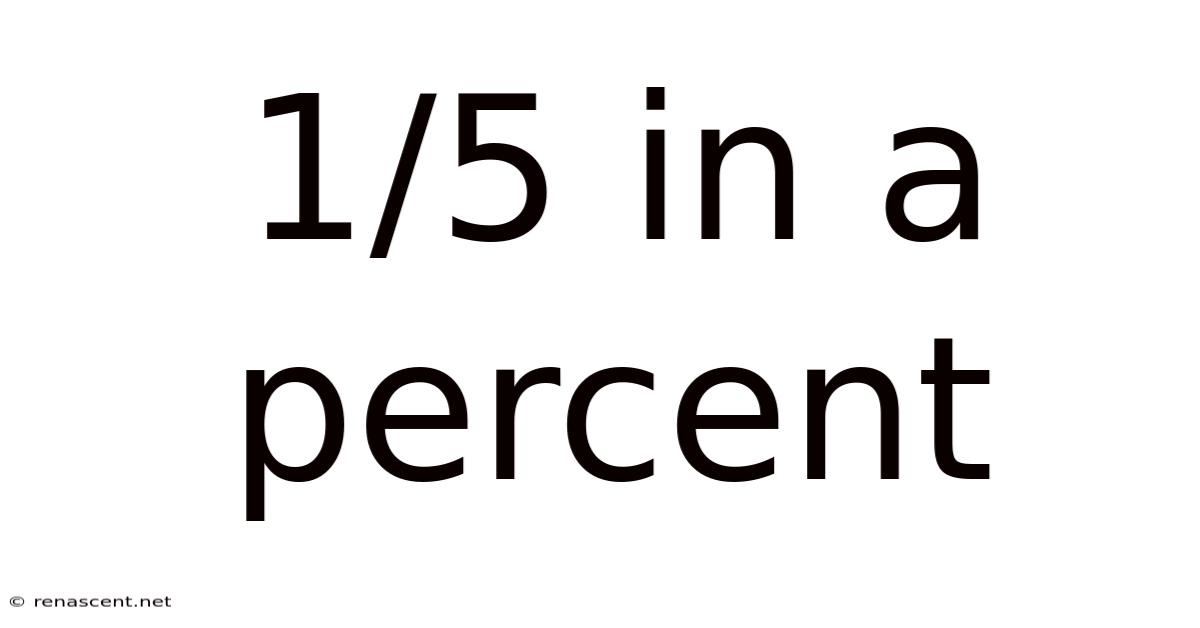
Table of Contents
Understanding 1/5 as a Percent: A Comprehensive Guide
Fractions and percentages are fundamental concepts in mathematics with widespread applications in everyday life. Converting fractions to percentages is a crucial skill, and understanding how to do so accurately is essential for various tasks, from calculating discounts to understanding financial reports. This article will comprehensively explore how to convert the fraction 1/5 into a percentage, delving into the underlying principles and providing practical examples. We'll cover various methods, explain the underlying mathematical reasoning, and address frequently asked questions. By the end, you'll not only know that 1/5 is 20%, but you'll also understand why and be able to apply this knowledge to other fractional conversions.
Understanding Fractions and Percentages
Before we dive into the conversion of 1/5, let's establish a clear understanding of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 1/5, the numerator is 1, and the denominator is 5, meaning we have 1 part out of a total of 5 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 make up the whole. For instance, 20% means 20 parts out of 100. Percentages are a convenient way to express proportions and comparisons, especially in contexts involving rates, discounts, and statistics.
Method 1: Converting 1/5 to a Decimal, then to a Percentage
This is a common and straightforward approach. We first convert the fraction 1/5 into a decimal by dividing the numerator by the denominator:
1 ÷ 5 = 0.2
Now that we have the decimal equivalent (0.2), converting it to a percentage is simple. We multiply the decimal by 100 and add the percentage symbol:
0.2 x 100 = 20%
Therefore, 1/5 is equal to 20%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method relies on the fundamental principle of equivalent fractions. We aim to find a fraction equivalent to 1/5 but with a denominator of 100. To do this, we need to determine what number we multiply the denominator (5) by to get 100:
100 ÷ 5 = 20
Since we multiply the denominator by 20, we must also multiply the numerator by the same number to maintain the equivalence:
1 x 20 = 20
So, our equivalent fraction is 20/100. Since a percentage is a fraction out of 100, 20/100 directly translates to 20%.
Method 3: Using Proportions
Proportions offer another way to solve this problem. We can set up a proportion to find the percentage equivalent of 1/5:
1/5 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
1 * 100 = 5 * x
100 = 5x
Now, divide both sides by 5:
x = 100 ÷ 5 = 20
Therefore, x = 20, meaning 1/5 is equal to 20%.
The Mathematical Reasoning Behind the Conversion
The core concept behind converting fractions to percentages is the idea of expressing a part of a whole as a fraction of 100. We utilize the principles of equivalent fractions and proportions to achieve this. Multiplying a fraction by 100/1 (which is equal to 1 and therefore doesn't change the value) essentially scales the fraction to express it as a number out of 100, directly representing the percentage.
Practical Applications of Converting 1/5 to a Percentage
Understanding that 1/5 equals 20% has numerous practical applications:
- Discounts: A 1/5 discount on an item means a 20% discount.
- Surveys and Statistics: If 1/5 of respondents chose a particular option, it signifies a 20% response rate.
- Financial Calculations: Understanding proportions in finance, such as profit margins or interest rates, often involves converting fractions to percentages.
- Recipe Scaling: If a recipe calls for 1/5 of a cup of an ingredient, understanding that's equivalent to 20% can make scaling the recipe easier.
Extending the Concept: Converting Other Fractions to Percentages
The methods described above are applicable to converting any fraction into a percentage. For example:
- 1/2: 1 ÷ 2 = 0.5; 0.5 x 100 = 50%
- 1/4: 1 ÷ 4 = 0.25; 0.25 x 100 = 25%
- 3/4: 3 ÷ 4 = 0.75; 0.75 x 100 = 75%
- 2/5: 2 ÷ 5 = 0.4; 0.4 x 100 = 40%
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn how to convert fractions to percentages?
A1: Converting fractions to percentages is crucial for understanding proportions, comparing different quantities, and solving real-world problems in various fields, including finance, statistics, and everyday life situations like calculating discounts and understanding survey results.
Q2: Can I convert any fraction to a percentage?
A2: Yes, you can convert any fraction to a percentage using the methods described above. However, some fractions may result in repeating decimals when converted to decimals, leading to slightly less precise percentage representations.
Q3: What if the fraction is an improper fraction (numerator > denominator)?
A3: The process remains the same. You divide the numerator by the denominator to get the decimal equivalent, then multiply by 100 to obtain the percentage. The resulting percentage will be greater than 100%. For example, 5/2 = 2.5; 2.5 x 100 = 250%.
Q4: Are there any online tools to help with fraction to percentage conversion?
A4: Yes, many online calculators and converters are readily available to assist with converting fractions to percentages. These tools can be particularly helpful for more complex fractions. However, understanding the underlying mathematical principles is still crucial for developing strong mathematical skills.
Q5: What if I have a mixed number (a whole number and a fraction)?
A5: First, convert the mixed number to an improper fraction. Then, follow the same steps as described above to convert the improper fraction to a percentage. For example, 1 1/4 becomes 5/4; 5 ÷ 4 = 1.25; 1.25 x 100 = 125%.
Conclusion
Converting 1/5 to a percentage, yielding 20%, is a fundamental skill in mathematics. Understanding the different methods—conversion to decimals, finding equivalent fractions, and using proportions—provides a solid foundation for tackling similar conversions. This knowledge has widespread applications in numerous aspects of life, from calculating discounts to interpreting data and making informed decisions. Mastering this skill enhances your numeracy and problem-solving abilities, making you better equipped to handle quantitative information effectively. Remember to practice regularly to reinforce your understanding and build confidence in your mathematical skills.
Latest Posts
Latest Posts
-
9 X 3 2
Sep 17, 2025
-
6 Groups Of 5
Sep 17, 2025
-
Adr Approved Steering Wheels
Sep 17, 2025
-
What Does Ogn Mean
Sep 17, 2025
-
7 5 To A Fraction
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1/5 In A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.