9 X 3 2
renascent
Sep 17, 2025 · 6 min read
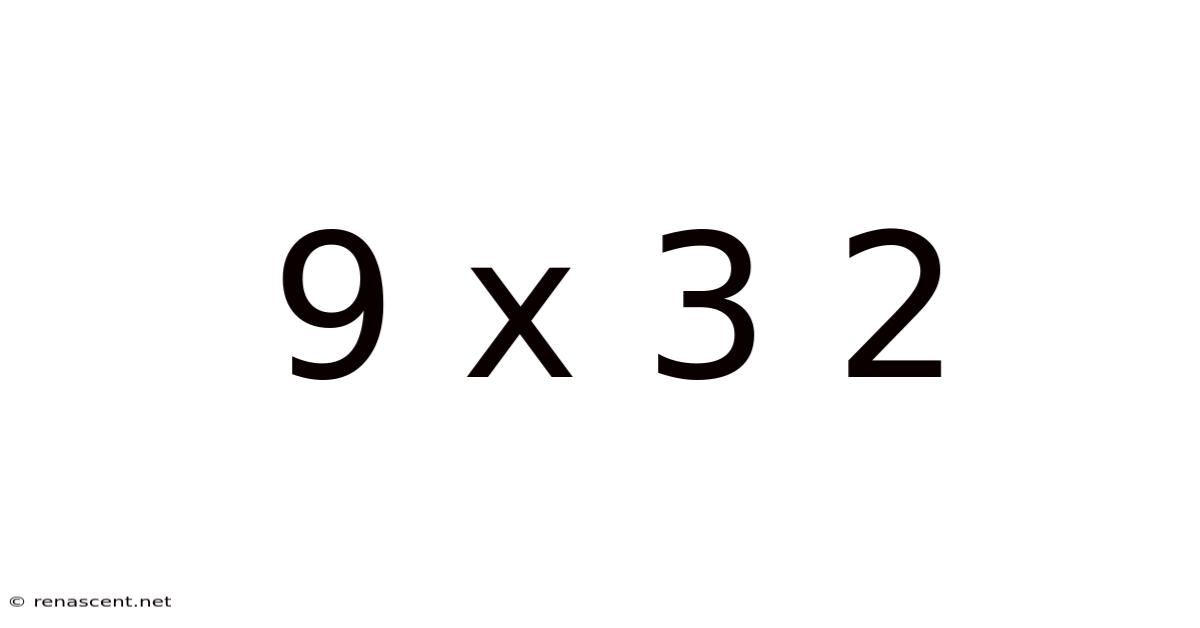
Table of Contents
Decoding 9 x 3 x 2: Exploring Multiplication, Factorization, and Beyond
This seemingly simple arithmetic expression, 9 x 3 x 2, opens doors to a surprisingly rich exploration of mathematical concepts. It's more than just a straightforward multiplication problem; it's a gateway to understanding fundamental principles of arithmetic, factorization, and even the beginnings of abstract algebra. This article will delve into the various facets of 9 x 3 x 2, providing a comprehensive understanding suitable for learners of all levels.
Introduction: A Basic Calculation and its Implications
At its core, 9 x 3 x 2 represents a series of multiplications. The answer, 54, is easily obtained through sequential calculations: 9 multiplied by 3 equals 27, and 27 multiplied by 2 equals 54. However, the simplicity of this calculation belies the deeper mathematical concepts that can be explored. We will examine this seemingly simple equation through the lenses of order of operations, factorization, prime numbers, and the commutative and associative properties of multiplication. Understanding these principles is crucial for developing a strong foundation in mathematics.
Understanding the Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which calculations should be performed. In our example, 9 x 3 x 2, there are no parentheses or exponents, so we simply proceed from left to right, performing the multiplications sequentially. This highlights the importance of understanding the order in which calculations are carried out to arrive at the correct answer, especially in more complex mathematical expressions.
Factorization: Breaking Down the Numbers
Factorization involves expressing a number as a product of its factors. The number 54 can be factored in several ways:
- 2 x 27: This reflects the last step in our sequential calculation.
- 3 x 18: This shows a different factorization, highlighting the factors 3 and 18.
- 6 x 9: This factorization highlights the factors 6 and 9.
- 2 x 3 x 3 x 3: This is the prime factorization of 54.
Prime factorization is particularly important because it represents a unique decomposition of a number into its prime factors (numbers divisible only by 1 and themselves). In this case, 2 and 3 are the prime factors of 54. The prime factorization of a number is fundamental in various areas of mathematics, including simplifying fractions, finding greatest common divisors (GCD), and least common multiples (LCM).
The Commutative and Associative Properties of Multiplication
Multiplication possesses two important properties:
-
Commutative Property: This states that the order of the numbers being multiplied does not affect the result. Therefore, 9 x 3 x 2 is the same as 3 x 9 x 2, 2 x 9 x 3, and so on. The order can be rearranged without altering the final answer (54).
-
Associative Property: This states that the grouping of numbers being multiplied does not affect the result. For example, (9 x 3) x 2 is equal to 9 x (3 x 2). Both yield 54. This property allows for flexibility in how we approach the calculation.
Exploring the Individual Factors: 9, 3, and 2
Let's examine the individual factors:
-
9: A composite number (not prime), it is a perfect square (3 x 3) and is divisible by 1, 3, and 9. It is also a multiple of 3.
-
3: A prime number, meaning it's only divisible by 1 and itself. It’s a fundamental building block in number theory.
-
2: Another prime number. The only even prime number. It plays a crucial role in many mathematical concepts, including even and odd numbers and divisibility rules.
Understanding the properties of these individual factors enhances our understanding of the overall calculation.
Geometric Representation
The equation 9 x 3 x 2 can also be visualized geometrically. Imagine a rectangular prism with dimensions 9 units long, 3 units wide, and 2 units high. The volume of this prism would be 54 cubic units, representing the result of the multiplication. This illustrates how multiplication can be applied to real-world scenarios involving area and volume calculations.
Applications in Real-World Scenarios
The seemingly simple calculation 9 x 3 x 2 has practical applications in various fields:
- Everyday Calculations: Calculating the total cost of 9 items costing $3 each, purchased in 2 sets.
- Measurement and Geometry: Determining the volume of a container or the area of a surface.
- Computer Programming: Used in loops and array manipulations.
- Engineering and Physics: Calculating forces, distances, or volumes in various engineering and physics problems.
These examples demonstrate how even simple arithmetic operations have a broad range of applications.
Extending the Concept: Exploring Larger Multiplications
We can expand on this concept by considering larger multiplications. Imagine if the expression was 9 x 3 x 2 x 5. The process remains the same; we simply multiply sequentially or use the commutative and associative properties to rearrange and group the factors for easier calculation. This demonstrates how the fundamental principles explored here can be applied to more complex calculations. This introduces the concept of scaling the problem, a key aspect in many mathematical and scientific fields.
Advanced Applications: Number Theory and Abstract Algebra
At a more advanced level, the prime factorization of 54 (2 x 3 x 3 x 3) has significance in number theory. It helps in determining the number of divisors of 54, finding the greatest common divisor (GCD) and least common multiple (LCM) with other numbers, and exploring various number theoretic functions. In abstract algebra, the concept of factorization and prime numbers extends to more abstract algebraic structures and has far-reaching implications in advanced mathematics.
Frequently Asked Questions (FAQ)
-
Q: Can I change the order of the numbers in 9 x 3 x 2? A: Yes, due to the commutative property of multiplication, changing the order does not change the final result. You will still get 54.
-
Q: What is the prime factorization of 54? A: The prime factorization of 54 is 2 x 3 x 3 x 3 (or 2 x 3³).
-
Q: What if there were parentheses in the expression? A: Parentheses would dictate the order of operations. For example, (9 x 3) x 2 would be calculated as 27 x 2 = 54, which is the same result. However, 9 x (3 x 2) would also be calculated as 9 x 6 = 54.
-
Q: How can I use this in real life? A: The concepts explained can be applied in countless real-life situations, from simple calculations like determining total cost to more complex scenarios in engineering, physics, and computer science.
Conclusion: More Than Just a Simple Equation
The seemingly simple equation 9 x 3 x 2 provides a rich learning opportunity. It's not just about obtaining the answer (54); it's about understanding the fundamental principles of arithmetic, including the order of operations, factorization, prime numbers, and the commutative and associative properties of multiplication. By exploring these concepts, we develop a stronger foundation in mathematics and learn to appreciate the interconnectedness of seemingly simple mathematical expressions with more complex mathematical ideas. The seemingly simple act of multiplying 9, 3, and 2 opens doors to a broader appreciation of the elegance and power of mathematics. From everyday calculations to advanced concepts in number theory and abstract algebra, this basic equation serves as a solid stepping stone to more intricate mathematical explorations.
Latest Posts
Latest Posts
-
500 Min To Hours
Sep 17, 2025
-
Jvc Ir Profile Number
Sep 17, 2025
-
24 Divided By 5
Sep 17, 2025
-
42 Divide By 6
Sep 17, 2025
-
Chuck Close Self Portrait
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 9 X 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.