1 9 X 180
renascent
Sep 18, 2025 · 5 min read
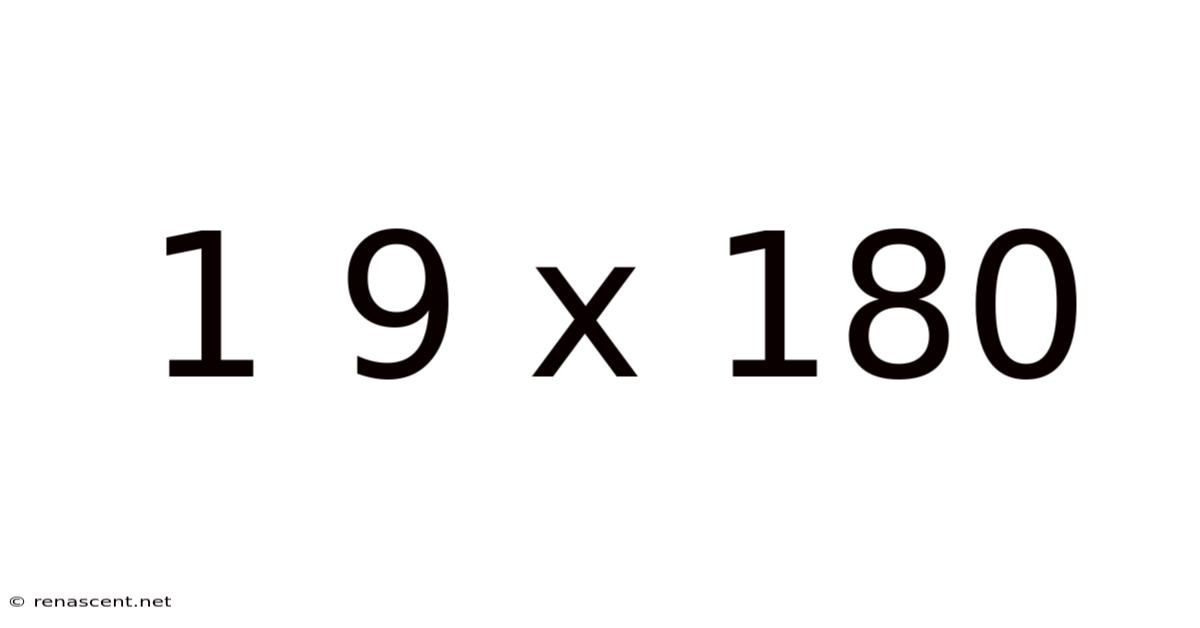
Table of Contents
Decoding 19 x 180: A Deep Dive into Multiplication and its Applications
Understanding multiplication is fundamental to mathematics and its applications span across numerous fields. This article delves into the seemingly simple calculation of 19 x 180, exploring various methods of solving it, its underlying mathematical principles, and its relevance in real-world scenarios. We’ll move beyond the basic answer to explore the deeper concepts and practical applications that make multiplication such a vital skill.
Introduction: More Than Just a Calculation
The multiplication problem 19 x 180 might seem straightforward, easily solvable with a calculator. However, understanding the process behind arriving at the solution is crucial. This goes beyond simple arithmetic; it’s about grasping the concept of repeated addition, distributive properties, and the underlying structure of our number system. This understanding forms the bedrock for more complex mathematical operations and problem-solving in various disciplines.
Methods for Solving 19 x 180
Several methods can be used to solve 19 x 180, each offering unique insights into the nature of multiplication:
1. Standard Multiplication Algorithm:
This is the most commonly taught method in schools. It involves multiplying each digit of 19 (the ones and tens digits) by each digit of 180 (the ones, tens, and hundreds digits) and then adding the partial products:
- Step 1: Multiply 19 by 0 (the ones digit of 180): 19 x 0 = 0
- Step 2: Multiply 19 by 8 (the tens digit of 180): 19 x 8 = 152 (write this down shifted one place to the left)
- Step 3: Multiply 19 by 1 (the hundreds digit of 180): 19 x 1 = 19 (write this down shifted two places to the left)
- Step 4: Add the partial products: 0 + 1520 + 1900 = 3420
Therefore, 19 x 180 = 3420
2. Distributive Property:
This method utilizes the distributive property of multiplication over addition. We can break down 19 into 20 - 1, making the calculation simpler:
- 19 x 180 = (20 - 1) x 180
- = (20 x 180) - (1 x 180)
- = 3600 - 180
- = 3420
This method showcases the flexibility of mathematical operations and how manipulating numbers can simplify calculations.
3. Mental Math Techniques:
With practice, mental math techniques can be used to solve this quickly. One approach is to multiply 19 by 18 and then multiply the result by 10:
- 19 x 18 = 342 (this might require some mental calculation or breaking down 18 into 10 + 8)
- 342 x 10 = 3420
This method emphasizes the importance of number sense and the ability to manipulate numbers efficiently.
4. Using a Calculator:
While using a calculator provides a quick answer, it's crucial to remember the underlying principles and the steps involved in the calculation. Calculators provide a tool for verification and for handling larger, more complex multiplications but shouldn't replace understanding the fundamental methods.
The Mathematical Principles Behind Multiplication
The seemingly simple operation of 19 x 180 relies on several core mathematical principles:
-
Repeated Addition: Multiplication is essentially repeated addition. 19 x 180 means adding 19 to itself 180 times.
-
Commutative Property: The order of multiplication doesn't affect the result. 19 x 180 is the same as 180 x 19.
-
Associative Property: The grouping of numbers in multiplication doesn't change the outcome. This property is particularly useful when dealing with more complex multiplications involving several numbers.
-
Distributive Property: As demonstrated earlier, this property allows us to break down numbers and simplify calculations.
Real-World Applications of Multiplication
The application of multiplication extends far beyond the classroom. Understanding this fundamental operation is crucial in numerous fields:
-
Business and Finance: Calculating profits, losses, discounts, taxes, interest rates, and budgeting all rely heavily on multiplication.
-
Engineering and Physics: Calculating forces, velocities, areas, volumes, and various physical quantities often involves multiplication.
-
Computer Science: Many algorithms and calculations within computer programs utilize multiplication as a core function.
-
Everyday Life: From calculating the total cost of groceries to determining the amount of paint needed to cover a wall, multiplication is a crucial part of daily life.
Expanding the Concept: Beyond 19 x 180
While we’ve focused on 19 x 180, the principles discussed are applicable to all multiplication problems. Consider these extensions:
-
Larger Numbers: The same methods can be applied to multiplying larger numbers. The standard algorithm, distributive property, and mental math techniques remain relevant, albeit potentially requiring more steps.
-
Decimal Numbers: Multiplying decimal numbers involves similar principles, but requires careful attention to the placement of the decimal point.
-
Fractions: Multiplying fractions involves multiplying the numerators and denominators separately.
-
Algebra: Multiplication is a fundamental operation in algebra, used extensively in solving equations, simplifying expressions, and working with polynomials.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to multiply 19 x 180?
A1: The easiest method depends on individual preferences and skills. For some, the standard algorithm is straightforward. For others, the distributive property might be more intuitive. Mental math techniques are also effective with practice.
Q2: Why is it important to learn different methods of multiplication?
A2: Learning multiple methods provides flexibility and adaptability. Different methods are more efficient in different situations, and understanding the underlying principles behind each method strengthens mathematical understanding.
Q3: How can I improve my multiplication skills?
A3: Practice is key! Regularly solving multiplication problems, using different methods, and focusing on mental math techniques will significantly improve your skills.
Conclusion: Mastering Multiplication for a Brighter Future
The seemingly simple calculation of 19 x 180 unveils a deeper understanding of mathematical principles and their vast applications. Mastering multiplication is not just about finding the correct answer; it’s about developing a robust understanding of number sense, problem-solving skills, and the ability to apply mathematical concepts to various real-world scenarios. By exploring different methods and understanding the underlying principles, you’ll build a solid foundation for more advanced mathematical concepts and applications in your academic and professional pursuits. The journey of learning mathematics is a continuous process of discovery, and understanding fundamental operations like multiplication is the crucial first step towards a brighter future.
Latest Posts
Latest Posts
-
Parts Of Brake Drum
Sep 18, 2025
-
2 10 X 6
Sep 18, 2025
-
Animals That Are Monogastric
Sep 18, 2025
-
37 1 Celsius To Fahrenheit
Sep 18, 2025
-
3 62 Kg In Pounds
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 9 X 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.