2 10 X 6
renascent
Sep 18, 2025 · 6 min read
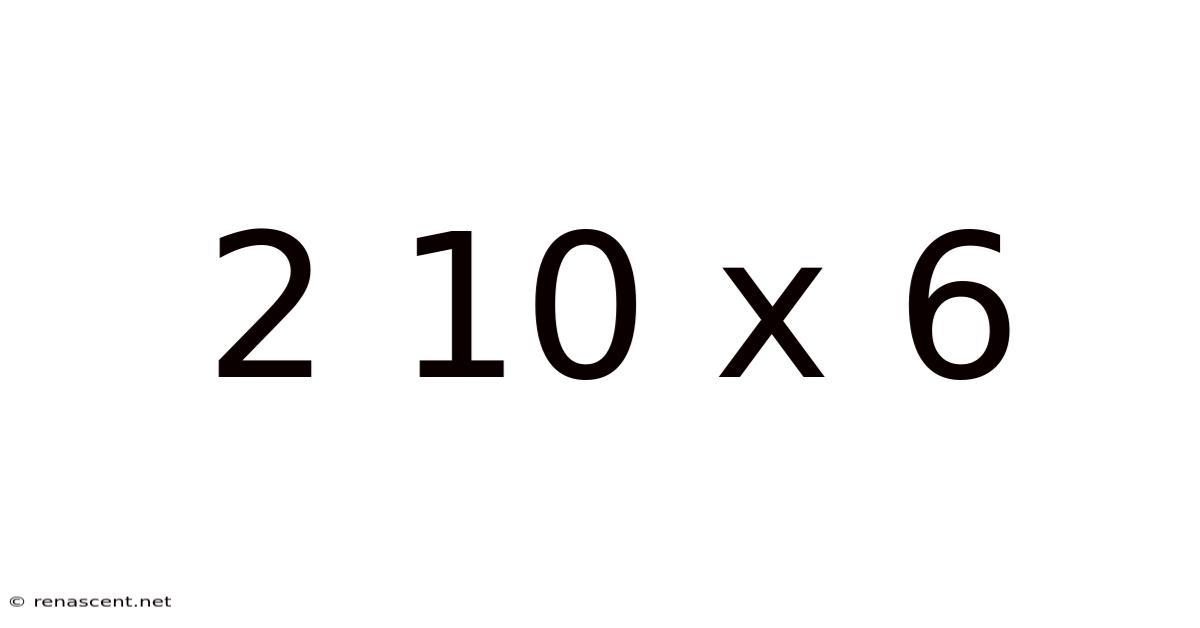
Table of Contents
Decoding 2 x 10 x 6: Exploring Dimensions, Volume, and Applications
The seemingly simple expression "2 x 10 x 6" represents much more than just a multiplication problem. It describes a three-dimensional space, defining dimensions that have numerous practical applications across various fields. Understanding this seemingly basic concept opens doors to comprehending volume calculations, spatial reasoning, and the practical implications of dimensions in real-world scenarios. This article will delve into the significance of 2 x 10 x 6, exploring its mathematical implications, real-world applications, and potential extensions to related concepts.
Understanding the Dimensions: Length, Width, and Height
The expression "2 x 10 x 6" typically represents the dimensions of a rectangular prism (or cuboid). In this case:
- 2 represents the length (or depth, depending on orientation).
- 10 represents the width.
- 6 represents the height.
These dimensions are usually expressed in consistent units. For example, all three could be measured in centimeters (cm), meters (m), inches (in), or feet (ft). The absence of specified units implies a generic representation applicable to any consistent unit system. The key is maintaining consistency; mixing units (e.g., 2 meters x 10 centimeters x 6 inches) is incorrect and will lead to inaccurate calculations.
Calculating the Volume: Cubic Units and Spatial Capacity
A crucial application of these dimensions is calculating the volume of the rectangular prism. Volume represents the three-dimensional space enclosed within the object's boundaries and is measured in cubic units (e.g., cubic centimeters – cm³, cubic meters – m³, cubic inches – in³, cubic feet – ft³). To calculate the volume, we simply multiply the three dimensions:
Volume = Length x Width x Height = 2 x 10 x 6 = 120 cubic units
This means the rectangular prism described by 2 x 10 x 6 has a capacity of 120 cubic units. The specific unit (cm³, m³, etc.) depends entirely on the units used for the length, width, and height measurements. Understanding volume is critical in many applications, from estimating the capacity of containers to calculating the amount of material needed for construction projects.
Real-World Applications of 2 x 10 x 6 Dimensions
The dimensions 2 x 10 x 6, or variations thereof, appear in countless real-world scenarios. Here are a few examples:
-
Packaging and Shipping: Boxes with these dimensions are commonly used for shipping various goods. The exact dimensions might be slightly adjusted based on product size and packaging requirements, but the general proportions remain relevant. Understanding the volume helps optimize packing strategies and minimize shipping costs.
-
Construction and Engineering: These dimensions could represent the size of a structural component, such as a beam or a section of a wall. Accurate dimensional calculations are critical in construction to ensure stability and structural integrity.
-
Furniture Design and Manufacturing: The dimensions could reflect the size of a cabinet, a drawer, or a storage unit. Understanding volume is crucial in designing furniture that efficiently uses space and meets the needs of the user.
-
Aquariums and Fish Tanks: A tank with these proportions (after considering appropriate unit conversions) could be a suitable size for certain types of fish and aquatic plants. Understanding volume is vital for maintaining appropriate water levels and providing an adequate living space for aquatic life.
-
Gardening and Horticulture: A raised garden bed or a planter box with these dimensions could be used to cultivate various plants. Knowing the volume helps determine the amount of soil needed and facilitates efficient plant arrangement.
-
Data Storage and Server Racks: In a more abstract sense, these dimensions might represent the allocated space in a data center for servers or storage units. Efficient space utilization is paramount in data center management.
Exploring Variations and Scalability
The dimensions 2 x 10 x 6 are just one example of a rectangular prism. We can easily scale these dimensions up or down while maintaining the same proportions:
- Doubling the dimensions: 4 x 20 x 12 would result in a volume of 960 cubic units (8 times the original volume).
- Halving the dimensions: 1 x 5 x 3 would result in a volume of 15 cubic units (1/8 of the original volume).
This scalability demonstrates the flexibility of the concept and its adaptability to various contexts. The fundamental principle remains the same: multiplying the length, width, and height provides the volume.
Surface Area Calculations: Another Important Metric
While volume is crucial, understanding the surface area is equally important in many applications. Surface area is the total area of all the faces of the rectangular prism. For a prism with dimensions l, w, and h, the surface area is calculated as:
Surface Area = 2(lw + lh + wh)
For our 2 x 10 x 6 prism:
Surface Area = 2(2 x 10 + 2 x 6 + 10 x 6) = 2(20 + 12 + 60) = 2(92) = 184 square units
Surface area is critical when considering the amount of material needed for packaging, the amount of paint required to cover a surface, or the heat transfer from a surface.
Beyond Rectangular Prisms: Extending the Concept
While we've focused on rectangular prisms, the fundamental concept of multiplying dimensions to determine volume extends to other shapes:
-
Cubes: A cube is a special case of a rectangular prism where all three dimensions are equal. A 2 x 2 x 2 cube would have a volume of 8 cubic units.
-
Cylinders: The volume of a cylinder is calculated using πr²h, where 'r' is the radius and 'h' is the height. Here, the concept of multiplying dimensions is still relevant, albeit with a different formula.
-
Spheres: The volume of a sphere is (4/3)πr³, where 'r' is the radius. Again, understanding the relationship between dimensions and volume is fundamental.
Understanding these different shapes and their volume calculations broadens our understanding of spatial reasoning and problem-solving.
Frequently Asked Questions (FAQ)
Q: What are the units of measurement for 2 x 10 x 6?
A: The units are not specified in the expression "2 x 10 x 6." The dimensions could be in centimeters, meters, inches, feet, or any other consistent unit of length. It's crucial to specify the units when applying this to real-world problems.
Q: Can I use these dimensions for any type of object?
A: While the dimensions can represent many objects, they are primarily applicable to rectangular prisms or objects that can be approximated as such. For irregularly shaped objects, more complex volume calculations are needed.
Q: How do I determine the appropriate units for a specific application?
A: The appropriate units depend on the context of the problem. If you are dealing with a small object, centimeters or inches might be suitable. For larger objects, meters or feet might be more appropriate.
Q: What if one of the dimensions is zero?
A: If any of the dimensions is zero, the volume becomes zero. This represents a two-dimensional or one-dimensional object, depending on which dimensions are zero.
Conclusion: The Power of Simple Dimensions
The seemingly simple expression "2 x 10 x 6" encapsulates a wealth of information, extending far beyond a basic multiplication problem. Understanding these dimensions allows us to calculate volume, analyze spatial relationships, and apply these concepts to various real-world situations. Whether it's packaging goods, designing furniture, or constructing buildings, the ability to work with dimensions and volumes is a fundamental skill across numerous disciplines. This article has only scratched the surface; further exploration into geometry, mensuration, and related fields will reveal even more applications and deepen your understanding of the power of simple dimensions. Remember that consistent units are key to accurate calculations and successful problem-solving.
Latest Posts
Latest Posts
-
Biopsychosocial Model Of Addiction
Sep 19, 2025
-
270 Minutes To Hours
Sep 19, 2025
-
Description Of Irregular Bones
Sep 19, 2025
-
Convert Thou To Mm
Sep 19, 2025
-
Square Root Of 38
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2 10 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.