Square Root Of 38
renascent
Sep 19, 2025 · 6 min read
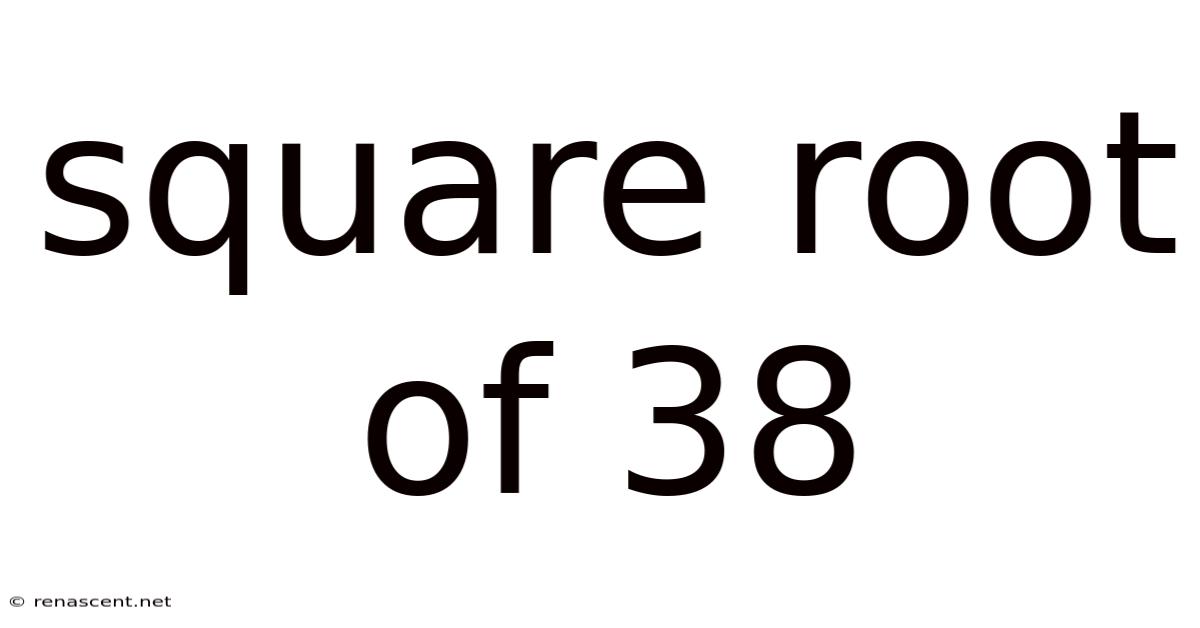
Table of Contents
Unveiling the Mysteries of the Square Root of 38: A Deep Dive into Calculation and Application
Finding the square root of 38 might seem like a simple mathematical task, but it opens a door to a fascinating world of numerical exploration, encompassing various methods of calculation, underlying mathematical principles, and practical applications across diverse fields. This article will delve into the intricacies of calculating the square root of 38, exploring both approximate and precise methods, and illustrating its relevance in real-world scenarios. We'll also address common questions and misconceptions surrounding this seemingly straightforward concept.
Understanding Square Roots: A Refresher
Before we embark on the journey of finding the square root of 38, let's solidify our understanding of the fundamental concept. The square root of a number is simply a value that, when multiplied by itself, equals the original number. For instance, the square root of 9 (√9) is 3 because 3 x 3 = 9. This concept applies to all non-negative real numbers. However, when dealing with numbers that are not perfect squares (like 38), we encounter a more complex scenario.
Methods for Calculating the Square Root of 38
Calculating the square root of 38 precisely is impossible without resorting to infinite decimal places. However, several methods allow us to obtain highly accurate approximations. Here are some of the most common approaches:
1. Using a Calculator: The Simplest Approach
The most straightforward way to find the square root of 38 is using a calculator. Simply input '√38' and the calculator will provide a decimal approximation, typically around 6.164414. This method offers quick results but doesn't provide insight into the underlying mathematical process.
2. Babylonian Method (or Heron's Method): An Iterative Approach
This ancient method is an iterative process that refines an initial guess until it converges to a satisfactory approximation. Here's how it works:
- Start with an initial guess: Let's choose 6 as our first guess, as 6 x 6 = 36, which is close to 38.
- Iterate: Use the formula: Next guess = (Previous guess + (Number / Previous guess)) / 2
- First iteration: (6 + (38 / 6)) / 2 ≈ 6.1667
- Second iteration: (6.1667 + (38 / 6.1667)) / 2 ≈ 6.164414
- Repeat: Continue this process until the difference between successive guesses is negligible. The more iterations you perform, the more accurate your approximation becomes.
3. Newton-Raphson Method: A More Advanced Iterative Technique
The Newton-Raphson method is a powerful iterative algorithm used for finding successively better approximations to the roots of a real-valued function. In the context of finding the square root of 38, we can apply this method by considering the function f(x) = x² - 38. The root of this function is the square root of 38. The iterative formula is:
x_(n+1) = x_n - f(x_n) / f'(x_n)
where f'(x_n) is the derivative of f(x), which in this case is 2x_n.
This method, while more complex than the Babylonian method, generally converges faster to a highly accurate approximation.
4. Long Division Method: A Manual Approach
While less efficient than iterative methods for finding the square root of 38, the long division method provides a deeper understanding of the underlying mathematical process. This method involves grouping digits in pairs, starting from the decimal point, and progressively finding digits of the square root. It's a lengthy process, and detailed explanation would require a separate dedicated article. However, it's worth noting that this method showcases the logic behind square root calculation without the use of calculators or advanced algorithms.
The Significance and Applications of √38
The square root of 38, while seemingly a simple mathematical concept, finds its application across a multitude of disciplines:
1. Geometry and Trigonometry: Calculating Lengths and Distances
In geometry, the square root often appears in calculations involving the Pythagorean theorem, which relates the lengths of the sides of a right-angled triangle. For instance, if we have a right-angled triangle with legs of length a and b, the hypotenuse (length c) is calculated as: c = √(a² + b²). Therefore, understanding square roots is crucial in determining lengths and distances in various geometric problems.
2. Physics and Engineering: Solving Equations and Modeling Systems
Square roots frequently arise in the solutions of many physical equations, often related to calculating speeds, velocities, accelerations, and forces. In engineering, understanding square roots is critical for designing structures, analyzing stresses, and determining various physical parameters. For example, calculating the period of a simple pendulum involves the square root of its length.
3. Statistics and Data Analysis: Standard Deviation and Variance
The standard deviation, a key measure of data dispersion, often involves calculating the square root of the variance. Understanding square roots is essential for accurately interpreting and analyzing statistical data.
4. Computer Graphics and Game Development: Vector Calculations
In computer graphics and game development, vectors are used extensively to represent positions, directions, and other properties of objects. Vector calculations often involve square roots to determine magnitudes or distances between points in space.
5. Financial Modeling: Calculating Returns and Risk
In finance, standard deviation is used to measure the risk associated with investment portfolios. This requires calculating the square root of the variance of investment returns, demonstrating the importance of square roots in financial modeling and risk management.
Addressing Common Questions and Misconceptions
Let's address some frequently encountered questions and misconceptions regarding square roots:
Q: Is there a single, precise value for √38?
A: No, the precise value of √38 cannot be expressed as a finite decimal. It's an irrational number, meaning its decimal representation continues infinitely without repeating. Calculators and other methods provide approximations to a certain level of precision.
Q: Why is it important to learn different methods for calculating square roots?
A: Understanding multiple methods provides a deeper appreciation of the mathematical principles behind square root calculation. While calculators provide quick answers, learning methods like the Babylonian method or long division method enhances mathematical comprehension and problem-solving skills.
Q: Can negative numbers have square roots?
A: Within the realm of real numbers, negative numbers do not have square roots. However, in the complex number system, the square root of a negative number is defined using the imaginary unit 'i', where i² = -1.
Q: What is the significance of irrational numbers like √38?
A: Irrational numbers, like √38, are essential components of the number system, demonstrating the richness and complexity of mathematics. They frequently appear in various mathematical, scientific, and engineering applications, highlighting their importance in accurately modeling and representing real-world phenomena.
Conclusion: The Beauty of Approximation and Precision
The quest to find the square root of 38 unveils the fascinating interplay between approximation and precision in mathematics. While a perfectly precise answer remains elusive within the realm of real numbers, various methods offer accurate approximations suitable for practical applications. Understanding these methods and appreciating the broader significance of square roots across different fields enhances our comprehension of mathematics and its profound impact on our world. From the ancient Babylonian method to the advanced Newton-Raphson technique, each approach offers a unique perspective on this fundamental concept, highlighting the beauty and power of mathematical exploration. The journey of understanding √38 serves as a testament to the enduring relevance and ongoing evolution of mathematical knowledge.
Latest Posts
Latest Posts
-
132 Kg To Lbs
Sep 19, 2025
-
What Rhymes With Tree
Sep 19, 2025
-
5 Divided By 23
Sep 19, 2025
-
Viktor Krum And Hermione
Sep 19, 2025
-
1742 Divided By 2
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 38 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.