10 Divided By 2
renascent
Sep 16, 2025 · 5 min read
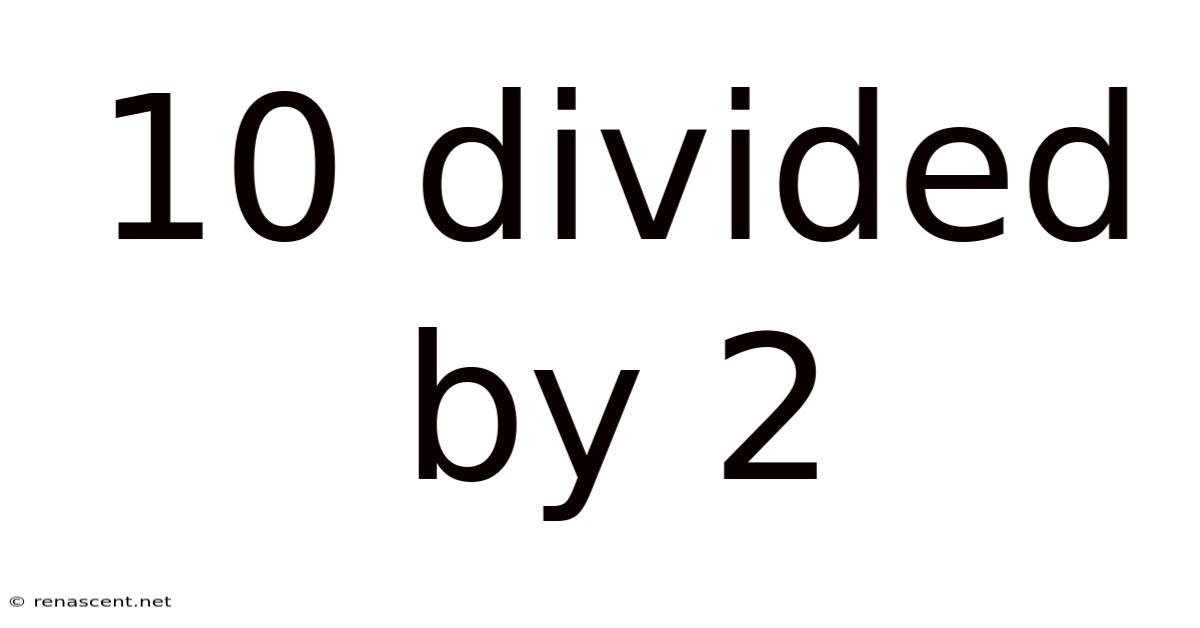
Table of Contents
10 Divided by 2: A Deep Dive into Simple Division
The seemingly simple calculation of 10 divided by 2 – often represented as 10 ÷ 2 or 10/2 – might appear trivial at first glance. However, this fundamental arithmetic operation provides a gateway to understanding broader mathematical concepts, from basic division principles to more complex applications in algebra, calculus, and even programming. This article will explore 10 divided by 2 in detail, examining its solution, its underlying principles, and its significance within the larger framework of mathematics. We'll delve into different approaches to solving this problem, explore its real-world applications, and answer frequently asked questions to provide a comprehensive understanding.
Understanding Division: The Foundation
Before diving into the specifics of 10 ÷ 2, let's establish a firm understanding of what division actually represents. Division is essentially the opposite of multiplication. Multiplication combines equal groups to find a total, while division breaks a total into equal groups to find the size of each group or the number of groups.
In the context of 10 ÷ 2, we're asking: "If we have 10 items and want to divide them into 2 equal groups, how many items will be in each group?" This question forms the core of the division problem.
Solving 10 Divided by 2: The Simple Approach
The solution to 10 ÷ 2 is straightforward: 5. This can be easily visualized. Imagine 10 apples; if you divide them into two equal piles, each pile will contain 5 apples. This simple visual representation highlights the core concept of equal sharing that underpins division.
This simple solution can also be derived through the inverse operation of multiplication. We are looking for a number that, when multiplied by 2, equals 10. That number is 5 (2 x 5 = 10).
Different Approaches to Division: Exploring Methodologies
While the solution to 10 ÷ 2 is readily apparent, exploring different approaches to division reinforces understanding and prepares us for more complex problems. Here are some methodologies:
-
Repeated Subtraction: We can repeatedly subtract 2 from 10 until we reach zero. The number of times we subtract 2 is the answer. 10 - 2 = 8; 8 - 2 = 6; 6 - 2 = 4; 4 - 2 = 2; 2 - 2 = 0. We subtracted 2 five times, confirming the answer is 5. This method is particularly helpful in understanding the concept of division as repeated subtraction.
-
Long Division: While not strictly necessary for such a simple problem, long division provides a systematic approach applicable to more complex divisions. For 10 ÷ 2, the process would look like this:
2 | 10 -10 0The quotient (the answer) is 5. This method becomes crucial when dealing with larger numbers and remainders.
-
Fractions: Division can also be expressed as a fraction. 10 ÷ 2 is equivalent to the fraction 10/2. Simplifying this fraction gives us 5/1, or simply 5. This connection between division and fractions is essential for understanding rational numbers.
Real-World Applications: Division in Everyday Life
Division is not just an abstract mathematical concept; it’s a tool used extensively in everyday life. Here are some real-world examples where understanding 10 ÷ 2, and division in general, proves valuable:
-
Sharing Equally: Dividing a pizza amongst two friends, splitting a bill between two people, or distributing 10 candies equally between two children all involve the fundamental principle of division.
-
Measurement and Conversions: Converting units often requires division. For instance, if you have 10 meters of fabric and need to cut it into 2-meter pieces, you'll use division to determine the number of pieces (10 ÷ 2 = 5).
-
Pricing and Budgeting: Calculating the cost per item, determining the unit price, or dividing a budget across different categories all involve the application of division.
-
Averages: Calculating the average of a set of numbers often involves division. For example, to find the average of two numbers, you would add them and then divide by 2.
10 Divided by 2 in Advanced Mathematics: Beyond the Basics
While seemingly simple, the concept of 10 divided by 2 underpins more complex mathematical operations and theories.
-
Algebra: Division is crucial in solving algebraic equations. For example, to solve the equation 2x = 10, we divide both sides by 2 to isolate x, resulting in x = 5.
-
Calculus: Division is used extensively in calculus, particularly in differentiation and integration, where it plays a critical role in finding rates of change and areas under curves.
-
Programming: Division is a fundamental arithmetic operation in computer programming, used in various algorithms and calculations. Programming languages use the division operator (often "/") to perform this function.
Frequently Asked Questions (FAQs)
Q: What is the remainder when 10 is divided by 2?
A: There is no remainder when 10 is divided by 2. The division is exact.
Q: Can 10 be divided by other numbers besides 2?
A: Yes, 10 can be divided by 1, 5, and 10. These numbers are all factors of 10.
Q: What happens if we try to divide 10 by 0?
A: Dividing by zero is undefined in mathematics. It's a concept that leads to inconsistencies and is therefore not allowed.
Q: How does division relate to fractions?
A: Division and fractions are intimately related. The expression "a divided by b" is equivalent to the fraction a/b.
Q: Is there a difference between 10 ÷ 2 and 2 ÷ 10?
A: Yes, there's a significant difference. 10 ÷ 2 = 5, while 2 ÷ 10 = 0.2 (or 1/5). The order of the numbers in division significantly impacts the result.
Conclusion: The Significance of Simplicity
While the calculation of 10 divided by 2 may seem elementary, its significance extends far beyond a simple arithmetic problem. Understanding this fundamental operation provides a bedrock for grasping more complex mathematical concepts, problem-solving skills, and real-world applications across various fields. The seemingly simple act of division lays the foundation for a deeper understanding of numbers and their relationships, paving the way for more advanced mathematical explorations. Through different approaches and real-world examples, we’ve demonstrated that the seemingly trivial calculation of 10 ÷ 2 holds a wealth of mathematical significance and practical utility. This seemingly simple calculation is a cornerstone of mathematical understanding and practical application.
Latest Posts
Latest Posts
-
200 C En F
Sep 16, 2025
-
68 F In Celsius
Sep 16, 2025
-
Reliability Validity And Accuracy
Sep 16, 2025
-
Operation Phoenix Vietnam War
Sep 16, 2025
-
What Do Dn Mean
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 10 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.