10 Percent Of 1000
renascent
Sep 19, 2025 · 5 min read
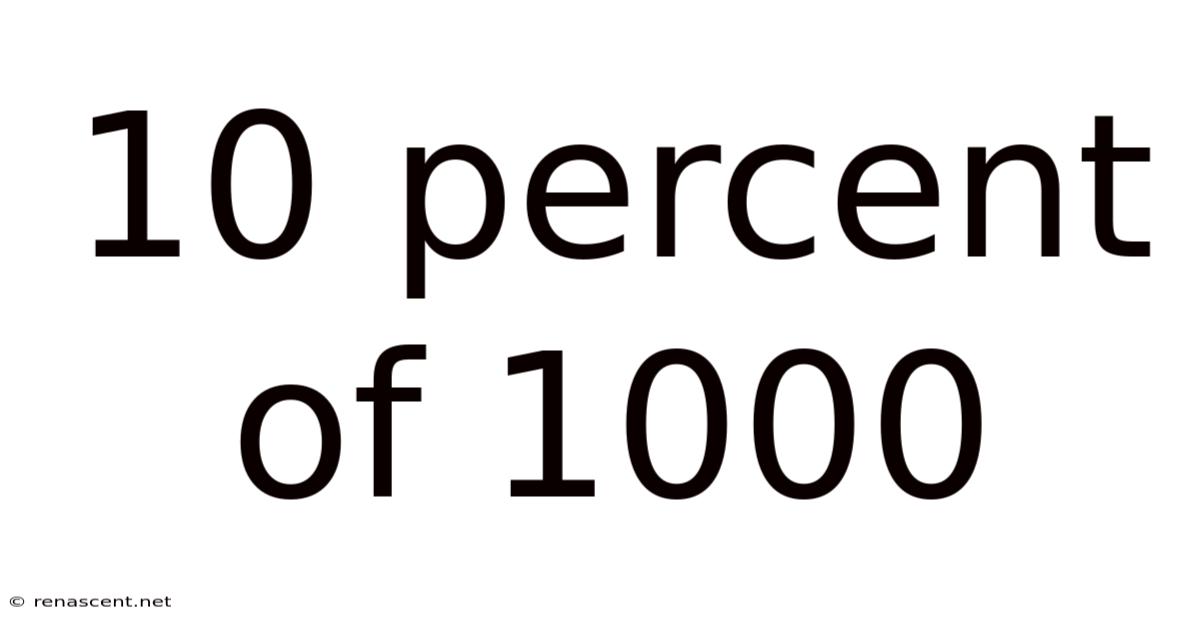
Table of Contents
Decoding 10 Percent of 1000: A Comprehensive Guide to Percentages
Finding 10 percent of 1000 might seem like a simple calculation, a piece of cake even. But understanding percentages extends far beyond this basic example. It's a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating sales tax and discounts to understanding financial reports and statistical data. This article dives deep into the meaning of "10 percent of 1000," exploring the calculation itself, its broader implications, and practical applications across various fields. We'll also tackle some common percentage-related questions and misconceptions.
Understanding Percentages: The Basics
Before we tackle the specific problem of 10 percent of 1000, let's solidify our understanding of percentages. The word "percent" literally means "out of one hundred." A percentage represents a fraction or proportion out of 100. For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is crucial for navigating percentage calculations.
Calculating 10 Percent of 1000
The calculation itself is straightforward:
-
Method 1: Using the Decimal Equivalent: The easiest method involves converting the percentage to its decimal equivalent. 10% is equal to 0.10 (or simply 0.1). To find 10% of 1000, we multiply 1000 by 0.1:
1000 x 0.1 = 100
-
Method 2: Using Fractions: We can express 10% as a fraction: 10/100. This simplifies to 1/10. To find 10% of 1000, we multiply 1000 by 1/10:
1000 x (1/10) = 100
Therefore, 10 percent of 1000 is 100.
Beyond the Calculation: Real-World Applications
While the calculation itself is simple, the concept of percentages has extensive applications across various fields:
-
Finance: Percentages are fundamental to finance. Interest rates on loans and savings accounts, investment returns, inflation rates, and tax calculations all rely on percentage calculations. Understanding percentages is essential for making informed financial decisions. For example, if you invest $1000 and earn a 10% return, you'll have an additional $100.
-
Retail and Sales: Discounts, sales tax, and markups are all expressed as percentages. If a store offers a 10% discount on a $1000 item, you'll save $100, paying only $900. Conversely, if a store marks up an item by 10%, the final price will be $1100.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions and probabilities. Survey results, population demographics, and scientific data often use percentages to summarize and present information in a readily understandable format. For instance, if a survey shows that 10% of respondents prefer a particular brand, this indicates that out of 1000 respondents, 100 preferred that brand.
-
Science and Engineering: Percentages are used in many scientific and engineering contexts, including expressing concentrations, efficiencies, and error margins. For example, a solution might contain 10% salt by weight, meaning 100 grams of salt in 1000 grams of solution.
-
Everyday Life: Percentages appear frequently in everyday contexts, from tipping in restaurants (e.g., a 10% tip on a $100 meal) to understanding nutritional information on food labels (e.g., the percentage of daily recommended value of vitamins).
Working with Different Percentages: A Step-by-Step Guide
Let's extend our understanding beyond 10%. Here's a step-by-step guide for calculating any percentage of 1000:
-
Convert the percentage to a decimal: Divide the percentage by 100. For example, 25% becomes 0.25, 5% becomes 0.05, and 150% becomes 1.5.
-
Multiply the decimal by 1000: This gives you the result.
Examples:
- 25% of 1000: 0.25 x 1000 = 250
- 5% of 1000: 0.05 x 1000 = 50
- 150% of 1000: 1.5 x 1000 = 1500
Calculating the Percentage: Finding the Percentage One Number Represents of Another
The reverse calculation—finding what percentage one number represents of another—is equally important. Suppose you sold 100 items out of 1000. What percentage of your inventory did you sell?
-
Divide the smaller number by the larger number: 100 / 1000 = 0.1
-
Multiply the result by 100 to express it as a percentage: 0.1 x 100 = 10%
Therefore, you sold 10% of your inventory.
Common Percentage Mistakes and Misconceptions
Several common mistakes can arise when working with percentages:
-
Confusing percentage change with absolute change: A 10% increase from 1000 is 100, resulting in 1100. However, a 10% decrease from 1100 is 110, resulting in 990, not 1000. The starting point is crucial.
-
Incorrectly adding or subtracting percentages: You cannot simply add or subtract percentages directly without considering the base amount. For instance, a 10% increase followed by a 10% decrease does not result in the original value.
-
Misinterpreting percentage points: Percentage points represent the difference between two percentages, not a percentage change. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage itself.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage of a number other than 1000? A: Follow the same steps outlined above. Convert the percentage to a decimal and multiply it by the number you're working with.
-
Q: What if the percentage is greater than 100%? A: This means the result will be larger than the original number. For example, 150% of 1000 is 1500.
-
Q: Are there any online calculators for percentages? A: Yes, many online calculators are readily available to help you perform percentage calculations quickly and accurately.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a fundamental life skill. While finding 10 percent of 1000 is a simple calculation, the underlying concept has broad implications across various fields. Mastering percentage calculations equips you with the tools to navigate financial decisions, interpret data, and tackle everyday problems more effectively. From analyzing sales figures to understanding financial reports or simply calculating discounts, a solid grasp of percentages unlocks a deeper comprehension of the numerical world around us. By understanding not just the calculation but also the broader context and potential pitfalls, you'll be well-equipped to confidently handle percentages in any situation.
Latest Posts
Latest Posts
-
The Underland Chronicles Series
Sep 20, 2025
-
70 Divided By 12
Sep 20, 2025
-
6 20 Simplified Fraction
Sep 20, 2025
-
55 5 Kg To Lbs
Sep 20, 2025
-
Example Of Physical Contamination
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 10 Percent Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.