10 X 7 8
renascent
Sep 22, 2025 · 6 min read
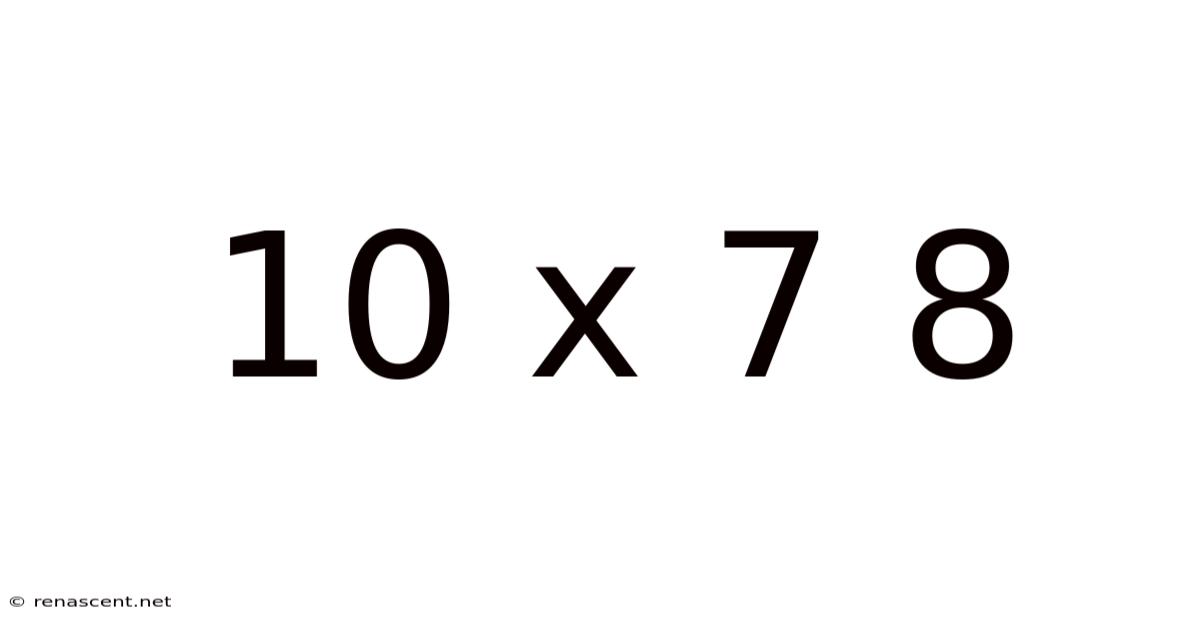
Table of Contents
Decoding "10 x 7 8": Exploring the Multifaceted Interpretations of a Seemingly Simple Expression
The expression "10 x 7 8" might initially appear straightforward, a simple multiplication problem. However, a deeper dive reveals a fascinating ambiguity, sparking discussions across multiple disciplines, from basic arithmetic to more complex areas like programming logic and even philosophical interpretations of representation. This article delves into the various interpretations of "10 x 7 8," examining its mathematical implications, potential programming contexts, and the broader implications of ambiguity in communication.
Understanding the Basic Mathematical Interpretation
At its most fundamental level, "10 x 7 8" presents a challenge in operator precedence. Standard mathematical notation dictates that multiplication takes precedence over addition or subtraction. However, the absence of explicit operators between the numbers leaves room for different interpretations.
-
Interpretation 1: Sequential Multiplication: One could interpret this as a series of multiplications: (10 x 7) x 8. Following the order of operations, this yields 70 x 8 = 560. This interpretation relies on the implicit assumption that each number is multiplied sequentially.
-
Interpretation 2: Concatenation and Multiplication: Another possible interpretation involves treating the numbers as concatenated strings before multiplication. This would mean treating "10 x 7 8" as 1078, a number formed by joining the digits. However, the ‘x’ symbol would still need a clear definition. If ‘x’ represents multiplication by 10, then the outcome would be 10780. If we assume that it is a standard multiplication sign that is separated from the numbers, then 1078 would require further clarification in terms of what it is multiplied by to yield a final answer. Ultimately, this interpretation highlights the importance of precise notation.
-
Interpretation 3: Implicit Addition/Concatenation: We could also imagine an interpretation where the expression is implicitly suggesting a summation or concatenation with an implied multiplication: (10 + 7) * 8 or (10 + 7 + 8). In these scenarios, we'd obtain: (17 * 8) = 136, and (10 + 7 + 8) = 25 respectively. Again, such interpretations underscore the dangers of ambiguous notation.
The ambiguity underscores the critical role of clear and unambiguous notation in mathematics. Without parentheses or clearly defined operators, the meaning becomes uncertain, leading to multiple possible answers. This is a vital lesson in mathematical communication – clarity prevents errors and misunderstandings.
Exploring Programming Context: Operator Precedence and Data Types
In programming, the interpretation of "10 x 7 8" can also vary depending on the programming language and how the expression is coded.
-
Standard Programming Languages (C++, Java, Python): In most standard programming languages, the expression would likely generate a syntax error unless operators are explicitly defined. These languages require explicit operators (+, -, *, /) between operands. An attempt to directly interpret "10 x 7 8" would usually lead to a compiler or interpreter error indicating that the expression is invalid.
-
Custom Functions or Operators: A programmer could define custom functions or operators to handle this expression in a specific way. For instance, a function could be created that takes a string as input, parses it, and performs operations according to a predefined rule. This allows for flexibility but requires the code to explicitly define the desired behavior.
-
String Manipulation: If the expression is treated as a string, programming languages offer methods to manipulate strings. One could extract the numbers from the string and then perform mathematical operations based on a chosen interpretation. However, this approach needs careful consideration of string parsing and error handling.
The programming context emphasizes the importance of explicit code and the need for well-defined syntax. Unlike mathematical notation where some ambiguity can be tolerated (with careful interpretation), programming languages demand precision to avoid errors and ensure consistent behavior.
The Philosophical Interpretation: Ambiguity and Representation
Beyond mathematics and programming, the expression "10 x 7 8" offers a compelling philosophical perspective on the nature of representation and interpretation.
-
The Role of Context: The meaning of "10 x 7 8" is heavily dependent on the context in which it appears. Its meaning is not inherent in the string of characters itself, but is assigned by the interpreter based on their understanding of mathematical rules, programming conventions, or any other relevant framework.
-
The Limits of Symbolism: The example illustrates the limitations of symbolic representation. Symbols, while powerful tools for communication, are only meaningful when there is a shared understanding of their interpretation. The ambiguity of "10 x 7 8" highlights the potential for miscommunication when there is a lack of clarity in the use of symbols.
-
Interpretation as a Creative Act: We could even argue that interpreting "10 x 7 8" is a creative act. The lack of explicit rules encourages the interpreter to actively construct a meaning, drawing upon their prior knowledge and assumptions. This resonates with broader philosophical discussions of interpretation and the role of the observer in assigning meaning.
Practical Applications and Problem-Solving Approaches
While "10 x 7 8" may seem like an abstract exercise, its ambiguity can be used to explore broader problem-solving strategies.
-
Developing Clear Communication Skills: The expression is a stark reminder of the importance of clear and unambiguous communication in all fields. The potential for misinterpretation underscores the need for precision in conveying information, whether in mathematical contexts or everyday life.
-
Developing Critical Thinking Skills: Analyzing the multiple interpretations of "10 x 7 8" fosters critical thinking skills. It encourages individuals to question assumptions, explore multiple perspectives, and evaluate different interpretations to arrive at a meaningful solution.
-
Enhancing Mathematical Reasoning: By systematically exploring different interpretations, and justifying why certain interpretations are more plausible based on mathematical conventions, one enhances their understanding of operator precedence and mathematical notation.
-
Promoting Programming Logic: The need to handle this expression within a programming context highlights the importance of considering various data types, operator precedence rules in programming, and the need for robust error handling.
Frequently Asked Questions (FAQ)
-
Q: What is the correct answer to "10 x 7 8"? A: There is no single "correct" answer without additional context or clarification. The expression is inherently ambiguous.
-
Q: Why is this expression ambiguous? A: It's ambiguous because it lacks clearly defined operators between the numbers. Without parentheses or explicit symbols specifying the order of operations, multiple interpretations are possible.
-
Q: How can I avoid ambiguity in mathematical expressions? A: Use parentheses to explicitly define the order of operations. Be consistent in your notation and ensure that your operators are clearly defined.
-
Q: Is this a real-world problem? A: While "10 x 7 8" is a simplified example, the issue of ambiguous notation and the need for clear communication is a real-world problem in many fields, particularly in mathematics, programming, and engineering.
Conclusion: The Power of Precision and Context
The seemingly simple expression "10 x 7 8" serves as a potent reminder of the importance of precision, context, and unambiguous communication. Its multiple interpretations highlight the critical role of clear notation in mathematics and programming, and it offers a fascinating glimpse into the philosophical considerations of representation and interpretation. While there's no single "correct" answer without further clarification, the process of analyzing its various interpretations reveals a wealth of insights across multiple disciplines, underscoring the significance of careful thought and communication in all endeavors. The ambiguity of this expression is not a flaw, but rather an opportunity for deeper understanding and learning.
Latest Posts
Latest Posts
-
150 Mins In Hours
Sep 22, 2025
-
Does Chlorine Reduce Ph
Sep 22, 2025
-
360 Divided By 3
Sep 22, 2025
-
Copper Chloride Chemical Formula
Sep 22, 2025
-
Nitrogen And Hydrogen Gas
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 10 X 7 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.