1000 Divided By 10
renascent
Sep 14, 2025 · 6 min read
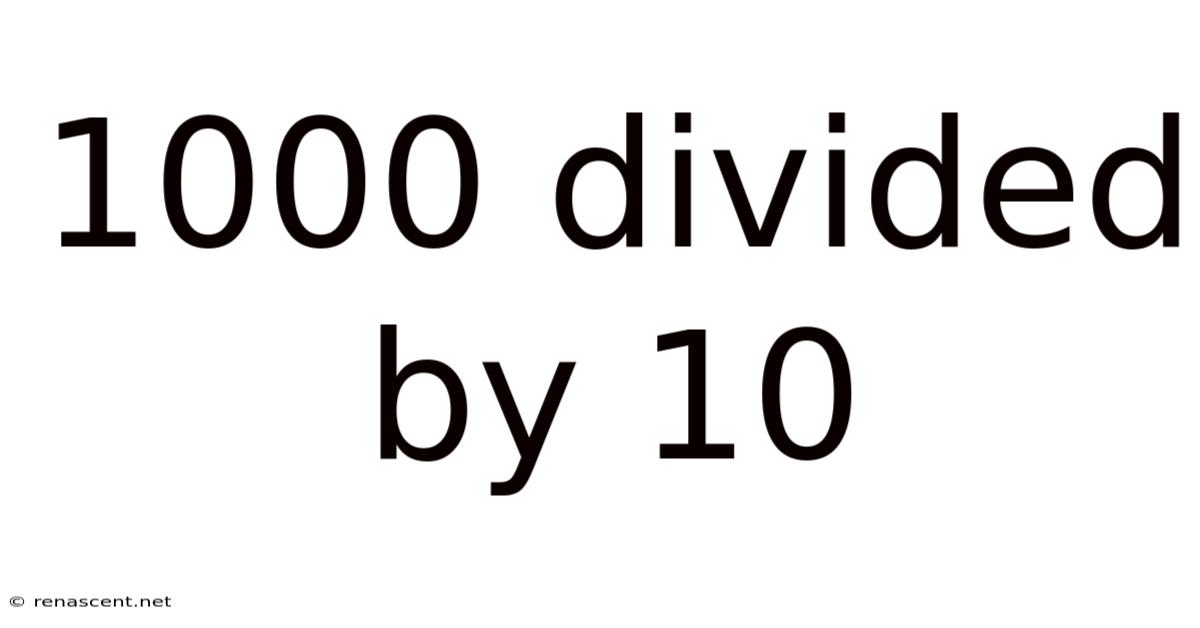
Table of Contents
1000 Divided by 10: A Deep Dive into Simple Division and its Real-World Applications
This article explores the seemingly simple calculation of 1000 divided by 10, delving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and broader implications within arithmetic, algebra, and beyond. Understanding this fundamental operation is crucial for grasping more complex mathematical concepts and solving real-world problems. We'll explore different methods of solving this problem, discuss its relevance in various fields, and even touch upon the historical context of division.
Introduction: The Foundation of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts or groups. The problem "1000 divided by 10" can be expressed mathematically as 1000 ÷ 10 or 1000/10. This essentially asks: "How many times does 10 fit into 1000?" The answer, as we'll demonstrate in various ways, is 100. But the journey to understanding this answer is far more enriching than simply stating the result.
Method 1: Direct Calculation
The most straightforward method to solve 1000 ÷ 10 is direct calculation. Since we're dealing with multiples of 10, the process is simplified. We can visualize this by thinking of 1000 as ten hundreds (10 x 100). Therefore, dividing 1000 by 10 is the same as asking how many hundreds are in 1000, which is 100.
Alternatively, we can use the basic principle of division: If we repeatedly subtract the divisor (10) from the dividend (1000) until we reach zero, the number of times we subtract represents the quotient. While impractical for larger numbers, this method visually reinforces the concept of division.
Method 2: Long Division
Long division is a more formal method, especially useful for more complex division problems. Though overkill for 1000 ÷ 10, it demonstrates a systematic approach applicable to more challenging calculations.
- Set up the long division problem: 10 | 1000
- Divide the first digit of the dividend (1) by the divisor (10). Since 1 is smaller than 10, we consider the first two digits (10).
- 10 divided by 10 is 1. Write 1 above the line.
- Multiply the quotient (1) by the divisor (10): 1 x 10 = 10.
- Subtract the result (10) from the first two digits of the dividend (10): 10 - 10 = 0.
- Bring down the next digit (0).
- Repeat steps 2-6 until all digits are processed. The remaining zeros will consistently yield a quotient of 0, leaving us with a final answer of 100.
Method 3: Using Exponents and Scientific Notation
Understanding exponents and scientific notation provides another perspective. We can express 1000 as 10³, meaning 10 multiplied by itself three times (10 x 10 x 10). The problem then becomes (10³)/10. Using the rules of exponents, we subtract the exponent of the denominator from the exponent of the numerator: 10^(3-1) = 10². 10² is 10 x 10 = 100. This method highlights the relationship between powers of 10 and division.
Real-World Applications: Where 1000/10 Matters
The seemingly simple calculation of 1000 ÷ 10 has surprisingly widespread applications:
-
Resource Allocation: Imagine dividing 1000 liters of water equally among 10 containers. The answer, 100 liters per container, is directly derived from 1000 ÷ 10. This is applicable to numerous resource management scenarios, from industrial production to household budgeting.
-
Financial Calculations: Distributing a $1000 bonus equally among 10 employees involves the same calculation, resulting in $100 per employee. This extends to various financial calculations involving profit sharing, investment returns, or loan repayments.
-
Measurement Conversion: Converting units often involves division. For example, if you have 1000 centimeters and need to find out how many meters that is (since 1 meter equals 100 centimeters), you would calculate 1000 ÷ 100 = 10 meters. While not directly 1000/10, it illustrates the fundamental concept in a different context.
-
Data Analysis: In statistics and data science, dividing a large dataset into smaller, manageable chunks for analysis is common. For instance, splitting 1000 data points into 10 groups for analysis would involve this basic division.
-
Engineering and Construction: Dividing materials equally among multiple projects or construction sites frequently uses this type of calculation. For example, splitting 1000 bricks into 10 piles for different parts of a building.
-
Everyday Life: Dividing tasks, sharing resources amongst family members, or splitting bills are just a few everyday examples where this simple division principle comes into play.
Extending the Concept: Beyond Simple Division
Understanding 1000 ÷ 10 lays a solid foundation for more complex mathematical operations:
-
Algebra: The concept extends to algebraic equations. Solving for 'x' in the equation 10x = 1000 involves the same division principle: x = 1000 ÷ 10 = 100.
-
Calculus: The concept of dividing infinitesimally small quantities is fundamental to calculus, though the calculations become significantly more intricate.
-
Statistics and Probability: Dividing totals by the number of data points is a cornerstone of statistical analysis, providing averages and other descriptive statistics.
-
Computer Science: Division is a fundamental operation in computer programming and algorithms. Many complex calculations rely on the efficient execution of basic arithmetic operations like division.
Historical Context: The Evolution of Division
The concept of division has ancient roots, with evidence suggesting its use in various early civilizations. While the notation and methods have evolved, the underlying principle of splitting a quantity into equal parts has remained constant throughout history. Early civilizations used concrete methods like distributing objects physically to represent division, gradually developing more abstract and symbolic representations.
Frequently Asked Questions (FAQ)
-
What is the remainder when 1000 is divided by 10? There is no remainder; 10 divides evenly into 1000.
-
How do I calculate 1000 divided by 10 using a calculator? Simply input "1000 ÷ 10" or "1000/10" into the calculator and press the equals button.
-
Are there other ways to express 1000 divided by 10? Yes, it can be written as 1000 ÷ 10, 1000/10, or even as a fraction 1000/10. All represent the same mathematical operation.
-
What if I divide 1000 by a number other than 10? The process remains the same; you would use the same methods (direct calculation, long division, etc.) to find the quotient.
Conclusion: The Significance of Simplicity
While 1000 divided by 10 might seem trivial, its significance lies in its fundamental nature. It represents a building block upon which more complex mathematical concepts are constructed. Understanding this simple operation not only provides a practical tool for solving everyday problems but also strengthens one's grasp of fundamental mathematical principles, paving the way for tackling more advanced challenges in various fields. Mastering the basics is crucial for success in mathematics and its numerous applications in the world around us. The seemingly simple answer of 100 unlocks a deeper understanding of the power and versatility of division in mathematics and its real-world impact.
Latest Posts
Latest Posts
-
46 Kilo In Stone
Sep 14, 2025
-
1 2 Of 3 1 2
Sep 14, 2025
-
Mollie From Animal Farm
Sep 14, 2025
-
207 Lbs To Kg
Sep 14, 2025
-
1500 Kg To Pounds
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1000 Divided By 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.