12 And 5 Lcm
renascent
Sep 24, 2025 · 6 min read
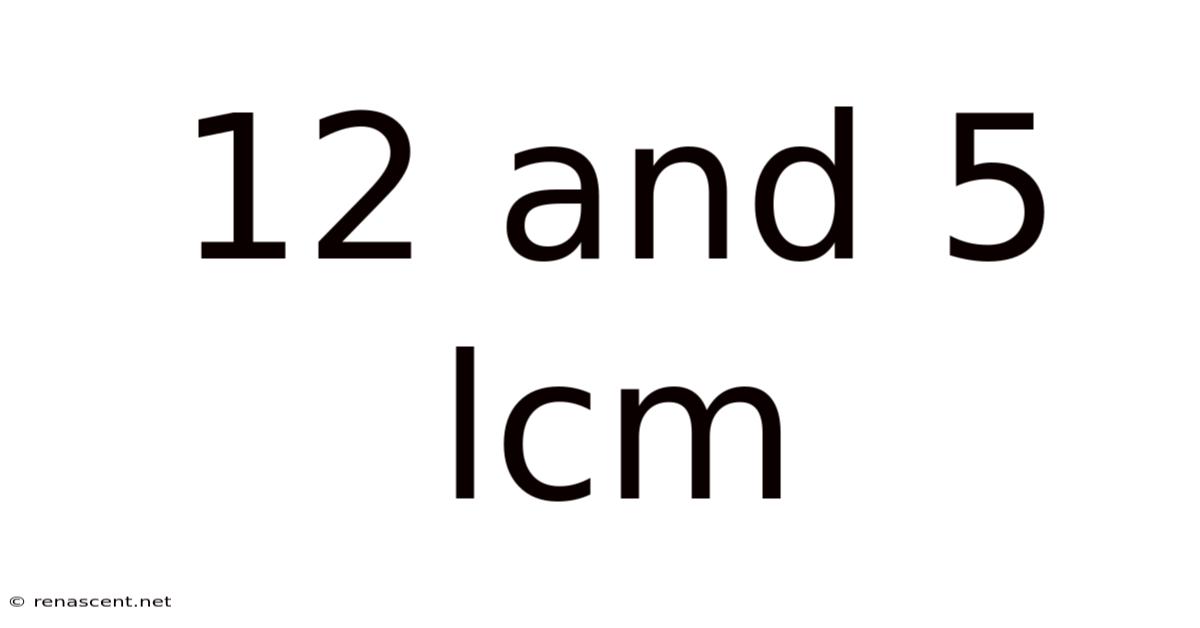
Table of Contents
Understanding the Least Common Multiple (LCM): A Deep Dive into Finding the LCM of 12 and 5
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex algebraic equations. This comprehensive guide will delve into the intricacies of calculating the LCM, specifically focusing on finding the LCM of 12 and 5. We'll explore multiple methods, explain the underlying principles, and address frequently asked questions, ensuring a thorough understanding for learners of all levels. Understanding LCMs is key to mastering fractions, ratios, and more advanced mathematical concepts.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly. For example, the multiples of 2 are 2, 4, 6, 8, 10, 12… and the multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
This concept extends to any number of integers. Finding the LCM is crucial in various mathematical operations, especially when working with fractions and simplifying expressions. Understanding the LCM helps in finding a common denominator for adding or subtracting fractions, simplifying ratios, and solving problems involving periodic events.
Methods for Finding the LCM of 12 and 5
There are several effective methods to determine the LCM of two numbers, such as 12 and 5. Let's explore the most common ones:
1. Listing Multiples Method:
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84…
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, …
By comparing the lists, we see that the smallest number present in both lists is 60. Therefore, the LCM of 12 and 5 is 60. This method is simple to visualize but can become cumbersome for larger numbers.
2. Prime Factorization Method:
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. Prime factors are prime numbers that multiply together to give the original number.
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 5: 5 (5 is a prime number)
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together.
In this case, the prime factors are 2, 3, and 5. The highest power of 2 is 2², the highest power of 3 is 3¹, and the highest power of 5 is 5¹. Therefore, the LCM is:
2² x 3 x 5 = 4 x 3 x 5 = 60
This method is more systematic and efficient, especially when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method:
The LCM and the greatest common divisor (GCD), also known as the highest common factor (HCF), are closely related. The GCD is the largest number that divides both numbers evenly. We can use the following formula to relate LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
First, let's find the GCD of 12 and 5 using the Euclidean algorithm:
12 = 5 x 2 + 2 5 = 2 x 2 + 1 2 = 1 x 2 + 0
The last non-zero remainder is the GCD, which is 1.
Now, using the formula:
LCM(12, 5) x GCD(12, 5) = 12 x 5 LCM(12, 5) x 1 = 60 LCM(12, 5) = 60
This method is particularly useful when the GCD is easily calculated, often using the Euclidean algorithm.
Why is the LCM Important?
Understanding and applying the LCM concept is essential in various mathematical contexts:
-
Adding and Subtracting Fractions: To add or subtract fractions with different denominators, we need to find a common denominator, which is typically the LCM of the denominators. This ensures we are working with equivalent fractions that can be added or subtracted directly.
-
Simplifying Fractions: The LCM helps in simplifying fractions to their lowest terms. By dividing both the numerator and the denominator by their GCD, we obtain the simplest form of the fraction.
-
Solving Ratio Problems: Ratios often involve finding equivalent ratios with a common denominator. The LCM is instrumental in achieving this.
-
Cyclic Events: The LCM is useful in problems involving cyclical events, such as determining when two events will occur simultaneously again. For instance, if event A happens every 12 days and event B every 5 days, the LCM (60) tells us when both events will coincide again.
-
Modular Arithmetic: The LCM is fundamental in solving congruences and other problems within modular arithmetic.
Further Exploration: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly efficient in this case. For example, let's find the LCM of 12, 5, and 15.
- Prime factorization of 12: 2² x 3
- Prime factorization of 5: 5
- Prime factorization of 15: 3 x 5
The highest power of each prime factor is: 2², 3¹, and 5¹. Therefore, the LCM(12, 5, 15) = 2² x 3 x 5 = 60.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The LCM (Least Common Multiple) is the smallest number that is a multiple of both (or all) given numbers. The GCD (Greatest Common Divisor), also known as the highest common factor (HCF), is the largest number that divides both (or all) given numbers evenly. They are inversely related, as shown in the formula: LCM(a,b) * GCD(a,b) = a * b
Q2: Can the LCM of two numbers be one of the numbers?
A2: Yes, if one number is a multiple of the other, the LCM will be the larger number. For example, the LCM of 6 and 12 is 12.
Q3: Is there a limit to the number of integers for which we can find the LCM?
A3: No, the concept of LCM extends to any number of integers. The prime factorization method is particularly useful for finding the LCM of many numbers.
Q4: How can I check if my calculated LCM is correct?
A4: Verify that the calculated LCM is divisible by all the original numbers. You can also use online LCM calculators to cross-check your results. Furthermore, you can use the relationship between LCM and GCD as a verification method.
Q5: Are there any real-world applications of LCM besides mathematical problems?
A5: Yes, LCM has practical applications in scheduling tasks, aligning cyclical events (like planetary orbits), and various engineering and programming problems involving timing and synchronization.
Conclusion
Finding the least common multiple (LCM) is a crucial skill in mathematics with broad applications across various fields. We've explored multiple methods for finding the LCM, specifically focusing on the LCM of 12 and 5, which is 60. Understanding the different methods, from listing multiples to using prime factorization and the GCD method, allows for efficient calculation depending on the numbers involved. This comprehensive guide provides a solid foundation for understanding and applying the LCM concept in various mathematical contexts and beyond. Remember to practice regularly to master this fundamental mathematical concept and its practical applications. The more you work with LCM problems, the more intuitive and efficient your calculations will become.
Latest Posts
Latest Posts
-
35 40 As Percent
Sep 24, 2025
-
Square Root Of 164
Sep 24, 2025
-
382 Divided By 5
Sep 24, 2025
-
What Does Sunshine Symbolize
Sep 24, 2025
-
Square Root Of 325
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 12 And 5 Lcm . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.