12 Divided By 2
renascent
Sep 17, 2025 · 7 min read
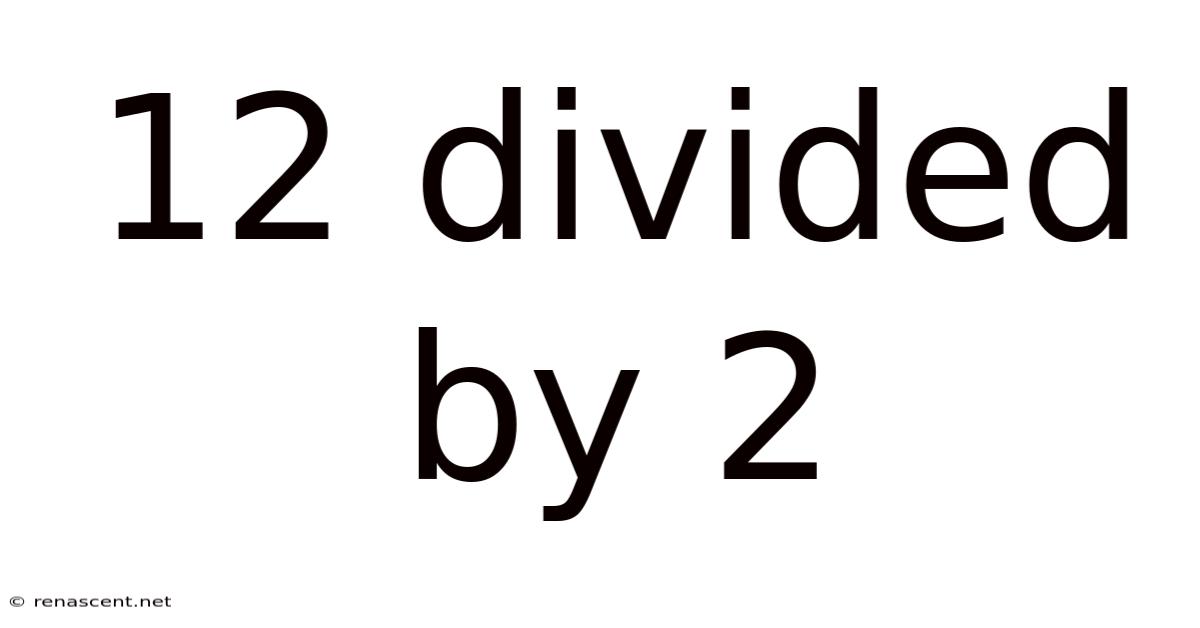
Table of Contents
12 Divided by 2: A Deep Dive into Simple Division
The seemingly simple equation, 12 divided by 2, or 12 ÷ 2, offers a gateway to understanding fundamental mathematical concepts. While the answer – 6 – is readily apparent to most, exploring this equation allows us to unpack the core principles of division, its various representations, and its applications across numerous fields. This exploration will go beyond a simple answer, delving into the underlying logic and demonstrating the multifaceted nature of this basic arithmetic operation.
Understanding Division: More Than Just Sharing
Division, at its heart, is the inverse operation of multiplication. While multiplication involves combining equal groups, division involves separating a quantity into equal groups or determining how many times one number is contained within another. In the case of 12 ÷ 2, we're asking: "How many times does 2 fit into 12?" or "If we divide 12 into 2 equal groups, how many items are in each group?"
The number being divided (12) is called the dividend. The number we're dividing by (2) is the divisor. The result (6) is the quotient. Understanding these terms is crucial for grasping the broader concepts of division.
Different Ways to Represent 12 ÷ 2
Mathematical notation can be surprisingly versatile. The equation "12 divided by 2" can be expressed in several ways:
- 12 ÷ 2: This is the most common notation, using the division symbol (÷).
- 12 / 2: This uses a forward slash (/), often preferred in computer programming and calculators.
- 12²⁄₂: This represents division as a fraction, where 12 is the numerator and 2 is the denominator. Fractions provide a powerful visual representation of division, showcasing the relationship between the dividend and the divisor.
All three notations represent the same mathematical operation and yield the same result: 6. Understanding these different notations is essential for navigating various mathematical contexts.
The Practical Applications of 12 ÷ 2
While seemingly simple, the concept of dividing 12 by 2 has widespread applications across various domains:
-
Everyday Life: Imagine sharing 12 cookies equally between 2 friends. The division 12 ÷ 2 helps determine that each friend receives 6 cookies. This simple application extends to countless scenarios involving sharing, distributing, or portioning resources.
-
Baking and Cooking: Recipes often require precise measurements. If a recipe calls for 12 ounces of flour and you want to halve the recipe, dividing 12 by 2 tells you that you need 6 ounces of flour.
-
Geometry and Measurement: Consider a rectangle with an area of 12 square units and a width of 2 units. Dividing 12 by 2 gives you the length of the rectangle (6 units). This principle extends to calculating various geometric properties.
-
Engineering and Physics: Many engineering and physics problems involve dividing quantities to determine rates, ratios, or other essential parameters. For example, calculating average speed might involve dividing total distance by total time.
-
Finance and Accounting: Dividing total expenses by the number of months calculates the average monthly expense. Dividing total profit by the number of units sold determines the profit per unit.
These examples highlight the ubiquitous nature of division in our daily lives and across various professional fields. Understanding this fundamental operation is essential for navigating these situations effectively.
Visualizing 12 ÷ 2: A Concrete Approach
For a deeper understanding, let's visualize 12 ÷ 2 using different methods:
-
Using Objects: Imagine 12 marbles. Separate them into two equal piles. Each pile will contain 6 marbles, visually demonstrating the result of 12 ÷ 2.
-
Using Number Lines: Start at 12 on a number line and jump back in increments of 2. The number of jumps required to reach 0 represents the quotient. In this case, you'll make 6 jumps, again illustrating that 12 ÷ 2 = 6.
-
Using Arrays: An array is a rectangular arrangement of objects. Create a rectangular array with 12 objects arranged in 2 rows. Counting the number of objects in each row shows that there are 6 objects per row, confirming the answer.
These visual methods help solidify the understanding of division, making the abstract concept more concrete and accessible, particularly for younger learners.
Connecting Division to Other Mathematical Operations
Division is intrinsically linked to other fundamental mathematical operations:
-
Multiplication: Division is the inverse of multiplication. The equation 12 ÷ 2 = 6 can be verified by multiplying the quotient (6) by the divisor (2) to get the dividend (12). This reciprocal relationship is key to understanding the underlying logic of division.
-
Subtraction: Division can also be viewed as repeated subtraction. Subtracting 2 from 12 repeatedly until you reach 0 will require 6 subtractions, demonstrating that 12 ÷ 2 = 6. This approach is particularly useful for illustrating the concept of division to beginners.
-
Fractions: As mentioned earlier, division can be represented as a fraction. The fraction 12/2 is equivalent to 12 ÷ 2, emphasizing the close relationship between these mathematical concepts.
Understanding these connections strengthens mathematical proficiency and promotes a more holistic understanding of numerical operations.
Exploring Division with Larger Numbers: Building on the Foundation
While 12 ÷ 2 is a simple example, understanding this operation lays the groundwork for solving more complex division problems. The same principles apply when dealing with larger numbers. For example:
-
120 ÷ 2: We can apply the same logic as 12 ÷ 2, recognizing that 120 is 10 times larger than 12. Therefore, the quotient will also be 10 times larger, resulting in 60.
-
1200 ÷ 20: This problem involves both larger dividends and divisors. We can break it down: 1200 is 100 times 12, and 20 is 10 times 2. Dividing 100 by 10 gives us 10, and multiplying this by the quotient of 12 ÷ 2 (which is 6) yields 60.
By applying the fundamental principles learned from 12 ÷ 2, we can confidently tackle more complex division problems. This emphasizes the importance of mastering basic operations as a foundation for advanced mathematical concepts.
Addressing Potential Challenges and Misconceptions
While division is a fundamental concept, some common misconceptions can arise:
-
Order of Operations: When dealing with multiple operations, the order of operations (PEMDAS/BODMAS) must be followed correctly. Division should be performed before addition or subtraction unless parentheses indicate otherwise.
-
Remainders: Not all division problems result in whole numbers. When the dividend is not perfectly divisible by the divisor, a remainder is obtained. For example, 13 ÷ 2 = 6 with a remainder of 1. Understanding remainders is crucial for handling real-world problems where perfect division isn't always possible.
-
Zero as a Divisor: Division by zero is undefined in mathematics. There is no numerical value that can satisfy the equation x * 0 = 12, making division by zero an impossible operation.
Addressing these potential challenges ensures a clear and accurate understanding of division and its applications.
Frequently Asked Questions (FAQs)
Q: What is the simplest way to explain 12 divided by 2 to a child?
A: Imagine you have 12 candies, and you want to share them equally between 2 friends. How many candies does each friend get? The answer is 6, because 12 ÷ 2 = 6.
Q: Why is division the inverse of multiplication?
A: Because multiplication combines equal groups, and division separates a quantity into equal groups. They are opposite operations that "undo" each other. If you multiply 6 by 2 you get 12; if you divide 12 by 2 you get 6.
Q: What if I have to divide 12 by a number other than 2?
A: The principle remains the same. You are still asking how many times that number fits into 12, or how many items would be in each group if you divided 12 into that many equal groups.
Conclusion: The Enduring Significance of a Simple Equation
The equation 12 ÷ 2 = 6, while seemingly simplistic, provides a powerful foundation for understanding fundamental mathematical principles. Its applications extend far beyond basic arithmetic, impacting numerous fields and everyday scenarios. By exploring this seemingly simple equation in depth, we’ve not only arrived at the answer but also gained a deeper appreciation for the interconnectedness of mathematical concepts and their practical relevance in our lives. Mastering this foundational operation paves the way for tackling more complex mathematical challenges and fosters a stronger sense of numerical reasoning.
Latest Posts
Latest Posts
-
9 X 3 2
Sep 17, 2025
-
6 Groups Of 5
Sep 17, 2025
-
Adr Approved Steering Wheels
Sep 17, 2025
-
What Does Ogn Mean
Sep 17, 2025
-
7 5 To A Fraction
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.