12 Divided By 8
renascent
Sep 24, 2025 · 6 min read
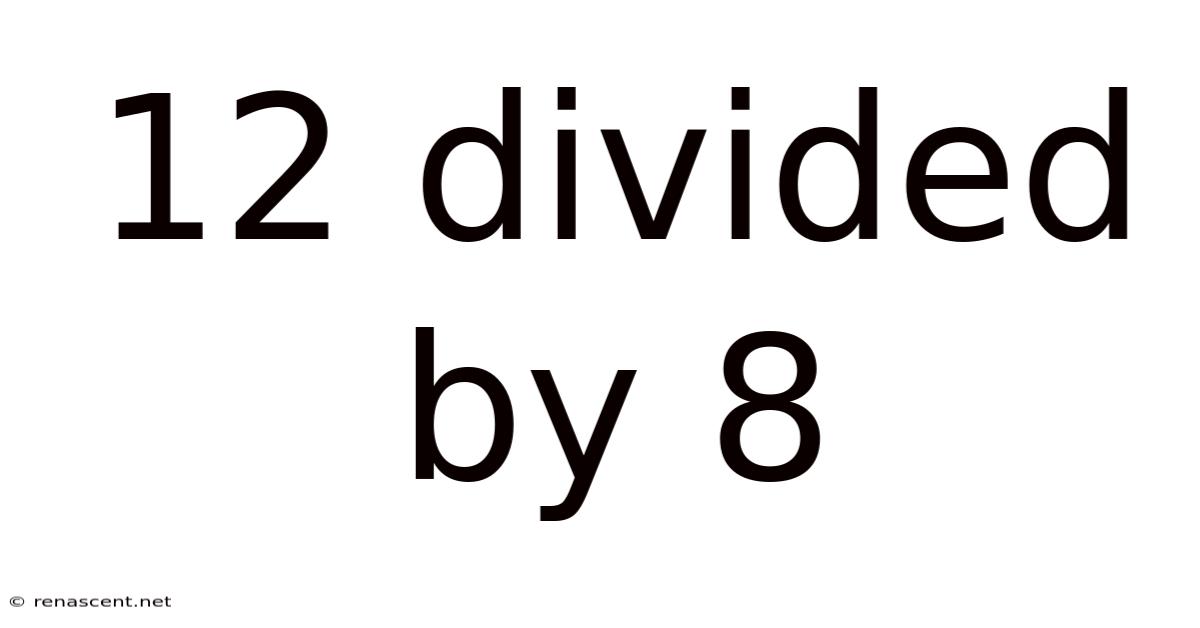
Table of Contents
Decoding 12 Divided by 8: A Deep Dive into Division and its Applications
Dividing 12 by 8 might seem like a simple arithmetic problem, something easily solved with a calculator. However, this seemingly straightforward calculation offers a gateway to understanding fundamental concepts in mathematics, including fractions, decimals, and the practical applications of division in everyday life. This article delves deep into the process of dividing 12 by 8, exploring various methods, interpretations, and real-world examples to provide a comprehensive understanding for learners of all levels.
Understanding Division: Beyond Simple Sharing
At its core, division is the process of splitting a quantity into equal parts. When we say "12 divided by 8," we're essentially asking: "If we have 12 items, and we want to divide them equally among 8 groups, how many items will be in each group?" This seemingly simple question opens up a world of mathematical exploration.
Method 1: Long Division – A Step-by-Step Approach
The traditional method for solving 12 divided by 8 involves long division. Here's how it works:
-
Set up the problem: Write 12 as the dividend (the number being divided) and 8 as the divisor (the number we're dividing by). This is typically represented as 8)12.
-
Determine the quotient: Ask yourself, "How many times does 8 go into 12?" The answer is 1. This is the whole number part of our answer, the quotient.
-
Multiply and subtract: Multiply the quotient (1) by the divisor (8), resulting in 8. Subtract this from the dividend (12): 12 - 8 = 4. This is the remainder.
-
Express the remainder: Because 8 doesn't go into 4, we have a remainder. This means our answer isn't a whole number. We can express this remainder as a fraction or a decimal.
-
Expressing as a fraction: The remainder (4) becomes the numerator of a fraction, and the divisor (8) becomes the denominator. Our answer is 1 and 4/8.
-
Simplifying the fraction: The fraction 4/8 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 4. This simplifies to 1/2.
Therefore, 12 divided by 8 is 1 and 1/2, or 1.5.
Method 2: Using Fractions – A Visual Approach
Another way to approach this problem is to express it directly as a fraction: 12/8. This fraction represents the division problem. We can then simplify this fraction by finding the greatest common divisor (GCD) of 12 and 8, which is 4. Dividing both the numerator and denominator by 4 gives us 3/2. This improper fraction can be converted into a mixed number: 1 and 1/2, or 1.5 as a decimal. This method provides a visual representation of the division process.
Method 3: Decimal Conversion – Precision and Accuracy
To express the answer as a decimal, we can perform long division as shown above, continuing the process beyond the remainder stage. After subtracting 8 from 12, we have a remainder of 4. We add a decimal point and a zero to the remainder, making it 40. Now, we ask how many times 8 goes into 40. The answer is 5. Thus, 12 divided by 8 is 1.5.
Understanding the Remainder – More than Just Leftovers
The remainder in division is crucial. It represents the portion of the dividend that couldn't be evenly distributed among the divisor groups. In the case of 12 divided by 8, the remainder of 4 signifies that after distributing 1 item to each of the 8 groups, we're left with 4 items. This remainder can be interpreted in several ways depending on the context. For instance, if we're dividing 12 pizzas among 8 people, the remainder represents the leftover pizza slices that need to be further divided or shared.
Real-World Applications of Division – From Baking to Budgeting
The concept of division permeates many aspects of our daily lives. Here are some examples:
-
Baking: A recipe calls for 12 ounces of flour, but you only have an 8-ounce measuring cup. You'll need to understand that you'll need to fill the cup once and a half.
-
Budgeting: You have $12 and you want to divide it equally among 8 charity donations. Division helps you determine how much you can donate to each charity.
-
Construction: Cutting a 12-foot piece of wood into 8 equal lengths requires calculating the length of each piece.
-
Sharing Resources: Equitably distributing resources like candy, toys, or workload among a group involves division.
Fractions and Decimals – Two Sides of the Same Coin
Understanding the relationship between fractions and decimals is vital. In the context of 12 divided by 8, we can see that the fraction 1 and 1/2 is equivalent to the decimal 1.5. Both representations accurately represent the result of the division. The choice between using fractions or decimals depends on the context and the required level of precision. Fractions are often preferred when dealing with discrete quantities (like items), while decimals are more convenient for continuous quantities (like measurements).
Beyond the Basics – Exploring More Complex Division
While 12 divided by 8 is a relatively simple problem, it serves as a foundation for understanding more complex division problems. This includes dividing larger numbers, working with negative numbers, and performing division with decimals and fractions. Mastering the basic principles is essential for tackling these more advanced scenarios.
Frequently Asked Questions (FAQ)
-
Q: What is the remainder when 12 is divided by 8?
-
A: The remainder is 4.
-
Q: Can I use a calculator to solve this problem?
-
A: Yes, a calculator will quickly provide the answer as 1.5. However, understanding the underlying process is more valuable than just obtaining the numerical result.
-
Q: What if I needed to divide 12 by 8.5?
-
A: Dividing by decimals requires a slightly different approach, typically involving multiplying both the dividend and divisor by a power of 10 to eliminate the decimal point before applying long division or using a calculator.
-
Q: What are some real-world applications of division beyond the examples mentioned?
-
A: There are countless other applications. Examples include calculating fuel efficiency (miles per gallon), determining unit prices (price per ounce), or even sharing expenses among friends.
Conclusion: Mastering the Fundamentals
While seemingly simple, the division problem 12 divided by 8 offers a rich opportunity to explore fundamental mathematical concepts. From understanding the different methods for solving division problems to appreciating the significance of the remainder and the equivalence of fractions and decimals, this problem highlights the practical application of mathematics in various everyday situations. By grasping these core principles, learners can build a solid mathematical foundation that extends to more complex challenges in the future. The key takeaway is not just the answer (1.5), but the process of arriving at the answer and understanding what it truly represents. This understanding empowers us to confidently tackle similar problems and apply the principles of division to numerous real-world scenarios.
Latest Posts
Latest Posts
-
17 Divided By 4
Sep 24, 2025
-
1055 Kj To Calories
Sep 24, 2025
-
A Ti Te Gustan
Sep 24, 2025
-
62 F In Celsius
Sep 24, 2025
-
1 2 Teaspoon Vanilla Extract
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.