124 Divided By 4
renascent
Sep 15, 2025 · 5 min read
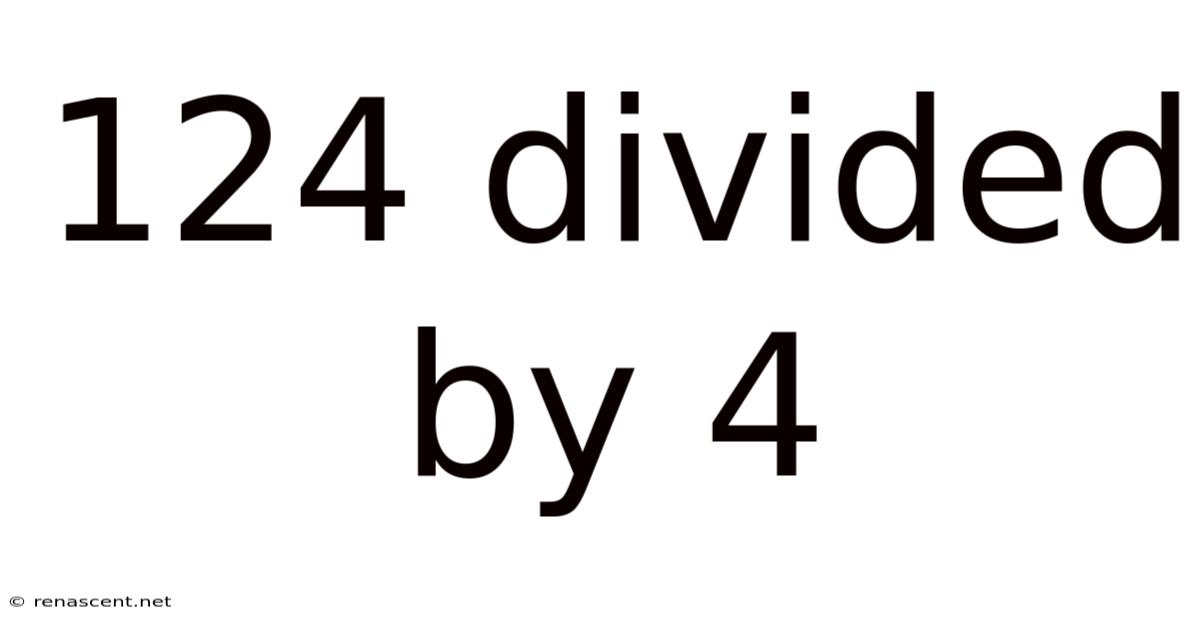
Table of Contents
Unpacking 124 Divided by 4: A Deep Dive into Division
This article explores the seemingly simple division problem, 124 divided by 4, delving far beyond the immediate answer. We'll examine the process using various methods, understand the underlying mathematical concepts, explore real-world applications, and even touch upon the historical context of division. By the end, you'll not only know the answer but also gain a much deeper appreciation for this fundamental arithmetic operation.
Understanding the Problem: 124 ÷ 4
The expression "124 divided by 4" asks: how many times does 4 fit into 124? This seemingly simple question forms the basis of many complex mathematical concepts. It's a foundational element in algebra, calculus, and countless applications in science, engineering, and everyday life. We'll break down the solution using several methods, each illuminating different aspects of division.
Method 1: Long Division
Long division is a classical method for solving division problems, particularly useful for larger numbers. Here's how we approach 124 ÷ 4 using long division:
-
Set up the problem: Write 124 inside the long division symbol (⟌) and 4 outside.
4 ⟌ 124 -
Divide the hundreds: How many times does 4 go into 1? It doesn't, so we move to the tens place. How many times does 4 go into 12? It goes 3 times (3 x 4 = 12). Write the 3 above the 2 in 124.
3 4 ⟌ 124 -
Multiply and subtract: Multiply 3 by 4 (3 x 4 = 12) and write the result below the 12. Subtract 12 from 12, resulting in 0.
3 4 ⟌ 124 -12 0 -
Bring down the next digit: Bring down the 4 from 124.
3 4 ⟌ 124 -12 04 -
Divide the remaining digits: How many times does 4 go into 4? It goes 1 time (1 x 4 = 4). Write the 1 above the 4 in 124.
31 4 ⟌ 124 -12 04 -
Multiply and subtract: Multiply 1 by 4 (1 x 4 = 4) and write the result below the 4. Subtract 4 from 4, resulting in 0.
31 4 ⟌ 124 -12 04 -4 0
Therefore, 124 divided by 4 is 31.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the divisor (4) from the dividend (124) until the result is 0 or less than the divisor. The number of times you subtract is the quotient.
- Start with 124: 124 - 4 = 120
- Subtract 4 repeatedly:
- 120 - 4 = 116
- 116 - 4 = 112
- 112 - 4 = 108
- 108 - 4 = 104
- 104 - 4 = 100
- 100 - 4 = 96
- 96 - 4 = 92
- 92 - 4 = 88
- 88 - 4 = 84
- 84 - 4 = 80
- 80 - 4 = 76
- 76 - 4 = 72
- 72 - 4 = 68
- 68 - 4 = 64
- 64 - 4 = 60
- 60 - 4 = 56
- 56 - 4 = 52
- 52 - 4 = 48
- 48 - 4 = 44
- 44 - 4 = 40
- 40 - 4 = 36
- 36 - 4 = 32
- 32 - 4 = 28
- 28 - 4 = 24
- 24 - 4 = 20
- 20 - 4 = 16
- 16 - 4 = 12
- 12 - 4 = 8
- 8 - 4 = 4
- 4 - 4 = 0
We subtracted 4 a total of 31 times. Therefore, 124 divided by 4 is 31. While effective for smaller numbers, this method becomes cumbersome for larger ones.
Method 3: Factoring
This method uses prime factorization to simplify the division. We first find the prime factors of both 124 and 4.
- Prime factorization of 124: 2 x 2 x 31 = 2² x 31
- Prime factorization of 4: 2 x 2 = 2²
Now, we can rewrite the division as: (2² x 31) / 2²
Since 2² is in both the numerator and denominator, they cancel out, leaving us with 31.
Therefore, 124 divided by 4 is 31. This method showcases the underlying mathematical structure of the division process.
Real-World Applications
Division, as represented by 124 ÷ 4, is ubiquitous in daily life:
- Sharing: If you have 124 candies and want to share them equally among 4 friends, each friend receives 31 candies.
- Measurement: If a road is 124 meters long and you need to divide it into 4 equal sections, each section is 31 meters long.
- Averaging: If you scored 124 points over 4 games, your average score per game is 31 points.
- Unit conversion: Many unit conversions involve division. For example, converting inches to feet might involve dividing the total inches by 12 (inches per foot). While not directly related to our example, the principle is the same.
The Mathematical Foundation: Divisibility Rules
Understanding divisibility rules can help you quickly determine if a number is divisible by another without performing the actual division. While there isn't a specific rule for divisibility by 31, we can use the divisibility rule for 4.
- Divisibility Rule for 4: A number is divisible by 4 if its last two digits are divisible by 4. In 124, the last two digits are 24, which is divisible by 4 (24 ÷ 4 = 6). This rule quickly confirms that 124 is divisible by 4, although it doesn't give the quotient directly.
Frequently Asked Questions (FAQ)
-
Q: What if the division didn't result in a whole number? A: If the dividend (124) wasn't perfectly divisible by the divisor (4), the result would have a remainder. For example, 125 ÷ 4 would be 31 with a remainder of 1.
-
Q: Are there other ways to solve this problem? A: Yes, calculators and computer programs provide quick solutions. However, understanding the underlying methods (long division, repeated subtraction, factoring) provides a deeper understanding of the mathematical principles.
-
Q: Why is division important? A: Division is a fundamental arithmetic operation essential for problem-solving in various fields, from basic accounting to advanced engineering and scientific research.
Conclusion: More Than Just an Answer
While the answer to 124 divided by 4 is simply 31, this article aimed to go beyond the immediate solution. By exploring different methods and examining the underlying mathematical concepts, we’ve shown that even a seemingly basic arithmetic problem holds significant depth and practical relevance. Understanding the "why" behind the "how" is crucial for developing a strong mathematical foundation and applying these skills effectively in real-world situations. The journey of understanding 124 divided by 4 has hopefully illuminated the beauty and power of division as a fundamental mathematical tool.
Latest Posts
Related Post
Thank you for visiting our website which covers about 124 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.