13/20 As A Percentage
renascent
Sep 17, 2025 · 5 min read
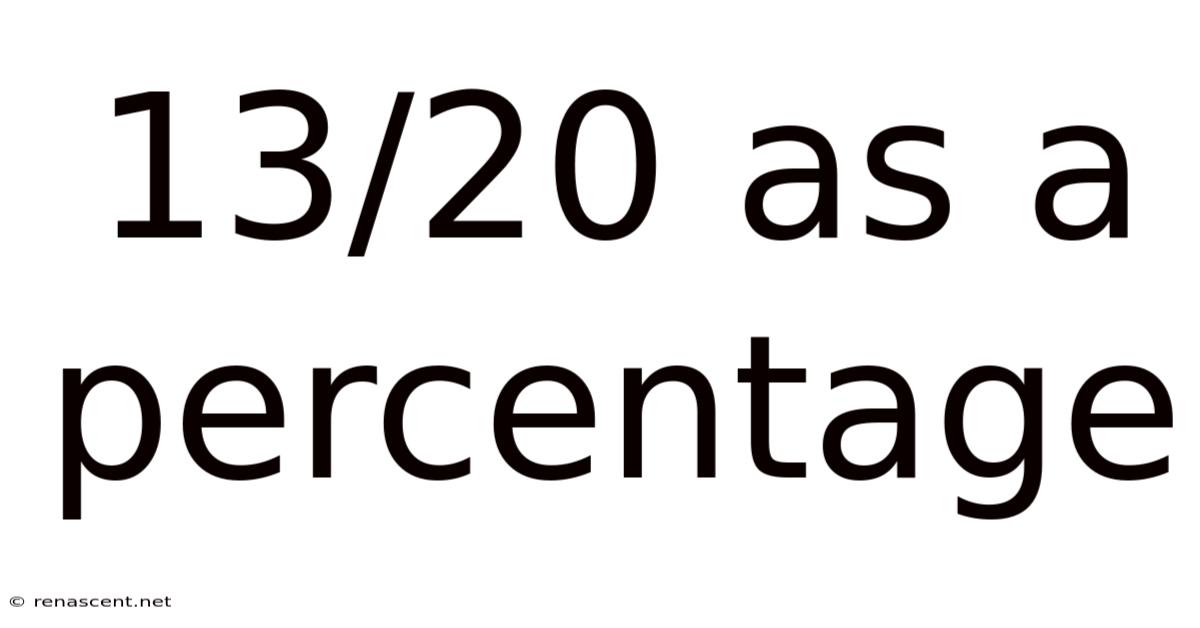
Table of Contents
13/20 as a Percentage: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications across numerous fields, from calculating grades to analyzing financial data. This comprehensive guide will delve into the process of converting 13/20 into a percentage, providing a step-by-step explanation, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also explore various methods and practical applications to solidify your understanding. This guide aims to be a valuable resource for students, educators, and anyone seeking a deeper grasp of percentage calculations.
Understanding Fractions and Percentages
Before we dive into the conversion of 13/20, let's establish a clear understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts that make up the whole. For example, in the fraction 13/20, 13 is the numerator and 20 is the denominator. This means we have 13 parts out of a possible 20 parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion or ratio as a number out of one hundred. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. Percentages are widely used to express proportions in various contexts, making them easily comparable and understandable.
Converting 13/20 to a Percentage: The Step-by-Step Method
There are several ways to convert a fraction to a percentage. The most straightforward method involves two key steps:
Step 1: Convert the fraction to a decimal.
To convert 13/20 to a decimal, we simply divide the numerator (13) by the denominator (20):
13 ÷ 20 = 0.65
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.65 × 100 = 65%
Therefore, 13/20 is equal to 65%.
Alternative Methods for Conversion
While the above method is the most common and straightforward, there are alternative approaches you can use:
Method 1: Finding an Equivalent Fraction with a Denominator of 100
We can convert 13/20 to an equivalent fraction with a denominator of 100. Since percentages are based on 100, this method directly provides the percentage. To do this, we need to find a number that, when multiplied by 20, equals 100. That number is 5 (20 x 5 = 100). We then multiply both the numerator and the denominator by 5:
(13 x 5) / (20 x 5) = 65/100
Since 65/100 means 65 out of 100, this directly translates to 65%.
Method 2: Using Proportions
We can set up a proportion to solve for the percentage:
13/20 = x/100
To solve for x (the percentage), we cross-multiply:
20x = 1300
x = 1300 ÷ 20
x = 65
Therefore, 13/20 is equivalent to 65%.
The Mathematical Principles Behind the Conversion
The conversion from fractions to percentages relies on the fundamental concept of proportionality. A percentage is simply a fraction expressed as a part of 100. The process of converting a fraction to a percentage essentially involves scaling the fraction to a denominator of 100, which reveals the equivalent percentage. Multiplying by 100% (which is equivalent to 1) does not change the value of the fraction, only its representation.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world situations. Here are a few examples:
- Academic Performance: Calculating grades based on scores obtained out of a total. If a student scores 13 out of 20 on a test, their percentage score is 65%.
- Financial Calculations: Determining interest rates, discounts, profit margins, and tax percentages.
- Data Analysis: Representing proportions and trends in data sets using percentages. For example, if a survey shows that 13 out of 20 respondents prefer a particular product, it can be stated that 65% of the respondents prefer that product.
- Everyday Life: Calculating tips, sales tax, and discounts in shopping situations.
Frequently Asked Questions (FAQ)
Q1: What if the fraction doesn't easily convert to a denominator of 100?
A1: If the denominator doesn't easily convert to 100, the best approach is to convert the fraction to a decimal first by dividing the numerator by the denominator and then multiplying the resulting decimal by 100 to obtain the percentage.
Q2: Can I use a calculator to convert fractions to percentages?
A2: Absolutely! Most calculators have a function that allows you to directly input a fraction and obtain its decimal and percentage equivalent.
Q3: What does it mean if a percentage is greater than 100%?
A3: A percentage greater than 100% indicates that the part is larger than the whole. This often occurs when comparing changes or growth over time. For example, if sales increase from 20 units to 26 units, the percentage increase is 30%, or 130% of the original amount.
Q4: How can I improve my understanding of percentage calculations?
A4: Practice is key! Work through various examples of fraction-to-percentage conversions, using different methods. You can find plenty of practice exercises online or in math textbooks. Understanding the underlying principles of proportionality is also essential.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. This guide has explored the conversion of 13/20 to 65%, using multiple methods and explaining the underlying mathematical principles. By understanding these methods and practicing their application, you can confidently tackle similar percentage conversions in various academic and real-world situations. Remember that mastering this skill builds a strong foundation for more complex mathematical concepts and problem-solving. The key takeaway is that 13/20 represents 65% – a simple yet powerful concept that underpins numerous practical calculations.
Latest Posts
Latest Posts
-
123 Pounds In Kilos
Sep 18, 2025
-
Square Root Of 130
Sep 18, 2025
-
Activity On Node Diagram
Sep 18, 2025
-
26 2 Miles In K
Sep 18, 2025
-
Clock Showing 2 30
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 13/20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.