13 Divided By 4
renascent
Sep 21, 2025 · 5 min read
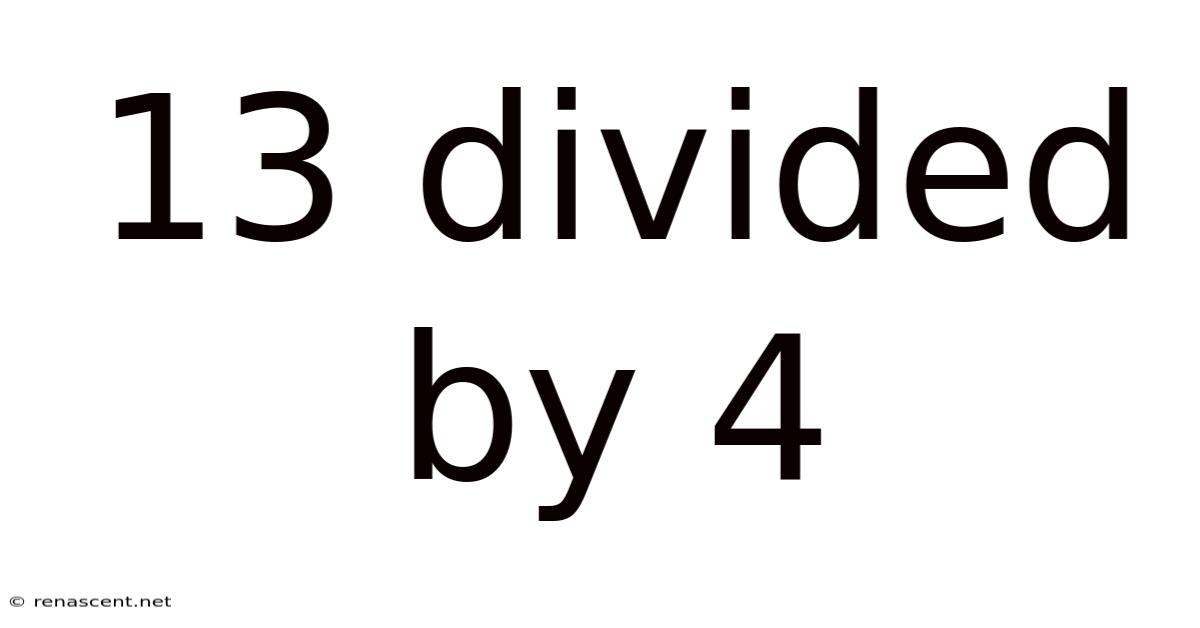
Table of Contents
13 Divided by 4: Unveiling the Magic of Division and Remainders
Dividing 13 by 4 might seem like a simple arithmetic problem, but it opens a door to understanding fundamental concepts in mathematics, particularly division, remainders, fractions, and decimals. This comprehensive guide will delve into the intricacies of this seemingly basic calculation, exploring various approaches and illuminating the underlying principles. We'll move beyond simply stating the answer and explore the deeper meaning and applications of this seemingly simple division problem.
Introduction: Beyond the Simple Answer
At its most basic level, 13 divided by 4 (written as 13 ÷ 4 or 13/4) asks: how many times does 4 fit completely into 13? The straightforward answer is 3, but that leaves something leftover. This "leftover" is crucial; it's the remainder. Understanding how to handle the remainder is key to mastering division and its applications in various mathematical contexts. This article will guide you through different methods of calculating this division problem, explaining the significance of both the quotient (the result of the division) and the remainder.
Method 1: Long Division – A Classic Approach
Long division is a traditional method for solving division problems, especially those involving larger numbers. Let's apply it to 13 ÷ 4:
-
Set up the problem: Write 13 inside the long division symbol (⟌) and 4 outside.
4 ⟌ 13 -
Divide: How many times does 4 go into 1? It doesn't, so we move to the next digit. How many times does 4 go into 13? It goes in 3 times (3 x 4 = 12). Write the 3 above the 3 in 13.
3 4 ⟌ 13 -
Multiply: Multiply the quotient (3) by the divisor (4): 3 x 4 = 12. Write 12 below the 13.
3 4 ⟌ 13 12 -
Subtract: Subtract 12 from 13: 13 - 12 = 1. This is the remainder.
3 4 ⟌ 13 12 -- 1
Therefore, 13 divided by 4 is 3 with a remainder of 1. This can be expressed as 3 R1.
Method 2: Repeated Subtraction – A Conceptual Approach
Repeated subtraction provides a more intuitive understanding of division. We repeatedly subtract the divisor (4) from the dividend (13) until we reach a number smaller than the divisor.
- Start with 13: 13 - 4 = 9
- Subtract again: 9 - 4 = 5
- Subtract again: 5 - 4 = 1
We subtracted 4 three times before reaching a number (1) less than 4. This confirms that 4 goes into 13 three times with a remainder of 1.
Method 3: Fraction Representation – Unveiling the Decimal Equivalent
Instead of focusing solely on the whole number quotient and remainder, we can express the division as a fraction: 13/4. This fraction represents 13 parts out of a total of 4 parts. To find the decimal equivalent, we perform the long division as shown before, but we continue beyond the remainder:
3.25
4 ⟌ 13.00
12
--
10
8
--
20
20
--
0
By adding a decimal point and zeros to the dividend, we can continue the division until we reach a zero remainder or a repeating decimal. This shows that 13/4 is equal to 3.25. This decimal representation is crucial for many practical applications.
Method 4: Using the Euclidean Algorithm
The Euclidean algorithm is a more formal method for finding the greatest common divisor (GCD) of two numbers, but it also implicitly solves the division problem. While less intuitive for this specific problem, it's valuable for understanding more complex division scenarios:
The Euclidean algorithm involves repeatedly applying the division algorithm until the remainder is zero. In this case:
13 = 4 * 3 + 1
The quotient is 3, and the remainder is 1.
Understanding the Remainder: Its Significance
The remainder (1 in this case) isn't just a leftover; it represents the portion of the dividend that wasn't fully divisible by the divisor. Its significance expands into various contexts:
- Real-world applications: If you have 13 cookies and want to divide them equally among 4 friends, each friend gets 3 cookies, and you have 1 cookie left over.
- Modular arithmetic: In modular arithmetic, the remainder is the key focus. For example, 13 modulo 4 (written as 13 mod 4) is 1. This has applications in cryptography and computer science.
- Further calculations: The remainder can be used in subsequent calculations or considered separately depending on the context of the problem.
Practical Applications of 13 Divided by 4
The seemingly simple problem of 13 divided by 4 has practical applications across diverse fields:
- Resource allocation: Dividing resources (e.g., budget, materials) among groups or individuals.
- Measurement and conversion: Converting units of measurement (e.g., inches to feet).
- Data analysis: Calculating averages or proportions.
- Programming and algorithms: Developing algorithms that involve division and remainder calculations.
- Number theory: Exploring concepts of divisibility, primes, and modular arithmetic.
Extending the Concept: Division with Larger Numbers
The principles illustrated with 13 divided by 4 apply to division problems involving much larger numbers. The long division method remains a cornerstone, while understanding the meaning of the remainder and its implications remains crucial.
Frequently Asked Questions (FAQs)
-
Q: What is the quotient when 13 is divided by 4?
- A: The quotient is 3.
-
Q: What is the remainder when 13 is divided by 4?
- A: The remainder is 1.
-
Q: How can I express 13/4 as a decimal?
- A: 13/4 = 3.25
-
Q: What are some real-world applications of division with remainders?
- A: Dividing tasks among a team, sharing items equally, converting units, and many more.
-
Q: Is there a way to check my answer after dividing?
- A: Yes, you can check your answer using the formula: (Quotient x Divisor) + Remainder = Dividend. In this case, (3 x 4) + 1 = 13.
Conclusion: A Deeper Dive into Division
The seemingly straightforward division of 13 by 4 opens a window into a world of mathematical concepts. This article not only provides the answer (3 with a remainder of 1, or 3.25) but also delves into the underlying principles, exploring various methods and highlighting the importance of the remainder. By understanding the various approaches and the significance of the quotient and remainder, you gain a stronger foundation in mathematics and enhance your ability to solve more complex problems. The seemingly simple act of dividing 13 by 4 illuminates the power and versatility of division in various real-world applications. Remember, understanding the "why" behind the calculations is just as important as knowing the "how."
Latest Posts
Latest Posts
-
Quotes About John Proctor
Sep 21, 2025
-
4 Of 100 000
Sep 21, 2025
-
4 X 5 3
Sep 21, 2025
-
19 24 X 100
Sep 21, 2025
-
Open Source Software Drawbacks
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 13 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.