4 X 5 3
renascent
Sep 21, 2025 · 6 min read
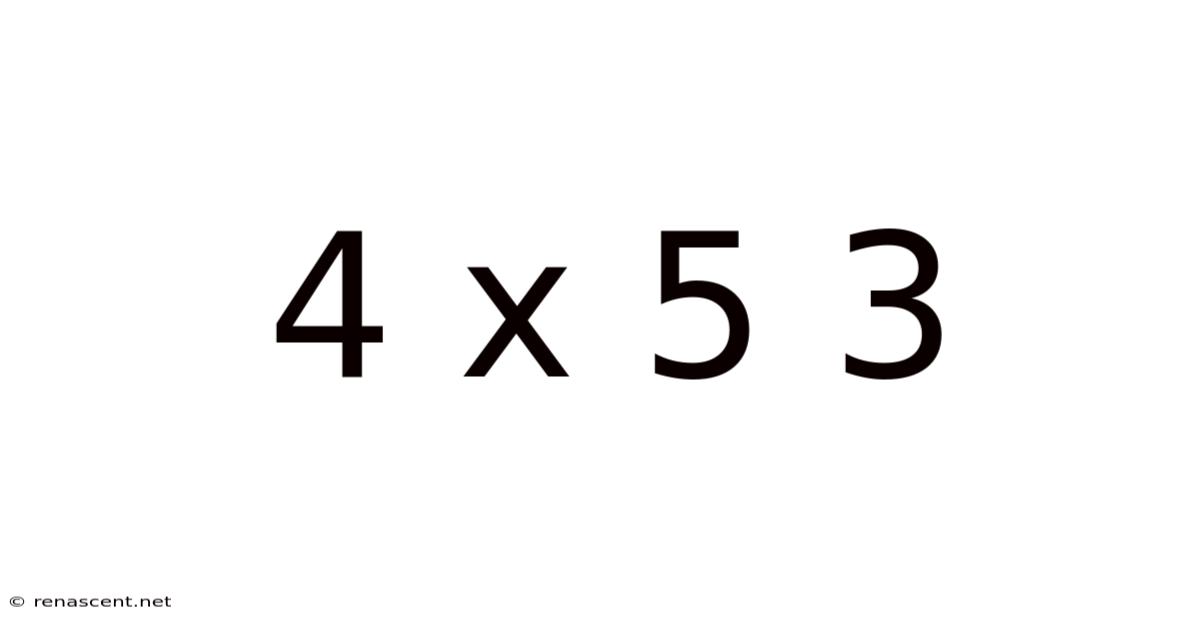
Table of Contents
Decoding the Enigma: Understanding 4 x 5 = 3 (and Why It's Not True)
The statement "4 x 5 = 3" is, unequivocally, false within the standard framework of arithmetic. However, understanding why it's false, and exploring the contexts where similar-looking equations might hold true, opens a fascinating door to various mathematical concepts. This article delves into the fundamental principles of multiplication, explores potential misinterpretations, and examines related mathematical ideas to illuminate the truth behind this seemingly simple equation.
Introduction: The Basics of Multiplication
Before tackling the apparent contradiction of 4 x 5 = 3, let's solidify our understanding of multiplication. Multiplication is essentially repeated addition. When we say 4 x 5, we are essentially saying "add 4 to itself 5 times," or 4 + 4 + 4 + 4 + 4, which equals 20. This fundamental principle is the cornerstone of arithmetic and forms the basis for all higher-level mathematical operations. The numbers involved (4 and 5 in this case) are called factors, and the result (20) is the product. The "x" symbol represents the multiplication operation.
Why 4 x 5 ≠ 3: A Clear Refutation
The equation 4 x 5 = 3 is incorrect because it violates the fundamental principle of multiplication. As we've established, 4 x 5 is equivalent to adding four five times, resulting in 20, not 3. There's no mathematical operation or legitimate interpretation within standard arithmetic that can justify this equation. This is a crucial point to understand: mathematical truths are based on consistently applied rules and axioms. Deviating from these rules leads to incorrect conclusions.
Potential Sources of Confusion: Misunderstandings and Misinterpretations
While the equation is clearly false in standard arithmetic, exploring potential sources of confusion can be instructive. Some possible scenarios that might lead to this misconception include:
- Typographical errors: A simple typing mistake could have resulted in the incorrect equation. Human error is a common factor in data entry and calculations.
- Misunderstanding of mathematical symbols: Confusion over the multiplication symbol "x" or the equals sign "=" could lead to a misinterpretation of the equation.
- Contextual errors: The equation might be taken out of context, perhaps from a puzzle or a riddle where unconventional rules are applied.
Exploring Related Mathematical Concepts: Modular Arithmetic and Group Theory
While 4 x 5 = 3 is false in standard arithmetic, similar-looking equations can be true within different mathematical frameworks. Let's explore a couple of these:
-
Modular Arithmetic (Clock Arithmetic): Modular arithmetic operates within a defined range of numbers. For instance, consider a 12-hour clock. If it's 8 o'clock and you add 5 hours, you don't get 13 o'clock; you get 1 o'clock. This is because we are operating modulo 12 (meaning we consider only the remainder after division by 12). In modular arithmetic, we can express this as 8 + 5 ≡ 1 (mod 12). Similarly, we could potentially construct a system where multiplication operates in a modular fashion, but finding a system where 4 x 5 ≡ 3 (mod n) for some integer 'n' would require a specific modulo and is not a straightforward or common occurrence.
-
Group Theory: Group theory deals with abstract algebraic structures. It's possible to define groups where the multiplication operation isn't standard multiplication but follows different rules. However, such groups would require defining a specific operation and set of elements, which is far beyond the scope of a simple equation like 4 x 5 = 3. Constructing a group where this equation holds would require a highly specific and non-intuitive definition of the group operation.
Mathematical Operations Beyond Standard Arithmetic: Exploring Alternative Systems
While standard arithmetic provides a consistent and reliable framework for numerical calculations, other mathematical systems exist with different rules and operations. These systems can produce results that might seem counter-intuitive from the perspective of traditional arithmetic.
- Boolean Algebra: This system uses only two values, 0 and 1, representing true and false. Operations like AND, OR, and NOT are used instead of addition and multiplication. It has no direct relationship to the equation 4 x 5 = 3.
- Abstract Algebra: This broad field encompasses various algebraic structures, such as rings, fields, and vector spaces, which use operations that can be vastly different from standard arithmetic. While they are far more complex, these systems can define operations that would not correspond to standard multiplication.
The Importance of Defining the System: Context is Key
The key takeaway from exploring these alternative systems is the importance of defining the system within which an equation is evaluated. Without specifying the rules of the system (whether it's standard arithmetic, modular arithmetic, or a more abstract system), the equation 4 x 5 = 3 remains inherently meaningless. Context is crucial for interpreting mathematical statements correctly.
Addressing Common Questions (FAQ)
Q: Are there any mathematical tricks or puzzles where 4 x 5 = 3 might be considered a valid solution?
A: It's highly unlikely. While there are many mathematical puzzles and riddles that use unconventional rules or interpretations, it's improbable that one would legitimately define a system where 4 x 5 equals 3. Any such "solution" would most likely involve a misdirection or trick, rather than a genuine mathematical operation.
Q: Could this equation be valid in a different base number system?
A: No. Changing the base number system (e.g., from base 10 to base 2 or base 16) alters the representation of numbers, but it does not change the fundamental principles of multiplication. The product of 4 and 5 remains 20 regardless of the base system used. The representation of 20 might change (e.g., 20 in base 10 is 10100 in base 2), but the numerical value remains the same.
Q: Is there a hidden pattern or secret code behind this equation?
A: There's no hidden mathematical pattern or secret code behind this equation. It's simply an incorrect equation within the standard framework of arithmetic. Attributing hidden meanings to incorrect mathematical statements is generally unproductive and misleading.
Q: How can I avoid making similar mistakes in my own calculations?
A: Double-check your work! Carefully review your calculations and ensure that you're applying the correct mathematical operations and rules. Pay attention to detail and use appropriate tools (calculators or software) when needed. A strong foundation in basic arithmetic is crucial for preventing such errors.
Conclusion: The Enduring Truth of Mathematical Principles
The equation "4 x 5 = 3" is demonstrably false within the established framework of arithmetic. While exploring alternative mathematical systems can reveal fascinating concepts and broaden our understanding of mathematics, it is crucial to always be aware of the context and the rules of the system being used. The strength and reliability of mathematics come from the consistent application of its fundamental principles. Understanding these principles is essential not only for solving mathematical problems but also for critical thinking in various aspects of life. The inherent beauty and power of mathematics lies in its consistency and its ability to describe the world around us with precision and accuracy. The equation 4 x 5 = 3 serves as a potent reminder of the importance of accurate calculations and the value of a solid foundation in basic mathematical concepts.
Latest Posts
Latest Posts
-
10 15 As A Percent
Sep 22, 2025
-
10 Of 300 00
Sep 22, 2025
-
230 C To Fahrenheit
Sep 22, 2025
-
Diagram Of A Beehive
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 4 X 5 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.