13 Divided By 5
renascent
Sep 19, 2025 · 6 min read
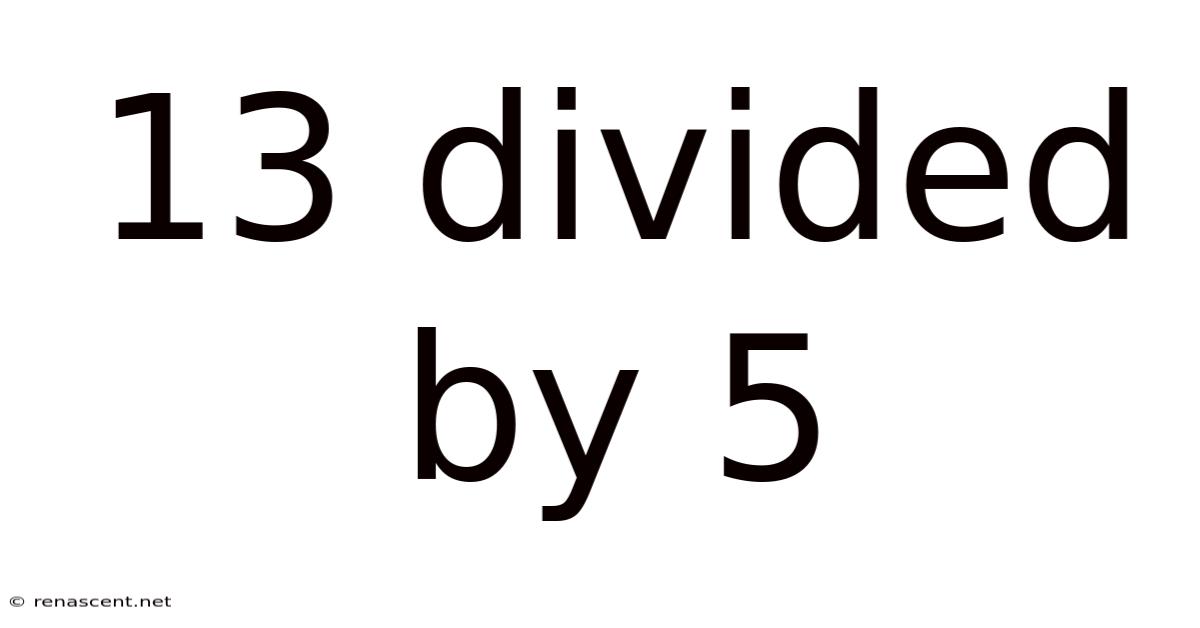
Table of Contents
Exploring the Division: 13 Divided by 5 – A Deep Dive into Fractions, Decimals, and Remainders
Dividing 13 by 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation offers a rich opportunity to explore fundamental mathematical concepts, including fractions, decimals, and the crucial idea of remainders. Understanding these concepts lays the groundwork for more advanced mathematical studies. This article will delve into the various ways to solve 13 divided by 5, explaining the underlying principles and demonstrating their practical applications.
Introduction: The Problem and its Context
The core problem is simple: 13 ÷ 5 = ? This expression asks, "How many times does 5 go into 13?" While the answer might seem immediately apparent to some, the nuances of this division problem are surprisingly profound. We will investigate different approaches to finding the solution, highlighting the strengths and limitations of each method. This exploration will build a strong foundation for understanding more complex division problems and related mathematical concepts.
Method 1: Long Division – A Classic Approach
Long division is a traditional method for solving division problems, especially those involving larger numbers. Let's apply it to 13 divided by 5:
-
Set up the problem: Write the dividend (13) inside the long division symbol and the divisor (5) outside.
5 | 13 -
Divide: How many times does 5 go into 13? It goes in 2 times (5 x 2 = 10). Write the 2 above the 3 in the dividend.
2 5 | 13 -
Multiply: Multiply the quotient (2) by the divisor (5): 2 x 5 = 10. Write this below the 13.
2 5 | 13 10 -
Subtract: Subtract the product (10) from the dividend (13): 13 - 10 = 3. Write the difference below the 10.
2 5 | 13 10 --- 3 -
Interpret the Remainder: The result, 3, is the remainder. This means that 5 goes into 13 two times with 3 left over. We can express this as 2 with a remainder of 3, often written as 2 R 3.
Therefore, using long division, 13 ÷ 5 = 2 R 3.
Method 2: Fractions – Representing the Remainder
Instead of expressing the remainder as "R 3," we can incorporate it into a fraction. The remainder (3) becomes the numerator, and the divisor (5) becomes the denominator:
13 ÷ 5 = 2 and 3/5
This fraction, 3/5, represents the portion of 5 that is left over after dividing 13 by 5. This approach provides a more precise and mathematically elegant way of representing the result. The answer is 2 3/5, a mixed number combining a whole number (2) and a fraction (3/5).
Method 3: Decimals – Extending the Division
We can extend the long division process to obtain a decimal answer. To do this, we add a decimal point and zeros to the dividend:
-
Add a decimal point and zero:
2. 5 | 13.0 10 --- 3 -
Bring down the zero: Bring down the zero to make 30.
2. 5 | 13.0 10 --- 30 -
Continue dividing: How many times does 5 go into 30? It goes in 6 times (5 x 6 = 30). Write the 6 after the decimal point.
2.6 5 | 13.0 10 --- 30 30 --- 0
Therefore, using decimal representation, 13 ÷ 5 = 2.6.
Understanding the Relationship Between Fractions and Decimals
The fraction 3/5 and the decimal 0.6 are equivalent representations of the same value. To convert a fraction to a decimal, you divide the numerator by the denominator: 3 ÷ 5 = 0.6. Conversely, to convert a decimal to a fraction, you write the decimal as a fraction with a power of 10 as the denominator and simplify. For example, 0.6 can be written as 6/10, which simplifies to 3/5. This demonstrates the interconnectedness of these mathematical concepts.
Real-World Applications
Understanding division with remainders has many practical applications:
-
Sharing: If you have 13 cookies and want to share them equally among 5 friends, each friend gets 2 cookies, and you have 3 cookies left over.
-
Measurement: If you need to cut a 13-meter rope into 5 equal pieces, each piece will be 2.6 meters long.
-
Pricing: If 5 identical items cost $13, each item costs $2.60.
-
Resource Allocation: If you have 13 liters of paint and each wall requires 5 liters, you can paint 2 walls completely and have 3 liters left.
Further Exploration: Modular Arithmetic
The remainder in a division problem is a key concept in modular arithmetic, a branch of number theory. In the context of 13 ÷ 5, the remainder of 3 signifies that 13 is congruent to 3 modulo 5, written as 13 ≡ 3 (mod 5). This means that 13 and 3 leave the same remainder when divided by 5. Modular arithmetic has applications in cryptography, computer science, and other fields.
Frequently Asked Questions (FAQ)
Q1: Why are there different ways to represent the answer to 13 ÷ 5?
A1: The different representations (2 R 3, 2 3/5, and 2.6) highlight different aspects of the division. The remainder emphasizes the "leftovers," the fraction provides a precise representation of the whole, and the decimal offers a convenient form for calculations. The best representation depends on the context of the problem.
Q2: Is it always necessary to use a decimal representation?
A2: Not necessarily. In some situations, a fraction or a remainder is more appropriate or even necessary. For example, you cannot have 0.6 of a cookie, but you can have 3/5 of a cookie.
Q3: Can you explain the concept of a "remainder" more thoroughly?
A3: The remainder is the amount left over after a division operation when the dividend is not perfectly divisible by the divisor. It indicates that the division is not exact and represents the portion of the dividend that cannot be evenly distributed among the divisor.
Q4: What happens if the divisor is zero?
A4: Dividing by zero is undefined in mathematics. It's a fundamental rule that you cannot divide by zero.
Q5: How does this relate to more complex division problems?
A5: The principles of long division, fractions, decimals, and remainders all apply to more complex division problems. The process remains the same, even if the numbers are larger or involve more steps. The ability to understand and apply these concepts forms the foundation for handling much more challenging calculations.
Conclusion: Beyond the Simple Calculation
While the problem of 13 divided by 5 might appear trivial, it provides a valuable opportunity to reinforce crucial mathematical concepts. By exploring the different methods of solving this problem and understanding the relationship between fractions, decimals, and remainders, we gain a deeper appreciation for the elegance and practicality of mathematics. This understanding is not just about solving simple arithmetic problems; it's about developing a strong mathematical foundation for tackling more complex challenges in the future. The seemingly simple act of dividing 13 by 5 unlocks a wealth of mathematical understanding.
Latest Posts
Latest Posts
-
175 C To F
Sep 19, 2025
-
12fl Oz To Ml
Sep 19, 2025
-
75 5 Kg In Pounds
Sep 19, 2025
-
3600 Seconds In Minutes
Sep 19, 2025
-
29 40 As A Percent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 13 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.