29/40 As A Percent
renascent
Sep 19, 2025 · 5 min read
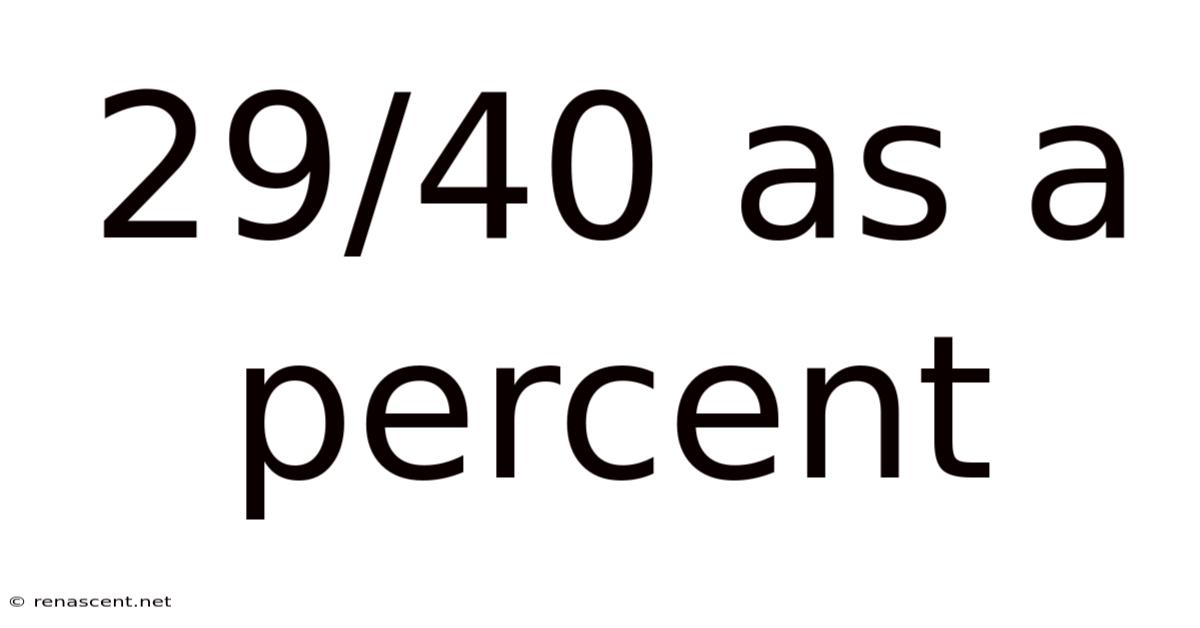
Table of Contents
29/40 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from calculating grades and discounts to understanding financial reports and scientific data. This article provides a comprehensive guide on how to convert the fraction 29/40 into a percentage, exploring different methods, explaining the underlying concepts, and addressing frequently asked questions. Understanding this process empowers you to tackle similar conversions with confidence.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 29/40, 29 is the numerator and 40 is the denominator. This signifies 29 parts out of a total of 40 parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts out of 100 make up the whole. For example, 75% means 75 parts out of 100. Percentages are commonly used to express proportions, rates, and changes.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 29/40 to a percentage is to directly convert the fraction into a decimal and then multiply by 100.
-
Divide the numerator by the denominator: Divide 29 by 40. This calculation results in 0.725.
-
Multiply by 100: Multiply the decimal (0.725) by 100 to express it as a percentage. 0.725 x 100 = 72.5.
-
Add the percentage symbol: Therefore, 29/40 as a percentage is 72.5%.
This method is concise and efficient for simple fraction-to-percentage conversions.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction of 29/40 that has a denominator of 100. This equivalent fraction directly represents the percentage.
-
Determine the scaling factor: To change the denominator from 40 to 100, we need to multiply it by 100/40, which simplifies to 2.5.
-
Apply the scaling factor to both numerator and denominator: Multiply both the numerator (29) and the denominator (40) by 2.5:
- Numerator: 29 x 2.5 = 72.5
- Denominator: 40 x 2.5 = 100
-
Express as a percentage: The resulting equivalent fraction is 72.5/100, which directly translates to 72.5%.
This method provides a clear visualization of the percentage as parts per hundred. However, it might not always be straightforward, especially if the scaling factor involves decimals or isn't a whole number.
Method 3: Using Proportions
Proportions offer a more algebraic approach to converting fractions to percentages. This method involves setting up a proportion that equates the fraction to an unknown percentage over 100.
-
Set up the proportion: Let 'x' represent the unknown percentage. The proportion is:
29/40 = x/100
-
Cross-multiply: Cross-multiply to solve for 'x':
40x = 2900
-
Solve for x: Divide both sides by 40:
x = 2900/40 = 72.5
-
Express as a percentage: Therefore, x = 72.5%.
This method is particularly useful for more complex fraction-to-percentage conversions and demonstrates the relationship between fractions and percentages in a formal mathematical context.
Illustrative Examples: Applying the Conversion
Understanding how to convert 29/40 to a percentage can be applied to various real-world scenarios. Let's look at a few examples:
-
Academic Performance: If a student answered 29 out of 40 questions correctly on a test, their score is 72.5%.
-
Sales Figures: If a salesperson achieved 29 sales out of a target of 40, their performance rate is 72.5%.
-
Discount Calculation: A 29/40 discount on an item implies a 72.5% discount.
These examples highlight the practical utility of converting fractions to percentages in interpreting data and making informed decisions.
Scientific and Technical Applications
Beyond everyday scenarios, converting fractions to percentages is vital in numerous scientific and technical fields.
-
Data Analysis: In statistics and data analysis, representing proportions as percentages facilitates comparison and interpretation of results.
-
Engineering: Percentage calculations are crucial in engineering for calculating tolerances, efficiencies, and error rates.
-
Chemistry: Concentration of solutions is often expressed as percentages (e.g., weight percent, volume percent).
-
Physics: Efficiency of machines or processes is often expressed as a percentage.
Frequently Asked Questions (FAQ)
Q1: Can I round the percentage up or down?
A1: Whether you round depends on the context. In many situations, keeping the decimal (72.5%) provides greater accuracy. However, rounding to 73% might be acceptable if the context allows for a slightly less precise representation.
Q2: What if the fraction has a larger denominator?
A2: The same methods apply, regardless of the denominator's size. You can use any of the three methods discussed above, although the direct division method (Method 1) is often the most efficient for larger denominators.
Q3: What if the fraction is an improper fraction (numerator is larger than the denominator)?
A3: The process remains the same. You'll still divide the numerator by the denominator, resulting in a decimal greater than 1, which you then multiply by 100 to get a percentage greater than 100%.
Q4: Are there any online calculators to perform these conversions?
A4: Yes, many online calculators are available to convert fractions to percentages quickly. These tools can be helpful for verification or for handling more complex calculations.
Conclusion
Converting 29/40 to a percentage, resulting in 72.5%, is a straightforward process that utilizes fundamental mathematical principles. Understanding the different methods—direct conversion, equivalent fractions, and proportions—enables you to approach various fraction-to-percentage conversions with confidence. This skill holds practical value in numerous real-world applications and across multiple disciplines, highlighting its significance in mathematical literacy and problem-solving. The ability to perform these conversions accurately is essential for interpreting data, making informed decisions, and enhancing comprehension across various fields of study and professional settings. Mastering this concept opens doors to a more profound understanding of numerical representation and data analysis.
Latest Posts
Latest Posts
-
15 Divided By 10
Sep 19, 2025
-
Soniq Universal Remote Code
Sep 19, 2025
-
Multiplication By Distributive Property
Sep 19, 2025
-
104 Mph To Km
Sep 19, 2025
-
9 20 As A Percent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 29/40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.