14 Divided By 5
renascent
Sep 16, 2025 · 5 min read
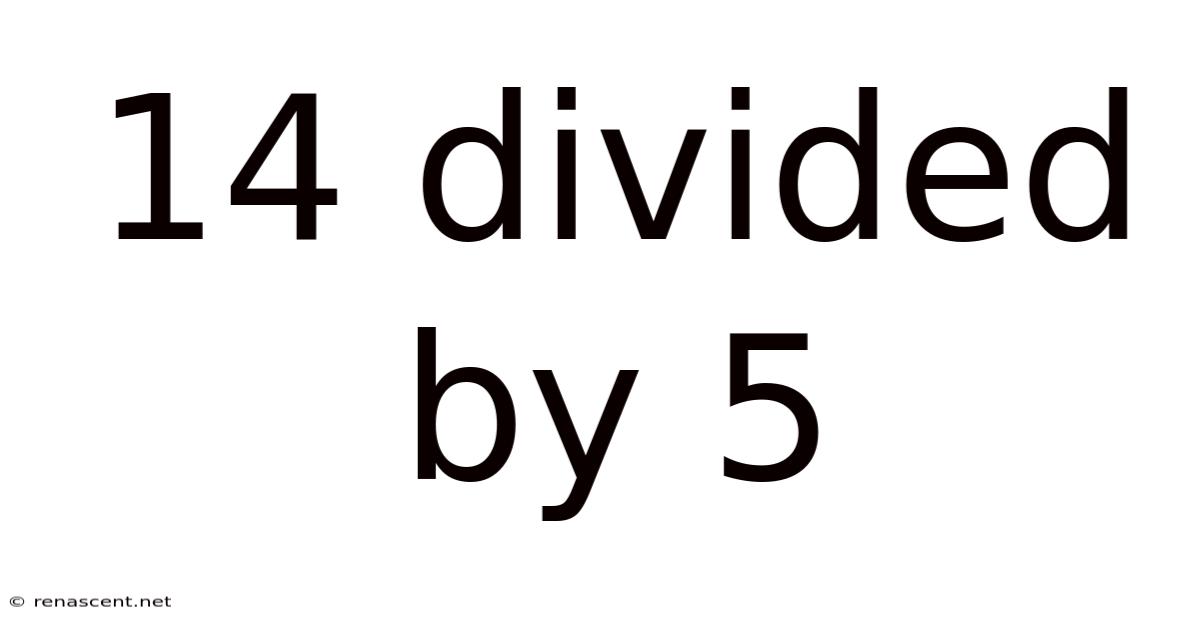
Table of Contents
Unveiling the Mystery: A Deep Dive into 14 Divided by 5
Dividing 14 by 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, a closer look reveals a wealth of mathematical concepts and applications that extend far beyond basic division. This comprehensive guide will explore the different ways to solve 14 ÷ 5, delve into the underlying principles, and illustrate its relevance in various contexts, from everyday life to advanced mathematics. We'll even tackle some common misconceptions and frequently asked questions. By the end, you'll have a thorough understanding of this seemingly straightforward calculation and its broader implications.
Understanding Division: The Foundation
Before we tackle 14 ÷ 5 specifically, let's refresh our understanding of division. Division is fundamentally the process of sharing or grouping a quantity into equal parts. When we divide 14 by 5, we're asking: "If we have 14 items, how many groups of 5 can we make, and how many items will be left over?"
Methods for Solving 14 ÷ 5
There are several ways to approach this division problem, each offering a unique perspective and reinforcing different mathematical concepts.
1. Long Division: The Classic Approach
Long division is a systematic algorithm that breaks down the division process into a series of steps. Here's how it works for 14 ÷ 5:
-
Set up the problem: Write 14 inside the long division symbol (⟌) and 5 outside.
-
Divide: How many times does 5 go into 14? It goes in 2 times (5 x 2 = 10). Write the '2' above the '4' in 14.
-
Multiply: Multiply the quotient (2) by the divisor (5): 2 x 5 = 10.
-
Subtract: Subtract the result (10) from the dividend (14): 14 - 10 = 4.
-
Remainder: The result (4) is the remainder.
Therefore, 14 ÷ 5 = 2 with a remainder of 4.
2. Repeated Subtraction: A Conceptual Approach
This method visually demonstrates the concept of grouping. We repeatedly subtract the divisor (5) from the dividend (14) until we can't subtract any more without going into negative numbers.
- 14 - 5 = 9
- 9 - 5 = 4
We subtracted 5 twice, indicating two groups of 5. The remaining 4 is the remainder. Again, we get 2 with a remainder of 4.
3. Fractions: Expressing the Remainder
Instead of stating a remainder, we can express the result as a mixed number or an improper fraction. The remainder (4) becomes the numerator of a fraction, and the divisor (5) becomes the denominator.
- Mixed Number: 2 ⁴⁄₅ (This reads as "two and four-fifths")
- Improper Fraction: ¹⁴⁄₅ (This represents 14 divided into 5 equal parts)
These fractional representations offer a more precise and complete answer than simply stating the remainder.
Beyond the Basics: Exploring Deeper Concepts
The seemingly simple calculation of 14 ÷ 5 opens doors to more complex mathematical ideas.
1. Decimals: A More Precise Answer
Instead of a remainder or a fraction, we can express the answer as a decimal. To do this, we continue the long division process by adding a decimal point and zeros to the dividend:
- After subtracting 10 from 14, we have a remainder of 4.
- Add a decimal point to the 14 and a zero: 14.0
- Bring down the zero: Now we have 40.
- How many times does 5 go into 40? It goes in 8 times (5 x 8 = 40).
- Subtract 40 from 40, leaving a remainder of 0.
Therefore, 14 ÷ 5 = 2.8
This decimal representation provides a precise answer, eliminating the ambiguity of the remainder.
2. Ratios and Proportions: Real-World Applications
The division of 14 by 5 often appears in ratio and proportion problems. For instance, if you have 14 apples and want to divide them equally among 5 friends, the result (2.8 apples per friend) represents the proportional share each friend receives. While you can't physically divide an apple into 0.8 parts, the decimal representation allows for a precise understanding of the distribution.
3. Modular Arithmetic: Exploring Remainders
Modular arithmetic focuses on the remainders of division. In the context of 14 ÷ 5, the remainder is 4. This is often written as 14 ≡ 4 (mod 5), meaning "14 is congruent to 4 modulo 5". This concept finds applications in cryptography, computer science, and number theory.
Applications in Real-World Scenarios
The division of 14 by 5, while seemingly simple, appears in countless real-world situations:
- Sharing resources: Dividing snacks, toys, or other items equally among a group of people.
- Calculating unit prices: Determining the cost per item when purchasing multiple units.
- Averaging data: Calculating the average score on a test or the average speed of a journey.
- Converting units: Converting larger units (e.g., feet) into smaller units (e.g., inches).
- Scaling recipes: Adjusting ingredient quantities when preparing food for a larger or smaller number of people.
Frequently Asked Questions (FAQ)
Q: Why is there a remainder in 14 ÷ 5?
A: Because 14 is not a multiple of 5. We can make two full groups of 5 from 14, but there are 4 items left over that can't be divided equally into groups of 5.
Q: Is it always necessary to express the remainder as a decimal or fraction?
A: No. The appropriate way to express the answer depends on the context of the problem. A remainder might be perfectly acceptable in some situations, while a decimal or fraction provides more precision in others.
Q: Can negative numbers be involved in division?
A: Yes. Dividing a negative number by a positive number (or vice versa) results in a negative quotient. The rules for signs in division are the same as in multiplication: a positive divided by a positive is positive, a negative divided by a negative is positive, and a positive divided by a negative (or vice versa) is negative.
Conclusion: The Significance of Simplicity
While the division of 14 by 5 may appear trivial at first glance, its underlying principles and applications are far-reaching. This detailed exploration demonstrates how a basic arithmetic operation connects to advanced mathematical concepts and real-world scenarios. Understanding the multiple ways to solve this problem – long division, repeated subtraction, fractions, decimals – solidifies fundamental mathematical skills and broadens our understanding of numbers and their relationships. The seemingly simple act of dividing 14 by 5 unlocks a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Merry Christmas In Thai
Sep 16, 2025
-
Kindle Paperwhite 16 Gb
Sep 16, 2025
-
High Sierra Rolling Backpack
Sep 16, 2025
-
90 C En F
Sep 16, 2025
-
33 40 As A Percent
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 14 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.