15/8 As A Decimal
renascent
Sep 23, 2025 · 5 min read
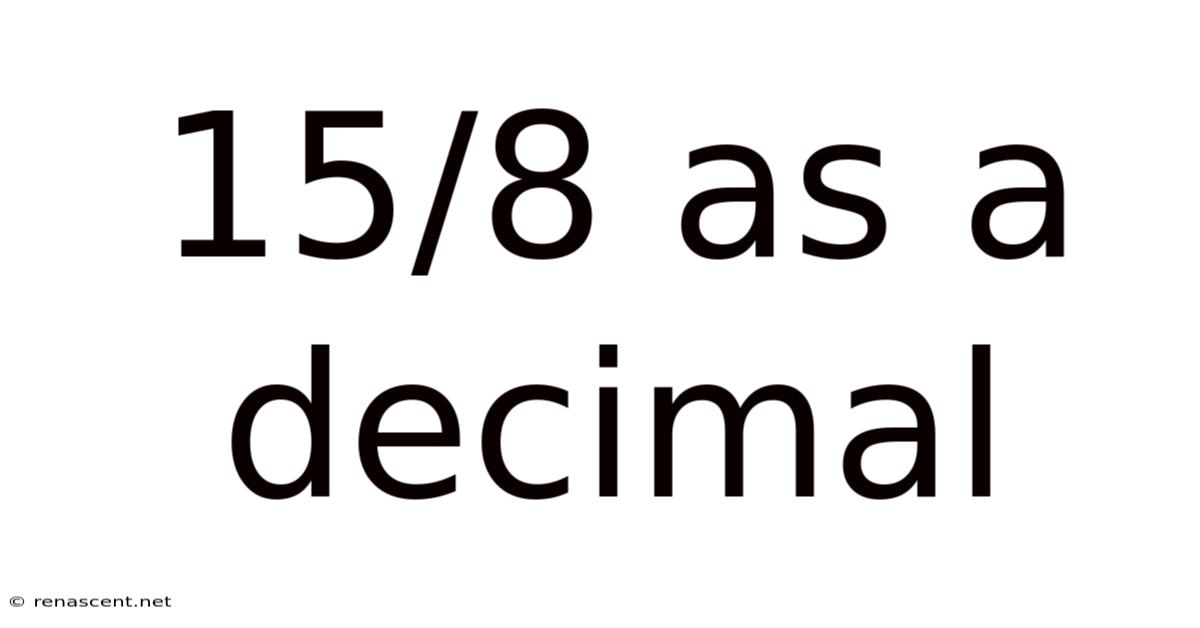
Table of Contents
15/8 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article delves deep into converting the fraction 15/8 into its decimal form, exploring various methods and providing a comprehensive understanding of the underlying concepts. We'll cover different approaches, including long division, and discuss the significance of understanding decimal representations of fractions in various applications. By the end, you'll not only know the decimal equivalent of 15/8 but also have a firm grasp of the principles involved in fraction-to-decimal conversions.
Understanding Fractions and Decimals
Before diving into the conversion of 15/8, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 15/8, 15 is the numerator and 8 is the denominator. This means we have 15 parts out of a total of 8 parts.
A decimal, on the other hand, represents a number based on the powers of 10. Each digit to the right of the decimal point represents a fraction with a denominator that is a power of 10 (10, 100, 1000, and so on). For instance, 0.5 is equivalent to 5/10, and 0.25 is equivalent to 25/100.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (15) by the denominator (8).
- Set up the division: Write 15 as the dividend and 8 as the divisor.
- Divide: 8 goes into 15 one time (8 x 1 = 8). Subtract 8 from 15, leaving a remainder of 7.
- Add a decimal point and a zero: Add a decimal point to the quotient (the result of the division) and add a zero to the remainder (7). This becomes 70.
- Continue dividing: 8 goes into 70 eight times (8 x 8 = 64). Subtract 64 from 70, leaving a remainder of 6.
- Repeat the process: Add another zero to the remainder (6) making it 60. 8 goes into 60 seven times (8 x 7 = 56). Subtract 56 from 60, leaving a remainder of 4.
- Continue until you have reached the desired accuracy or a repeating pattern emerges: Add another zero to the remainder (4) to make it 40. 8 goes into 40 five times (8 x 5 = 40). The remainder is 0, indicating the division is complete.
Therefore, 15/8 = 1.875
Method 2: Converting to an Improper Fraction (if necessary)
If the fraction is an improper fraction (where the numerator is larger than the denominator), as is the case with 15/8, you can convert it to a mixed number first. This makes the long division slightly simpler.
- Divide the numerator by the denominator: 15 divided by 8 is 1 with a remainder of 7.
- Write the mixed number: This gives us the mixed number 1 7/8.
- Convert the fractional part to a decimal: Now, you only need to convert 7/8 to a decimal using long division (as described above). 7 divided by 8 is 0.875.
- Combine the whole number and the decimal: Adding the whole number (1) to the decimal (0.875) gives us 1.875.
Understanding the Decimal Representation
The decimal representation 1.875 provides a clear numerical value for the fraction 15/8. It is important to understand what this decimal represents. 1.875 is equal to one whole unit plus 875 thousandths of a unit. This is a terminating decimal, meaning the decimal representation ends. Not all fractions result in terminating decimals; some result in repeating decimals, where a pattern of digits repeats infinitely.
Practical Applications
Understanding the decimal equivalent of fractions is crucial in many real-world applications:
- Measurement: Many measurements involve fractions (e.g., inches, centimeters). Converting these fractions to decimals is essential for accurate calculations.
- Finance: Calculations involving interest rates, percentages, and monetary amounts often require converting fractions to decimals.
- Science: In scientific calculations, fractions are frequently converted to decimals for easier computations and data analysis.
- Engineering: Engineering designs and calculations frequently use both fractions and decimals, requiring seamless conversion between the two.
- Data Analysis: In statistics and data analysis, converting fractions to decimals simplifies computations and data representation, making the data easier to interpret.
Frequently Asked Questions (FAQs)
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that have prime factors other than 2 and 5 (like 3, 7, 11, etc.) will result in repeating decimals. For example, 1/3 = 0.333...
Q: What if I want to convert a fraction with a larger numerator and denominator?
A: The long division method still applies. The process might take longer, but the principle remains the same. You can use a calculator for larger numbers to speed up the calculation, but understanding the process is critical.
Q: Is there a quicker way to convert simple fractions to decimals?
A: For some common fractions, memorizing their decimal equivalents can be helpful. For example, 1/2 = 0.5, 1/4 = 0.25, 1/8 = 0.125, etc. This can speed up calculations for simpler fractions.
Q: Why is it important to understand both fractions and decimals?
A: Both fractions and decimals are essential representations of numbers. Understanding both and the ability to convert between them allows for greater flexibility and efficiency in various mathematical and real-world applications. Choosing the most appropriate form depends on the context of the problem or calculation.
Conclusion
Converting 15/8 to its decimal equivalent, 1.875, is a straightforward process, readily achievable through long division or by converting it to a mixed number first. Understanding this conversion is not just about getting the answer but also about grasping the fundamental relationship between fractions and decimals. This understanding is critical for success in various fields, from everyday life to advanced mathematical and scientific pursuits. The ability to seamlessly move between fractional and decimal representations empowers you to tackle mathematical problems with greater confidence and efficiency. The methods explained here, coupled with practice, will solidify your understanding and skill in performing these crucial conversions.
Latest Posts
Latest Posts
-
Hydrochloric Acid And Magnesium
Sep 24, 2025
-
25 Divided By 30
Sep 24, 2025
-
37 5 As A Fraction
Sep 24, 2025
-
Answer How Many Triangles
Sep 24, 2025
-
2 Toed Sloth Crossword
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 15/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.