176 Divided By 2
renascent
Sep 16, 2025 · 5 min read
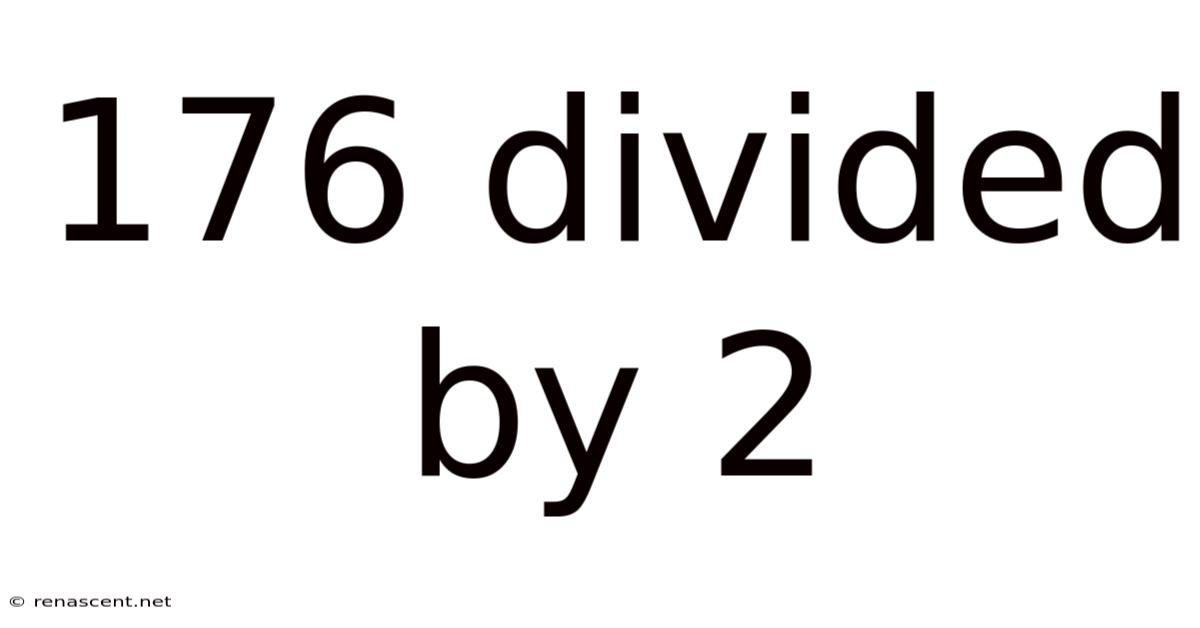
Table of Contents
Unpacking 176 Divided by 2: A Deep Dive into Division
This article explores the seemingly simple calculation of 176 divided by 2, delving beyond the immediate answer to illuminate the underlying principles of division, its various methods, and its practical applications. We'll examine different approaches – from basic arithmetic to visualizing the problem – to solidify your understanding of this fundamental mathematical operation. This comprehensive guide will benefit students of all levels, reinforcing core mathematical concepts and offering diverse strategies for solving similar problems. Understanding division is key to mastering more complex mathematical concepts later on.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the case of 176 divided by 2 (written as 176 ÷ 2 or 176/2), we're asking: "How many times does 2 fit into 176?" The answer, as we'll see in multiple ways, is 88. But the real value lies in grasping how we arrive at this answer and the broader implications of the process.
Method 1: Long Division
Long division is a standard algorithm taught in schools to perform division, especially with larger numbers. Let's apply it to 176 ÷ 2:
-
Set up the problem: Write 176 inside the long division symbol (⟌) and 2 outside.
2⟌176 -
Divide the hundreds digit: 2 goes into 1 zero times, so we move to the tens digit. Consider the first two digits, 17. 2 goes into 17 eight times (8 x 2 = 16). Write the 8 above the 7.
8 2⟌176 -
Subtract and bring down: Subtract 16 from 17, leaving 1. Bring down the next digit, 6, to make 16.
8 2⟌176 -16 16 -
Divide the tens digit: 2 goes into 16 eight times (8 x 2 = 16). Write the 8 above the 6.
88 2⟌176 -16 16 -
Subtract and conclude: Subtract 16 from 16, leaving 0. There is no remainder. The answer is 88.
88 2⟌176 -16 16 -16 0
Therefore, 176 ÷ 2 = 88.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the divisor (2) from the dividend (176) until you reach zero. Each subtraction represents one instance of the divisor fitting into the dividend. While less efficient for large numbers, it visually reinforces the concept of division.
- Start with 176.
- Subtract 2 repeatedly: 176 - 2 = 174; 174 - 2 = 172; and so on.
- Continue this process until you reach 0.
- Count the number of times you subtracted 2. This count will be your answer.
This method is tedious for larger numbers but illustrates the core principle of division—repeated subtraction until exhaustion. While not practical for 176 ÷ 2, it’s a helpful visualization for grasping the fundamental concept.
Method 3: Halving
Since we're dividing by 2, we can simply halve the number 176. This is a quick and efficient method for dividing by 2.
- Halve the hundreds digit: 100 halved is 50.
- Halve the tens digit: 70 halved is 35.
- Halve the units digit: 6 halved is 3.
- Add the halves together: 50 + 35 + 3 = 88
This method leverages the base-ten structure of our number system and provides a streamlined approach for division by 2.
Visualizing Division: The Array Model
Imagine arranging 176 objects into two equal groups. This visual representation helps to understand division concretely. You would distribute the objects, one by one, into two groups until all 176 objects are equally divided. The number of objects in each group would be the result of the division, which is 88. While not practical for such a large number of objects, this model aids in understanding the concept of equal distribution.
Explanation of the Answer: 88
The answer, 88, signifies that if you divide 176 into two equal parts, each part will contain 88 units. This simple result has wider implications in various applications, as we'll explore below.
Real-World Applications
Division, and the specific example of 176 ÷ 2, finds application in countless everyday scenarios:
- Sharing equally: If you have 176 candies to share equally among two friends, each friend receives 88 candies.
- Calculating averages: If you drive 176 miles in 2 hours, your average speed is 88 miles per hour.
- Scaling recipes: If a recipe calls for 176 grams of flour and you want to halve the recipe, you'll need 88 grams of flour.
- Financial calculations: Splitting a bill of $176 between two people results in a cost of $88 per person.
- Geometric problems: If a rectangle has an area of 176 square units and a width of 2 units, its length is 88 units.
These examples showcase the ubiquitous nature of division in problem-solving.
Further Exploration: Dividing by Other Numbers
Understanding the division of 176 by 2 provides a foundation for tackling more complex division problems. The same principles and methods (long division, repeated subtraction, etc.) can be applied when dividing by other numbers. The key is to systematically break down the problem and apply the chosen method consistently.
Frequently Asked Questions (FAQ)
Q: What if there's a remainder when dividing 176 by a number other than 2?
A: If you divide 176 by a number that doesn't divide it evenly, you'll have a remainder. For example, 176 ÷ 3 results in 58 with a remainder of 2 (58 x 3 + 2 = 176). The remainder indicates the portion left over after the equal distribution.
Q: Are there other ways to calculate 176 ÷ 2?
A: Yes, while we've covered several methods, other approaches exist, such as using calculators or specialized software. However, understanding the fundamental methods strengthens your mathematical foundation.
Q: Why is understanding division important?
A: Division is crucial for problem-solving in various fields, including science, engineering, finance, and everyday life. It forms the basis for more advanced mathematical concepts and is essential for critical thinking and analytical skills.
Conclusion: Mastering Division
This detailed exploration of 176 divided by 2 has moved beyond a simple arithmetic problem to illustrate the broader principles of division. By understanding different methods, visualizing the process, and exploring real-world applications, you can solidify your grasp of this fundamental mathematical operation. Remember, the key to mastering division lies not just in obtaining the correct answer but also in comprehending the underlying concepts and their wide-ranging implications. This deeper understanding will serve you well in your future mathematical endeavors.
Latest Posts
Latest Posts
-
2 3as A Percentage
Sep 16, 2025
-
38 8977 N 77 0365 W
Sep 16, 2025
-
27x11 4 Bicycle Tires
Sep 16, 2025
-
1 5 Cm In Mm
Sep 16, 2025
-
Affix As A Patch
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 176 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.